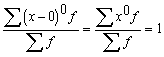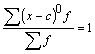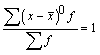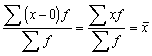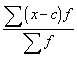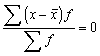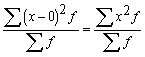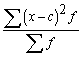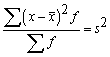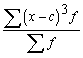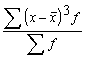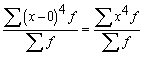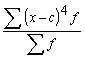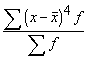1.Empīriskie sadalījumi un to raksturotāji
1.1. Empīriskie sadalījumi un to īpašības
1.1.1.Variācijas rindas
Statistikas
pētījuma objekts vienmēr ir masveida
objekti un parādības, piemēram, kāda uzņēmuma
strādnieki, rajona lauksaimniecības uzņēmumi, visas valsts iedzīvotāji utt.
Tātad statistikas pētījuma objekts ir kopa jeb kopums, ko veido kopas
vienības jeb elementi (cilvēki, uzņēmumi utt.). Lai iegūtu ziņas par
interesējošo kopu, ir jānovēro tās vienības un jāreģistrē dati par svarīgākajām
pazīmēm, kas raksturo kopas vienību un līdz ar to visu kopu. Datu savākšanas
procesu sauc par statistisko novērošanu. Statistiskās novērošanas gaitā parasti
savāc datus par vairākām, nereti daudzām pazīmēm. Tomēr vienkāršākās pētījuma
metodes paredz datus apstrādāt un analizēt par katru pazīmi atsevišķi. Tādēļ
pieņemam, ka par katru kopas vienību ir reģistrēts viens rādītājs, visbiežāk -
skaitlis, kas raksturo vienu novērojamo pazīmi.
Var
novērot visas interesējošās kopas vienības. Šādu kopu sauc par ģenerālkopu
jeb ģenerālo
kopu.
Var novērot tikai kādu ģenerālkopas daļu, kuru atlasa tā, lai tā labi
pārstāvētu (reprezentētu) visu ģenerālkopu. Tā atlasītu kopu sauc par izlasi.
Izlases metode tiks aplūkota turpmākās nodaļās.
Pieņemsim,
ka 10 studentu grupa, kārtojot eksāmenu ir ieguvusi šādas atzīmes (desmit ballu
sistēmā): 7;5;6;9;7;8;3;4;4;7. Tā kā studentu skaits, kuri kārtojuši eksāmenu,
ir neliels, dati ir labi pārskatāmi. Viegli secināt, ka visbiežāk iegūtā atzīme
ir 7 (labi). Maksimālā atzīme ir 9 un minimālā 3. Šādu datu jeb novērojumu
virkni sauc par nesakārtotu empīrisko rindu. Ja studentu skaits būtu vismaz
30…50, nesakārtota datu rinda jau būtu nepārskatāma. Lai uztvertu informāciju,
ko slēpj reģistrētie statistiskie dati, tie ir jāsistematizē, jāizstrādā.
Pirms
uzsākam šo darbu, ir jāiepazīstas ar dažiem statistikā plaši lietotiem
jēdzieniem. Jau minējām kopu jeb kopumu. Piemērā tā ir 10
studentu grupa. Statistikā kopa sastāv no kopas vienībām, piemērā kopas
vienības ir katrs atsevišķs students. Par katru kopas vienību novērojam
(reģistrējam) vienu vai vairākas pazīmes. Piemērā novērojamā pazīme
ir atzīme eksāmenā. Katrai pazīmei var būt ierobežots vai neierobežots skaits nozīmju
jeb variantu.
Piemērā tās ir vērtējuma gradācijas: 10, 9,…, 2, 1. Statistiskajā novērošanā
atsevišķām kopas vienībām reģistrētās pazīmes vērtības veido empīriskos
datus, kurus vairumā gadījumu sauksim par novērojumiem. Piemērā tie ir desmit
iepriekš minētie skaitļi.
Novēroto
un reģistrēto datu dažādību (vienīgi iespējamo vai nosacīti izdalīto variantu
ietvaros) sauc par variāciju. Ja novērojamai pazīmei piemīt šī dažādība
(variācija), pazīmi sauc par variējošu pazīmi. Praktiski ir
nozīme savākt un apstrādāt datus tikai par variējošām pazīmēm.
Pazīmes
variācija var būt kvantitatīva un atributīva. Variācija ir kvantitatīva, ja
variantus var izteikt ar skaitļiem, piemēram, alga, ražība, pašizmaksa.
Variācija ir atributīva, ja variantus var raksturot tikai ar jēdzieniem,
resp., vārdiem, piemēram, tautība, šķirne utt. Kvantitatīva variācija var būt
diskrēta un nepārtraukta. Variācija ir diskrēta, ja varianti ir nošķirti,
parasti veseli skaitļi (cilvēku skaits ģimenē, istabu skaits dzīvoklī, traktoru
skaits saimniecībā). Variācija ir nepārtraukta, ja viens variants no
otra var atšķirties ar lielumu, kas ir pēc patikas mazs. Šādā gadījumā
variantus nodala mērīšanas, svēršanas vai reģistrācijas precizitāte. Tā,
piemēram, ražību divās saimniecībās var uzlūkot par atšķirīgu, ja tā atšķiras
vismaz par 0,1 cnt/ha.
Nesakārtotu
novērojumu rindu apstrādā, sastādot sadalījuma (variācijas) rindu un aprēķinot
statistiskos raksturotājus jeb rādītājus.
Ja datu
maz (piemēram, mazāk par 30), tad variācijas rindu parasti nesastāda, bet
aprēķina statistiskos rādītājus tieši no nesakārtotas empīriskās rindas.
Ja novēroto
datu ir daudz, statistiķis var izvēlēties, kādus apstrādes paņēmienus lietot.
Var vispirms izveidot variācijas rindu. Tā noder tiešai izpētei un
interpretācijai. Pēc variācijas rindas tuvināti var aprēķināt interesējošos
rādītājus. Citos gadījumos variācijas rindu neizveido, bet vajadzīgos
vispārinošos rādītājus aprēķina tieši pēc nesakārtotiem novērojumu datiem.
Izvēli pamato, ņemot vērā pētījuma mērķi un uzdevumus, savākto datu raksturu un
apjomu, lietojamo skaitļošanas tehniku, kā arī citus apsvērumus.
Aplūkosim
variācijas rindas izveidošanu un interpretāciju.
Sadalījuma jeb variācijas
rindu iegūst, saskaitot, cik reizes reģistrēti vienādi varianti. Rezultātus
sakopo tabulā. Tajā uzrāda noteiktā kārtībā sakārtotas pazīmes vērtības jeb
variantus un to biežumus. Ja biežumi izsaka tiešo kopas vienību skaitu, tad tie
ir absolūtie
biežumi. Biežumus var izteikt procentos, visu kopas apjomu pieņemot par
100. Tā iegūst relatīvos biežumus.
Jēdzienus
“sadalījuma rindas” un “variācijas rindas” speciālajā literatūrā bieži uzlūko
par sinonīmiem. Lietderīgāk par variācijas rindām saukt tikai tās rindas, kuras
sakārtotas kvantitatīvas pazīmes augošā vai dilstošā kārtībā, jo tās var
apstrādāt, izmantojot speciālus variācijas pētīšanas paņēmienus. Apstrādājot
atributīvas sadalījuma rindas, daļu šo paņēmienu nevar izmantot.
Sastādot
variācijas rindu, sākotnējos variantus var apvienot intervālos. Tālākā
variācijas rindas apstrādē intervālu centrus bieži uzskata par
jauniem variantiem. Līdz ar to vienā intervālā nonākušos variantus nosacīti
uzskata par vienādiem.
1.1.
tabulā variācijas rinda izveidota, izmantojot nepārtrauktu pazīmi (graudaugu
ražību cnt/ha). Tādēļ ir izveidoti intervāli (skat. tabulas 2.aili), kuru
lielums ir 4 cnt/ha. Tālākajos aprēķinos par jauniem nosacītiem variantiem
parasti pieņem intervālu centrus (skat. 1.1.tabulas 3.aili). Variācijas rindas,
kurās uzrādīti nevis atsevišķi varianti, bet intervāli, sauc par intervālu
variācijas rindām.
Lai nerastos grūtības, kurā intervālā ieskaitīt
kārtējo novērojumu, kurš tieši atbilst intervālu robežām, apakšējo robežu var
uzrādīt ar lielāku precizitāti nekā augšējo robežu (skat. 1.1.tabulas 2.aili).
Ja abas robežas ir uzrādītas ar vienādu precizitāti un nav citas norādes, tad
intervāla apakšējo robežu ir pieņemts
lasīt ar kontekstu “vairāk nekā”, bet
augšējo robežu ar kontekstu “ieskaitot”.
Tabulas
4. un 5.ailēs ir parādīti intervālu absolūtie un relatīvie biežumi- saimniecību
skaits un šis skaits, pārrēķināts procentos. Katra no šīm ailēm kopā ar aili,
kurā norādīti intervāli vai varianti, veido variācijas rindu.
Apstrādājot intervālu
variācijas rindas, jālieto šādi lielumi:
x![]() - pazīmes vismazākā reģistrētā vērtība, bet, ja tā nav
zināma,
- pazīmes vismazākā reģistrētā vērtība, bet, ja tā nav
zināma,
pirmā
intervāla apakšējā robeža, piemērā 10,01 cnt/ha;
x![]() - pazīmes lielākā reģistrētā vērtība vai pēdējā intervāla
augšējā robeža, piemērā
- pazīmes lielākā reģistrētā vērtība vai pēdējā intervāla
augšējā robeža, piemērā
34,0 cnt/ha;
x![]() -x
-x![]() - variācijas amplitūda jeb apjoms, piemērā
- variācijas amplitūda jeb apjoms, piemērā
34-10=24cnt/ha;
x![]() (z) -norādītā intervāla zemākā (apakšējā) robeža, piemērā
(z) -norādītā intervāla zemākā (apakšējā) robeža, piemērā
x![]() (z)=14,01cnt/ha;
(z)=14,01cnt/ha;
x![]() (a)- norādītā intervāla augstākā (augšējā) robeža, piemērā
(a)- norādītā intervāla augstākā (augšējā) robeža, piemērā
x![]() (a)=22,0cnt/ha;
(a)=22,0cnt/ha; ![]()
![]() - intervāla garums1 jeb grupas lielums.
- intervāla garums1 jeb grupas lielums.![]() = x
= x![]() (a)- x
(a)- x![]() (z) , piemērā
(z) , piemērā ![]() =18-14=4 cnt/ha.
=18-14=4 cnt/ha.
___________________
1 Statistikā intervāla garumu sauc arī par intervāla lielumu, intervāla
plašumu, intervāla apjomu.
1.1.tabula
Kādas ekoloģiskās grupas lauksaimniecības uzņēmumu sadalījums pēc graudaugu
ražības
|
Grupas Nr. |
Graudaugu
ražība, cnt/ha |
Saimniecību |
Uzkrātais
saimniecību |
Graudaugu
sējumu platība ha |
|||
|
|
intervāli |
intervālu
centri |
skaits |
relatīvais
biežums (%) |
skaits |
relatīvais
biežums (%) |
(grupu
statistiskais svars) |
|
1 2 3 4 5 6 |
10,01…14,0 14,01…18,0 18,01…22,0 22,01…26,0 26,01…30,0 30,01…34,0 |
12 16 20 24 28 32 |
4 27 47 43 26 8 |
3 17 30 28 17 5 |
4 31 78 121 147 155 |
3 20 50 78 95 100 |
90 720 1350 1260 810 270 |
|
Kopā |
´ |
´ |
155 |
100 |
´ |
´ |
4500 |
Matemātiskajā
statistikā parasti lieto vienāda garuma intervālus, tātad ![]() =
=![]() = … =
= … =![]() . Ekonomiskajā statistikā lieto arī nevienāda garuma intervālus, visbiežāk
tad, ja tie saistīti ar kaut kādiem ekonomiskiem tipiem, kā arī tad, ja vienāda
garuma intervālu rindas malējos intervālos biežumi ir mazi vai parādās tukši
intervāli.
. Ekonomiskajā statistikā lieto arī nevienāda garuma intervālus, visbiežāk
tad, ja tie saistīti ar kaut kādiem ekonomiskiem tipiem, kā arī tad, ja vienāda
garuma intervālu rindas malējos intervālos biežumi ir mazi vai parādās tukši
intervāli.
Ja nav
nakādu citu apsvērumu par vēlamo intervālu garumu, to var aprēķināt, izmantojot
Sterdžesa
formulu:
![]() =
= ![]() , (1.1)
, (1.1)
kur n - visu novērojumu skaits.
Lietojot
šādu intervāla garumu, variācijas rinda iegūst racionālu samēru. Tā nav par
daudz izstiepta un nav arī par daudz saspiesta, tā ka nezūd ieskats par
sadalījuma īpatnībām atsevišķās tās daļās.
Aprēķinot
racionālu intervāla garumu pēc 1.1. tabulas datiem ar Sterdžesa formulu (1.1),
iegūstam
![]() =
=![]() .
.
Intervāla
garumu izdevīgi izvēlēties veselos, aprēķiniem parocīgos skaitļos, vēl labāk,
ja arī intervālu centri iznāk veseli skaitļi. Tādēļ, izveidojot 1.1. tabulu ir
izmantots ![]() .
.
Novērtējot
izveidoto variācijas rindu, secinām, ka visvairāk saimniecību ir ieguvušas
ražību no 18 līdz 26 cnt/ha (vislielākie biežumi ir 3. un4. intervālos, kuri
atrodas sadalījuma vidū). Šāda ražība ir raksturīga dotai ekoloģiskai grupai,
kurā dominē smilts un mālsmilts augsnes. Tajā pat laikā šajā ekoloģiskajā grupā
ir diezgan daudz saimniecību, kuras ieguvušas ievērojami augstāku ražību; ir
arī saimniecības, kurās ražība zemāka. Tās vai nu atrodas īpatnējos dabas
apstākļos, vai arī izmanto saimniecību pamatmasai neraksturīgu agrotehniku.
Statistikā
izmanto arī kumulatīvās jeb uzkrāto biežumu variācijas rindas. Kumulatīvās
variācijas rindas tabulā uzrāda variantus, resp., intervālus un
uzkrātos biežumus. Tajos ieskaita visas tās kopas vienības, kurām reģistrētā
pētāmās pazīmes vērtība ir mazāka vai vienāda ar attiecīgā intervāla augšējo
robežu. Kumulatīvās variācijas rindas izveidošana ir parādīta 1.1. tabulas 6.
un 7. ailēs.
Variācijas
rinda izveidojas datu grupēšanas rezultātā. Grupēšana ir viena no
statistisko datu apstrādes pamatmetodēm. Gandrīz katra grupējuma tabula satur
variācijas rindu, bet parasti grupējuma tabulās ir rādītāji ne tikai par vienu,
bet par divām vai vairākām pazīmēm. Tāpēc grupējumu tabulas pēc satura mēdz būt
plašākas, piem., 1.1. tabulas pēdējā aile.
Statistiskās
kopas vienības var sagrupēt ne vien pēc kvantitatīvas, bet arī pēc atributīvas
pazīmes. Uzrādot tabulā vienību skaitu katrā izdalītajā grupā, iegūst atributīvu
sadalījuma rindu.
Plašāk
izpētīts un lietots ir atributīvās variācijas speciāls gadījums - alternatīvā
variācija. Par alternatīvo variāciju runā tad, ja pazīme var iegūt tikai
divas nozīmes, resp., ir iespējami tikai divi varianti, piemēram, vīrietis vai
sieviete; strādājošais ar augstāko izglītību vai bez tās utt.
1.1.2. Variācijas rindu grafiskie attēli
Variācijas
rindu grafiskie attēli padara uzskatāmāku pētāmās kopas sadalījumu pēc
interesējošās pazīmes. Variācijas rindu var attēlot ar poligonu vai
histogrammu, bet kumulatīvo rindu- ar kumulātu.
Poligonu
izmanto galvenokārt diskrētu variācijas rindu attēlošanai. To izveido šādi: uz
abscisu ass atliek attēlojamos variantus (pazīmes vērtības). Šajos punktos
konstruē abscisu asij perpendikulārus taisnes nogriežņus, kuru garumi ir
proporcionāli variantu biežumiem. Pēc tam blakus esošo nogriežņu virsotnes
savieno ar taisnes nogriežņiem un iegūst
poligonu. Var rīkoties arī citādi. Koordinātu sistēmā atliek punktus, kuru
koordinātas attiecīgi ir pazīmes vērtības (varianti) un to biežumi. Pēc tam,
blakus esošos punktus savienojot ar taisnes nogriežņiem, iegūst poligonu.
Histogrammu lieto
galvenokārt intervālu variācijas rindu attēlošanai. Uz abscisu ass atliek
nogriežņus, kas atbilst variācijas rindas intervāliem. Pieņemot tos par
pamatiem, konstruē taisnstūrus, kuru augstumi ir proporcionāli variantu
biežumiem. Var izmantot kā absolūtos, tā relatīvos biežumus. Šādi attēlo
vienāda garuma intervālu variācijas rindu.
Par
intervāla blīvumu sauc intervāla biežuma attiecību pret intervāla
garumu. Intervāla blīvums raksturo kopas vienību skaitu, rēķinot uz vienu
variējošās pazīmes vienību.
Histogramma,
kas attēlo 1.1. tabulas datus, ir parādīta 1.1. grafiskajā attēlā.
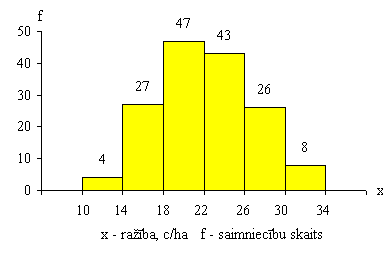
1.1.
attēls. Lauksiamniecības uzņēmumu sadalījums pēc graudaugu ražības.
Kumulātu
iegūst, attēlojot kumulatīvo variācijas rindu. Koordinātu sistēmā atliek
punktus, kuru abscisas ir proporcionālas variantu lielumiem, bet ordinātas -
attiecīgo variantu uzkrātajiem biežumiem (absolūtajiem vai relatīvajiem).
Savienojot blakus esošos punktus ar taisnes nogriežņiem, iegūst lauztu līniju -
kumulātu.
Ja ir
jāattēlo intervālu variācijas rinda, par pirmā intervāla apakšējās robežas
ordinātu ņem nulli, bet par augšējās robežas ordinātu - pirmā intervāla
biežumu. Par otrā intervāla augšējās robežas ordinātu ņem otrā intervāla
uzkrāto biežumu utt. Par pēdējā intervāla augšējās robežas ordinātu jāņem viss
kopas apjoms (absolūto vai relatīvo biežumu summa).
Kumulāta,
kas attēlo 1.1. tabulas datus (absolūtos biežumus), ir parādīta 1.2. attēlā.
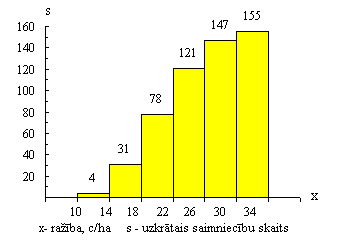
1.2.
attēls. Lauksaimniecības uzņēmumu sadalījums pēc graudaugu ražības.
1.1.3. Variācijas rindas raksturotāji
Variācijas
rinda un tās grafiskais attēls dod izvērstu ieskatu par pētāmās kopas īpašībām.
Taču šāda informācija ne vienmēr ir pietiekama - īpaši tad, ja ir jāsalīdzina
divi vai vairāki sadalījumi. Bez tam variācijas rindas un to attēli aizņem
samērā daudz vietas statistikas materiālos, tajās nav pietiekami augsts
informācijas blīvums. Tādēļ statistikā izmanto rādītājus, kuri īsi un
koncentrēti raksturo pašas galvenās sadalījuma īpašības.
Lai
noskaidrotu, kādas sadalījuma īpašības vajadzētu raksturot šiem rādītājiem,
aplūkosim divus sadalījumus, kas doti 1.2. tabulā un 1.3.attēlā. Tur parādītas
divas variācijas rindas: divu ekoloģisko grupu saimniecību sadalījumi pēc
graudaugu ražības.
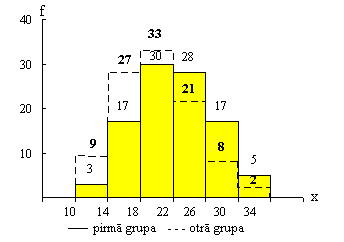
1.3.
attēls. Divu ekoloģisko grupu lauksaimniecības uzņēmumu sadalījumi
pēc graudaugu ražības, procentos.
Salīdzinot
abus sadalījumus, ievērojam šādas atšķirības.
1. Kaut
gan abu sadalījumu centrālie intervāli sakrīt, pirmās ekoloģiskās grupas
sadalījumā lielāki biežumi ir pa labi, bet otrās ekoloģiskās grupas sadalījumā
- pa kreisi no centrālā intervāla. Ja abu sadalījumu novietojumu uz skaitļu ass
novērtē nevis pēc centrālā intervāla, bet pēc visiem intervāliem, tad pirmais
sadalījums ir novirzīts vairāk pa labi lielāku skaitļu apgabalā, bet otrais pa
kreisi - mazāku skaitļu apgabalā.Tādēļ ir vajadzīgs viens vai vairāki rādītāji,
kas raksturo sadalījumu novietojumu uz skaitļu ass. Šim nolūkam noder t.s. lokācijas
rādītāji. Sadalījuma lokāciju raksturo dažādi vidējie lielumi. Parasti
tos sauc par sadalījuma centrālās tendences rādītājiem. Pēdējais apzīmējums
ir piemērots tad, ja sadalījumam ir viens variants ar vislielāko biežumu un tas
atrodas centrā. Bet, ja tādi varianti ir divi vai vairāki un tie neatrodas
blakus, tad vienas centrālās tandences nav. Tomēr paliek sadalījuma lokācija
jeb novietojums. Līdz ar to pēdējais termins ir pēc satura plašāks nekā termins
“centrālā tendence”.
2.
Sadalījumi var atšķirties ar apgabalu, ko tie aizņem uz horizontālās x ass.
Piemērā vizuāli izskatās, ka šie apgabali ir vienādi vai līdzīgi, bet citos
gadījumos tas tā nav. Līdz ar to otrai variācijas rindu raksturotāju grupai
vajadzētu raksturot sadalījumu variāciju. Pie otrās grupas pieder tādi rādītāji
kā variācijas
apjoms jeb amplitūda, vidējā absolūtā novirze, standartnovirze jeb
vidējā kvadrātiskā novirze, variācijas koeficients u.c.
3.
Sadalījumi atšķiras ar savām simetrijas īpašībām.Piemērā abiem sadalījumiem ir
nedaudz izstiepts labais, bet aprauts kreisais zars, turklāt otrajam
sadalījumam šī īpašība ir izteiktāka. Tādēļ ir vajadzīgi rādītāji, kas raksturo
variācijas rindas asimetriju.
1.2. tabula
Graudaugu ražība divu ekoloģisko grupu lauksaimniecības uzņēmumos
|
Grupas
nr. |
Graudaugu
ražība cnt/ha |
Saimniecību
skaits ekoloģiskajās grupās |
Saimniecību
relatīvie biežumi ekoloģiskajās grupās (%) |
Grupu
statistiskie svari pēc graudaugu sējumu platības (%) |
||||
|
|
intervāli |
intervālu
centri |
pirmajā |
otrajā |
pirmajā |
otrajā |
pirmajā |
otrajā |
|
1 2 3 4 5 6 |
10,01…14,0 14,01…18,0 18,01…22,0 22,01…26,0 26,01…30,0 30,01…34,0 |
12 16 20 24 28 32 |
4 27 47 43 26 8 |
17 48 60 37 15 3 |
3 17 30 28 17 5 |
9 27 33 21 8 2 |
2 16 30 28 18 6 |
10 25 32 22 9 2 |
|
Kopā |
´ |
´ |
155 |
180 |
100 |
100 |
100 |
100 |
4.
Otrās ekoloģiskās grupas saimniecību sadalījums (vismaz centrā) paceļas stāvāk
virs horizontālās x ass, veidojot smailāku virsotni. Pirmās ekoloģiskās grupas
saimniecību sadalījums veido lēzenāku figūru. Sadalījuma smailumu sauc par ekscesu.
Ja ir
četri rādītāji, no kuriem viens raksturo variācijas rindas centrālo tendenci,
bet pārējie - variāciju, asimetriju un ekscesu, tad variācijas rinda ir
raksturota samērā pilnīgi. Bieži pietiek jau ar pirmajiem diviem sadalījuma
raksturotājiem (centrālās tendences un variācijas rādītājiem).
Zinot,
ka katru variācijas rindu var raksturot ar četrām īpašībām (centrālo tendenci,
variāciju, asimetriju, ekscesu), var aprēķināt šīs īpašības raksturojošos
rādītājus tieši pēc sākotnējiem datiem. Pašu variācijas rindu tabulas veidā
šādā gadījumā vispār neizstrādā; nav redzams arī tās attēls. Tomēr pēc
aprēķinātajiem raksturotājiem var diezgan labi iedomāties, kāda būtu variācijas
rinda, ja to izveidotu.
Statistisko
raksturotāju aprēķināšana tieši pēc sākotnējiem datiem ir ļoti izdevīga, ja
datus apstrādā ar datortehniku. Tas dod iespēju gandrīz pilnīgi standartizēt
skaitļošanas darbu. Bez tam pēc sākotnējiem datiem aprēķinātie raksturotāji ir
precīzāki nekā pēc iepriekš grupētiem datiem aprēķinātie.
Precizitāte
vairāk zūd tad, ja ir izmantots nedaudz intervālu(variantu). Ja intervālu
daudz, precizitātes zudums mazāks.
Vēl
jāatzīmē, ka ar statistiskajiem raksturotājiem mēs nepētām grupējuma rezultātā
iegūtās variācijas rindas (tabulas) vai tās grafiskā attēla īpašības, kaut arī
tāda raksturotāju interpretācija ir ļoti labi uzskatāma. Tiklab variācijas
rinda kā grupējuma rezultāts, kā arī statistiskie raksturotāji atspoguļo paša
statistiskā objekta (parādības) objektīvās īpašības - objektīvo vienību
sadalījumu, ievērojot šo vienību dažādību. Tādēļ tiklab variācijas rinda
(tabula), kā arī dažādie sadalījuma raksturotāji atspoguļo paša statistiskā
objekta (kopas, kopuma) īpašības. Dažādus raksturotājus, piemēram, vidējos
lielumus, var izmantot neatkarīgi no tā, vai vienlaikus izmanto, vai nē citus
raksturotājus un metodes (grupējumu, grafisko analīzi u.c.). Metožu un rādītāju
kompleksa izmantošana vienīgi padziļina to izpratni.
1.2. Vidējie lielumi un to īpašības
1.2.1. Vidējo lielumu nozīme un veidi
Vidējie
lielumi atklāj masveida parādību raksturīgos līmeņus. Ja statistiskie dati ir
sakopoti, izveidojot variācijas rindu, vidējais lielums raksturo to centrālo
tendenci jeb novietojumu uz 0x ass (grafiskajā attēlā tas ir punkts uz abscisu
ass).
Statistikā
izšķir vairākus vidējo lielumu tipus, kurus var apvienot grupās. Pirmo un
svarīgāko grupu veido pakāpju vidējie: aritmētiskais
vidējais, harmoniskais vidējais, kvadrātiskais vidējais, ģeometriskais vidējais
un citi. Otra svarīgākā grupa ir struktūras vidējie: moda un
mediāna.
Vidējos
lielumus nevar izvēlēties patvaļīgi. Katram vidējam lielumam ir savs saturs un
īpašības, tādēļ to lietošana ir jāpamato, vadoties no pētijuma mērķa un
uzdevumiem, kā arī apstrādājamās informācijas īpatnībām. Lai varētu izvēlēties
vispiemērotāko vidējo, jāzina vidējo lielumu īpašības.
Izšķir
vienkāršos jeb nesvērtos vidējos un svērtos vidējos.
Nesvērtos
vidējos lieto vienmēr, ja ir jāaprēķina nesagrupētu absolūto
lielumu vidējie. Citu lielumu, piemēram, relatīvo lielumu vidējos var
rēķināt kā nesvērtos tikai tad, ja visas kopas vienības no pētāmās pazīmes
veidošanās viedokļa ir vienādi lielas.
Svērtos
vidējos galvenokārt lieto, rēķinot relatīvo (un citu
atvasināto) lielumu vidējos pie kam kopas vienības, vadoties pēc kādas
pētījumam nozīmīgas pazīmes, ir dažāda lieluma.
1.2.2. Pakāpju vidējie
Par pakāpju vidējiem sauc
vidējos, kurus aprēķina, izmantojot šādas formulas. Vienkāršajiem vidējiem:
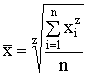 , (1.2.)
, (1.2.)
svērtajiem vidējiem:
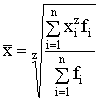 , (1.3)
, (1.3)
kur xi - i-tais novērojums (dats), bet,
rēķinot variācijas rindas vidējo, -variants; n - kopas vienību skaits; fi
- i-tās kopas vienības, bet, rēķinot sagrupētas variācijas rindas vidējo,
varianta statistiskais svars;
z -
pakāpes rādītājs, kas katram vidējā tipam ir atšķirīgs. Biežāk izmantotie
pakāpju rādītāji ir šādi:
-1
- harmoniskais vidējais;
0 - ģeometriskais vidējais;
1 - aritmētiskais vidējais;
2 - kvadrātiskais vidējais utt.
Formulas,
kuras izmanto praktiskos aprēķinos, iegūst, aizstājot iepriekš minētajās
formulās pakāpes rādītāju z ar
vajadzīgo skaitli un izdarot nepieciešamos pārveidojumus.
1.2.3. Aritmētiskais vidējais
Aritmētisko
vidējo iegūst, pakāpju vidējā formulā ņemot z=1. Tā kā x1=x
un ![]() =x, tad vienkāršais aritmētiskais vidējais
ir
=x, tad vienkāršais aritmētiskais vidējais
ir
![]() ; (1.4)
; (1.4)
bet svērtais 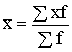 . (1.5)
. (1.5)
Ja
summēšanu izdara pa visu statistisko kopu, summēšanas robežas var neuzrādīt.
Tātad ![]() . Ja summē tikai pa kādu kopas daļu, summēšanas robežas ir
jāuzrāda.
. Ja summē tikai pa kādu kopas daļu, summēšanas robežas ir
jāuzrāda.
Aprēķinot
absolūto
lielumu vidējo pēc nesagrupētiem datiem, vienmēr ir jālieto vienkāršais
aritmētiskais vidējais. Absolūtie lielumi paši par sevi raksturo katra
novērojuma lielumu(masu) statistiskā objekta jeb parādības kopējā apjoma
veidošanā. Tādēļ kādi citi samērotāji statistisko svaru veidā nav vajadzīgi.
Piemērs.
Aprēķināt vidējo mēneša darba algu 8 cilvēku brigādei, ja atsevišķiem brigādes
strādniekiem šajā mēnesī ir izmaksāts: 215,27; 230,91; 190,15; 250,31; 201,50;
222,93; 219,10; 205,12 lati.
Šajā
gadījumā ir jārēķina individuālu absolūto lielumu vidējais. Mūsu rīcībā ir
tieši, nesagrupēti dati par katra strādnieka algu. Tādēļ ir jālieto vienkāršā
(nesvērtā) aritmētiskā vidējā formula. Vienkāršā aritmētiskā vidējā
lietošanas pamatojumu vēl var pastiprināt, ņemot vērā, ka visu strādnieku dati
ir vienādi informatīvi vidējā lieluma veidošanā, kā arī zinot, ka ![]() ir visiem strādniekiem
izmaksātās naudas summa, tātad lielums ar reālu ekonomisku saturu.
ir visiem strādniekiem
izmaksātās naudas summa, tātad lielums ar reālu ekonomisku saturu.
Izdarot
aprēķinus
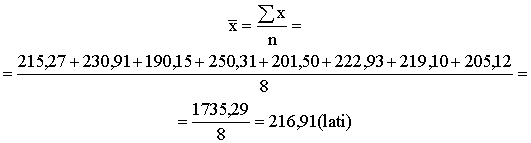
Strādnieka
vidējā mēneša alga pēc noapaļošanas ir 217 lati.
1.2.4. Svērtā aritmētiskā vidējā lietošana
Svērto
aritmētisko vidējo visbiežāk lieto, aprēķinot relatīvo lielumu vidējo. Tāpat
statistiskie svari ir jālieto aprēķinot kopējo vidējo no grupu vidējiem un
dažos citos gadījumos. Ir lietderīgi izšķirt trīs uzdevumu grupas, kuru
ietvaros lieto svērtos vidējos.
Pie
pirmās grupas pieskaitīsim tos uzdevumus, kur, vadoties no
kvalitatīviem (profesionāliem) apsvērumiem, visas statistiskā objekta vienības
nav vienādi lielas (nozīmīgas, informatīvas) vidējā lieluma veidošanā. Pati
pazīme x, kuras vidējais ir jāaprēķina, neraksturo šo lielumu. Piemēram, ja x
ir intensitātes relatīvais lielums.
Piemērs. Aprēķināt iedzīvotāju vidējo
blīvumu trīs Baltijas valstīs, ja ir zināmi dati par katru no tām: Latvijā
39,0, Lietuvā 56,8, Igaunijā 32,7 cilvēki uz km2 (deviņdesmito gadu
vidū).
Rēķinot
vienkāršo aritmētisko vidējo, rezultāts 42,8 ir neprecīzs, jo, vadoties no
pētījamās pazīmes, visas valstis nav vienādi lielas. Pareizus rezultātus šajā
gadījumā dod svērtā aritmētiskā vidējā
formula. Par x tajā jāņem iedzīvotāju skaits uz km2 katrā valstī,
bet par f - valstu teritorijas platība t.km2. Tādēļ papildus
uzdevuma datiem ir jānoskaidro šī platība: Latvijā 64,6, Lietuvā 65,3, Igaunijā
45,2 tūkst.km2.
Līdz ar
to
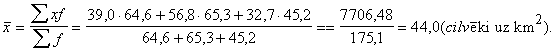
Ja
pazīme x, kurai rēķina aritmētisko vidējo, ir relatīvais lielums, piemērā -
intensitātes relatīvais lielums (iedzīvotāju blīvums), tad reizinājums xf un
arī summa ![]() ir absolūtie lielumi,
piemērā - iedzīvotāju skaits katrā valstī un visās trīs valstīs kopā. Piemērs
parāda, ka pareizi izvēloties statistiskos svarus, ir jānodrošina lai lielumiem
xf un
ir absolūtie lielumi,
piemērā - iedzīvotāju skaits katrā valstī un visās trīs valstīs kopā. Piemērs
parāda, ka pareizi izvēloties statistiskos svarus, ir jānodrošina lai lielumiem
xf un ![]() būtu reāls statistisks saturs un tie būtu izšķiroši pētāmās
problēmas izpētē.
būtu reāls statistisks saturs un tie būtu izšķiroši pētāmās
problēmas izpētē.
Statistiskās
novērošanas un sakopošanas gaitā vispirms iegūst absolūtos lielumus, bet
relatīvos aprēķina vēlāk. Piemēra ietvaros par katru valsti vispirms nosaka
iedzīvotāju skaitu xf un teritorijas platību f, no kā viegli iegūt vajadzīgās
summas ![]() un
un ![]() . Iedzīvotāju blīvumi x var palikt pat neizrēķināti vai
nepublicēti. Vajadzīgo vidējo lielumu (vidējo iedzīvotāju blīvumu) var iegūt
dalot vienu summāro absolūto lielumu ar otru, tātad kā jaunu intensitātes
relatīvo lielumu. Tikai interpretācijas stadijā viņam tiek piešķirts vidējā
lieluma saturs. Līdz ar to ir redzams, ka aritmētiskie vidējie lielumi un
intensitātes relatīvie lielumi ir savā starpā ļoti cieši saistīti rādītāji.
. Iedzīvotāju blīvumi x var palikt pat neizrēķināti vai
nepublicēti. Vajadzīgo vidējo lielumu (vidējo iedzīvotāju blīvumu) var iegūt
dalot vienu summāro absolūto lielumu ar otru, tātad kā jaunu intensitātes
relatīvo lielumu. Tikai interpretācijas stadijā viņam tiek piešķirts vidējā
lieluma saturs. Līdz ar to ir redzams, ka aritmētiskie vidējie lielumi un
intensitātes relatīvie lielumi ir savā starpā ļoti cieši saistīti rādītāji.
Ja,
rēķinot svērto aritmētisko vidējo, par statistiskajiem svariem nav pamatoti
ņemt variantu atkārtošanās reižu skaitu, bet ir jāņem kāda cita pazīme (kura ir
atšķirīga no x), svērtais aritmētiskais vidējais ir teorētiski vienīgais, kurš
dod pareizu un precīzu vidējo, vadoties no uzdevuma profesionālās nostādnes.
Vienkāršais vidējais šādā gadījumā dod tikai tuvinātu rezultātu.
Pie otrās
grupas pieskaitīsim tos uzdevumus, kur vadoties no profesionāliem apsvērumiem
visas kopas vienības ir vienādi lielas (nozīmīgas) vidējā lieluma veidošanā un
pazīme x, kurai vidējais jārēķina, ir diskrēta. Tādā gadījumā skaitliski
identiskus rezultātus iegūstam: 1) aprēķinot nesvērto vidējo pēc sākotnējiem,
nesagrupētiem datiem un 2) aprēķinot svērto aritmētisko vidējo pēc grupētiem
datiem, par statistiskajiem svariem ņemot vienību skaitu katrā grupā.
Piemērs. Aprēķināt vidējo atzīmi 10
studentu grupai, kuras eksaminācijas rezultāti ir šādi: 7;5;6;9;7;8;3;4;4;7
(dati bija jau nodaļas sākumā).
Uzdevuma
atrisināšanai pēc brīvas izvēles var izmantot gan vienkāršā, gan svērtā
aritmētiskā vidējā formulu. Lietojot vienkāršā vidējā formulu, par summējamiem
lielumiem x jāņem visas iegūtās atzīmes (novērtējumi) :
![]() .
.
Lai
izmantotu svērtā aritmētiskā vidējā formulu, par x jāņem diskrētā vērtējuma
varianti: 9; 8; …; 3, Jāsaskaita viņu atkārtošanās reižu skaits, to izmantojot
par statistiskajiem svariem f. Ja variantu atkārtošanās reižu skaits ir
saskaitīts, viegli uzrakstīt variācijas rindu. Tādēļ var uzskatīt, ka pirms
vidējā lieluma rēķināšanas ir izdarīts statistisks grupējums.
|
x |
f |
|
9 8 7 6 5 4 3 |
1 1 3 1 1 2 1 |
|
|
10 |
Līdz ar to
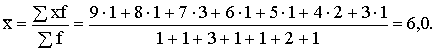
Izteiksmes
skaitītāju parasti aprēķina grupējuma tabulā, tajā papildus izveidojot aili xf.
Abu
formulu lietošana šajā gadījumā dod identiskus rezultātus tādēļ, ka svērtā
aritmētiskā vidējā formulā vienādu novērojumu (datu) tieša saskaitīšana tiek
aizstāta ar reizināšanu.
Praktiski
ieteicamās formulas izvēli nosaka tikai skaitļošanas darba ekonomija. Svērtā
aritmētiskā vidējā lietošana ir efektīva tad, ja: 1) iepriekš ir izstrādāta
diskrēta variācijas rinda vai tā jāizstrādā neatkarīgi no vidējā lieluma
aprēķina; 2) variantu skaits ir daudzkārt mazāks par novērojumu skaitu, un
darbu izpilda ar neprogrammējamu skaitļošanas tehniku. Vienkāršā aritmētiskā
vidējā formula ir efektīva ja: 1) variantu skaits ir liels, resp., tuvs visu
novērojumu skaitam; 2) sākotnējie dati ir fiksēti uz informācijas tehniska
nesēja un skaitļošanu veic ar datoru.
Otrās
uzdevumu grupas ietvaros dažkārt arī diskrētu absolūto lielumu aritmētisko
vidējo ir lietderīgi aprēķināt kā svērto, ja vienādi absolūtie lielumi
daudzkārt atkārtojas.
Pie trešās
grupas pieskaitīsim uzdevumus, kad aritmētiskais vidējais jāaprēķina pēc
intervālu variācijas rindas. Sākotnējie dati nav pieejami vai arī tos grūti
atkārtoti apstrādāt tehnisku iemeslu dēļ. Pēc intervālu variācijas rindas
vidējo aritmētisko vienmēr aprēķina kā svērto. Grupas ietvaros var izšķirt
četras uzdevumu apakšgrupas, atkarībā no tā, kā izpildās zināmi
priekšnosacījumi.
1. Par
visām grupām(intervāliem) ir zināmi tās pazīmes x, kuras vidējais jārēķina,
grupas vidējie lielumi. Izmantojot par variantiem grupu vidējos, saglabājam
kopējā vidējā precizitāti.
2. Grupu
vidējie nav zināmi; par to tuvinātām vērtībām pieņem intervālu centrus. Tādas
aizvietošanas rezultātā kopējā vidējā precizitāte samazinās, turklāt vairāk, ja
grupu maz un sadalījums nav simetrisks.
3.
Vadoties no profesionāliem apsvērumiem, grupu lielumu tieši raksturo vienību
skaits tajās vai arī ir zināmi citi grupu statistiskie svari, kuri precīzi
raksturo grupu lielumu. Tad statistiskās svēršanas rezultātā vidējā precizitāte
nesamazinās.
4.
Prienoteikums 3. nav izpildāms. Par statistiskajiem svariem ir jāizmanto grupu
absolūtie vai relatīvie biežumi, kaut gan tie tikai tuvināti raksturo grupu
lielumu vidējā veidošanās procesā. Kopējā vidējā precizitāte tā rezultātā
samazinās.
Aprēķinātais
vidējais ir maksimāli precīzs, ja vienlaikus izpildas pirmais un trešais
priekšnoteikums. Neprecizitāte var būt vislielākā, ja tie vienlaikus
neizpildās, t.i. uzdevums vienlaikus attiecināms uz 2. un 4. apakšgrupām.
Piemērs.
Aprēķināt pirmās ekoloģiskās grupas laukssaimniecības uzņēmumu vidējo graudaugu
ražību pēc datiem, kas doti 1.1. tabulā.
Šajā
gadījumā ir dota intervālu variācijas rinda, neuzrādot intervālu (grupu)
vidējos. Grupu vidējo vietā kā to tuvinātas vērtības ir jāņem intervālu centri.
Tā rezultātā nedaudz zaudējam kopējā vidējā precizitāti.
Par
grupu statistiskajiem svariem varētu izmantot absolūtos vai relatīvos biežumus
(saimniecību skaitu vai to īpatsvaru procentos). Bet piemērā tabulā ir doti
dati arī par graudaugu sējumu platību katrā grupā (pēdējā aile). Šie lielumi ir
pareizāki grupu statistiskie svari kopējās vidējās ražības veidošanas procesā
nekā saimniecību skaits, tādēļ viņu lietošana dos precīzāku svērto vidējo.
Graudaugu absolūtās sējumu platības vietā var izmantot sējumu platības
struktūru pa grupām procentos, kas aprēķinu precizitāti nesamazina, bet padara
tos ērtākus, jo statistisko svaru summa 100 ir aprēķiniem parocīgāks skaitlis.
Aprēķinus var sakārtot tā, kā tas parādīts 1.7.tabulas pirmajās trīs ailēs(par
statistiskajiem svariem ir izmantota sējumu platība procentos).
Tādējādi
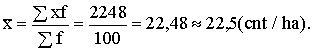
Tātad
vidējā graudaugu ražība pirmās ekoloģiskās grupas saimniecībās bija 22,5cnt/ha.
Tāpat aprēķinot vidējo ražību otras ekoloģiskās grupas saimniecībās(1.1. un
1.2. tabula) iegūstam 20,0 cnt/ha. Starpība 2,5 cnt/ha raksturo abu statistisko
kopu centrālās tendences atšķirību.
Aritmētisko
vidējo grafiski attēlo punkts uz skaitļu ass x, virs kuras paceļas variācijas
rindas histogramma, skat.1.3.attēlu. Histogrammai 1. tāds punkts ir 22,5, bet
histogrammai 2. - 20,0. Šie punkti grafiski nozīmē atbilstošo histogrammu
novietojumu centrus (lokāciju) uz skaitļu ass. Attālums starp šiem diviem
punktiem, salīdzināmo vidējo starpība, (piemērā 22,5 - 20,0=2,5cnt/ha) vislabāk
raksturo pētītās pazīmes atšķirību salīdzimāmajās kopās. Tātad pirmās
ekoloģiskās grupas saimniecībās iegūta par 2,5cnt/ha augstāka graudaugu ražība
nekā otras grupas saimniecībās.
Piemēra
ietvaros vidējo ražību varētu precizēt, ja mūsu rīcībā būtu sākotnējie dati par
graudaugu ražību un sējumu platību katrā saimniecībā. Tad aritmētisko vidējo
varētu aprēķināt par x ņemot katras saimniecības faktisko ražību, bet par f -
sējumu platību. Darba tabulā būtu 155 rindas (atbilsoši saimniecību skaitam) un
kopsummas rinda. Strādājot ar datoru, tādus starprezultātus fiksē tikai mašīnas
atmiņā.
Vēl
labāk, ja mūsu rīcībā būtu dati par graudu kopražu un sējumu platību katrā
saimniecībā. Tos summējot un izdalot kopražas kopsummu ar sējumu platības
kopsummu, mēs iegūtu vidējo ražību kā intensitātes relatīvo lielumu. Tas būtu
visprecīzākais rezultāts, jo absolūtos lielumus parasti pieraksta un publicē ar
lielāku zīmīgo ciparu skaitu, turklāt uzdevuma atrisinājumam jāizpilda vismazāk
darbību.
Redzam,
ka piemēru, kurš ilustrē svērtā aritmētiskā vidējā lietošanas trešo uzdevumu
grupu, var atrisināt precīzāk, reducējot to uz pirmo uzdevumu grupu, ja vien ir
pieejama vajadzīgā sākotnējā informācija. Tādēļ īsto un teorētiski
vispamatotāko svērtā aritmētiskā vidējā lietošanu raksturo pirmā uzdevuma
grupa.
Savukārt,
ja atrisinot izvirzīto uzdevumu, 1.1. tabulā nebūtu datu par sējumu platību pa
grupām (pēdējā aile), par statistiskajiem svariem vajadzētu ņemt saimniecību
skaitu pa grupām, kas samazinātu vidējā precizitāti.
Vispār,
rēķinot svērto aritmētisko vidējo pēc intervālu variācijas rindas, tuvinājums
ir pilnīgi pietiekams, ja intervāli ir pietiekami šauri un vienību skaits tajos
ir liels. Tuvinājums ir nepietiekams, ja kopa ir sagrupēta tikai divās vai trīs
grupās. Lielas kļūdas var rasties, ja grupējumā ir lietoti vaļējie intervāli,
kuros ir daudz vienību, bet apstrādes gaitā tie formāli tiek pārveidoti par
slēgtiem intervāliem, pieņemot, ka šie intervāli ir tikpat gari (lieli) kā
pārējie.
1.2.5. Aritmētiskā vidējā īpašības
Arimētiskajam vidējam ir
vairākas īpašības. Pirmās divas īpašības raksturo aritmētiskā vidējā būtību.
Pārējās īpašības ir saistītas ar formulu pārveidojumiem, kas var atvieglot
aritmētiskā vidējā aprēķinus.
1.Noviržu summa no aritmētiskā
vidējā ir nulle(nulles īpašība).
![]() , ja svari ir vienādi vai to nav,
, ja svari ir vienādi vai to nav,
![]() , ja svari dažādi. (1.6)
, ja svari dažādi. (1.6)
Pierādījums
nesvērtam vidējam. Izteiksmē (1.6) summē katru locekli atsevišķi, ![]() aizstāj ar tā
vērtību no formulas(1.4) un konstantā lieluma
aizstāj ar tā
vērtību no formulas(1.4) un konstantā lieluma ![]() summēšanas vietā liek
tā reizinājumu ar saskaitāmo skaitu n:
summēšanas vietā liek
tā reizinājumu ar saskaitāmo skaitu n: ![]() .
.
2. Noviržu kvadrātu summa no aritmētiskā vidējā
ir minimāla (vismazāko kvadrātu īpašība):
![]() , ja c
, ja c![]() .
.
Šo pašu īpašību var izteikt arī ar vienādību
nesvērtam
vidējam:
![]() ; (1.7)
; (1.7)
svērtam
vidējam:
![]() . (1.7a)
. (1.7a)
Pierādījums
nesvērtam vidējam.
No starpības x-c atņem un tai pieskaita konstantu lielumu
![]() , sagrupē saskaitāmos, binomu kāpina kvadrātā un konstantu
lielumu saskaitīšanu aizstāj ar reizināšanu:
, sagrupē saskaitāmos, binomu kāpina kvadrātā un konstantu
lielumu saskaitīšanu aizstāj ar reizināšanu:
![]()
![]()
![]()
Bet, tā
kā saskaņā ar aritmētiskā vidējā pirmo īpašību ![]() , tad otrais loceklis ir vienāds ar nulli un
, tad otrais loceklis ir vienāds ar nulli un ![]()
![]()
![]() , no kā izriet, ka
, no kā izriet, ka ![]()
Ir
izstrādāti daudzi paņēmieni aritmētiskā vidējā aprēķina vienkāršošanai,
ja ir jālieto rokas skaitļošanas mašīnas (kalkulatori). Agrāk matemātiskās
statistikas kursos tiem pievērsa lielu vērību. Tagad, kad praktisko skaitļošanu
veic ar datoriem, šos paņēmienus lieto reti un tie zaudē savu nozīmi. Tādēļ tos
aplūkosim bez pierādījumiem un piemēriem.
3. Ja
no visiem lielumiem x, kuru vidējo
aprēķina (x var būt nesagrupēti dati, varianti vai intervālu centri) atņem
vienu un to pašu konstantu lielumu c
un starpībām x-c aprēķina aritmētisko
vidējo, tad tas ir par to pašu konstanto lielumu c mazāks nekā sākotnējo datu aritmētiskais vidējais. Lai atrastu sākotnējo
lielumu aritmētisko vidējo, samazināto lielumu vidējam jāpieskaita konstante c.
4. Ja
visus nesagrupētus datus (variantus vai intervālu centrus) x samazina ![]() reizes (izdala ar
reizes (izdala ar ![]() ) un dalījumiem aprēķina aritmētisko vidējo, samazināto
lielumu vidējais ir jāreizina ar
) un dalījumiem aprēķina aritmētisko vidējo, samazināto
lielumu vidējais ir jāreizina ar ![]() .
.
5. Ja
visu datu (variantu) statistiskie svari ir vienādi, svērtais aritmētiskais
vidējais ir vienāds ar vienkāršo vidējo.
6. Ja
visu svaru sistēmu reizina vai dala ar vienu un to pašu skaitli, svērtais
aritmētiskais vidējais nemaimās. Ja svaru summa ir vienāda ar 1, aritmētisko
vidējo var aprēķināt pēc formulas ![]() , kur v - relatīvie biežumi. Tā kā
, kur v - relatīvie biežumi. Tā kā ![]() , dalīšanai ar svaru summu nav nozīmes. No tā secina, ka
aprēķinot svērto aritmētisko vidējo, absolūto biežumu vietā var lietot
relatīvos biežumus.
, dalīšanai ar svaru summu nav nozīmes. No tā secina, ka
aprēķinot svērto aritmētisko vidējo, absolūto biežumu vietā var lietot
relatīvos biežumus.
7.Ja
statistikā kopa ir sadalīta k grupās
un ir izrēķināti grupu aritmētiskie vidējie, tad visas kopas svērto aritmētisko
vidējo var aprēķināt kā grupu vidējo svērto aritmētisko vidējo:
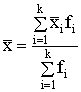 , (1.8)
, (1.8)
kur ![]() - i-tās grupas
svērtais aritmētiskais vidējais;
- i-tās grupas
svērtais aritmētiskais vidējais;
fi
- i-tās grupas statistiskais svars;
k
- grupu skaits.
Ja,
aprēķinot grupu vidējos, par statistiskajiem svariem pamatoti ir izmantots
kopas vienību skaits apakšgrupās, tad katras grupas statistiskais svars ir
vienāds ar kopas vienību skaitu grupā:fi=ni, turklāt ![]() .
.
1.2.6. Harmoniskais vidējais
Harmonisko vidējo iegūst, pakāpju vidējā formulā ņemot z=-1. Tā kā
x-1=![]() , tad
, tad
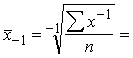
![]() . (1.9)
. (1.9)
Svērtā harmoniskā vidējā formula ir šāda:
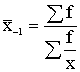 . (1.10)
. (1.10)
1.2.7. Harmoniskā vidējā lietošana
Ja ir jāaprēķina absolūto
lielumu vidējais, tad uzdevumos ar ekonomikas saturu praktiski vienmēr
jālieto vienkāršais aritmētiskais vidējais. Jautājums ir sarežģītāks, ja ir
jāaprēķina relatīvo lielumu vidējie, it īpaši intensitātes relatīvo
lielumu vidējais.
Intensitātes relatīvo lielumu
iegūst kā divu dažādu absolūto lielumu (pazīmju) attiecību (dalījumu). Mainot
vietām šīs attiecības skaitītāju un saucēju, iegūst tiešos un apgrieztos
intensitātes relatīvos lielumus.
Parādīsim, kā dažas ļoti
svarīgas ekonomikas kategorijas skaitliski raksturo ar tiešajiem un
apgrieztajiem intensitātes relatīvajiem lielumiem (skat. 1.3 tabulu).
1.3. tabula
Tiešie un apgrieztie intensitātes relatīvie lielumi, kas raksturo dažas
svarīgas ekonomikas kategorijas
|
Pētījamā
ekonomikas kategorija (parādība) |
Tiešais
lielums x |
Apgrieztais
lielums
|
|
1. Darba ražīgums |
Ražotā produkcija vienā laika vienībā (produkcijas
daudzuma rādītāju dala ar patērētā darba laika rādītāju) |
Darba patēriņš vienas produkcijas vienības ražošanai;
darbietilpība (patērētā darba laika rādītāju dala ar ražotās produkcijas
daudzuma rādītāju) |
|
2. Ražošanas fondu izmantošanas līmenis |
Ražotā produkcija uz vienu fondu vienību, parasti vērtības
izteiksmē (fondu atdeve, kapitāla atdeve) |
Ražošanas fondi (parasti vērtības izteiksmē) uz vienu
produkcijas vienību (fondu ietilpība, kapitālietilpība) |
|
3.Naudas pirktspēja |
Preces daudzums, ko var nopirkt par vienu naudas
vienību (latu) |
Preces vienas vienības cena |
|
4.Kapitāla (fondu) aprite |
Investīcijas apjoms laika vienībā |
Kapitāla (fondu) aprites laiks |
|
5.Transporta kustības ātrums |
Nobrauktais ceļa garums laika vienībā, piem. stundā |
Laika patēriņš noteikta attāluma (piem., 100km)
nobraukšanai |
No matemātikas
viedokļa tiešie un apgrieztie relatīvie lielumi ir savstarpēji apgriezti. Tādēļ
formāli jebkuru no tiem var pieņemt par tiešo. Vadoties no rādītāju satura,
ekonomikā par tiešajiem lielumiem sauc tos, kuri palielinās, no loģikas
viedokļa palielinoties pētījamai ekonomikas kategrijai. Piem., pieaugot darba
ražīgumam, palielinās ražotās produkcijas daudzums laika vienībā. Apgrieztie
lielumi tādos pat apstākļos samazinās. Piemēram, pieaugot darba ražīgumam,
samazinās darba patēriņš vienas produkcijas vienības ražošanai.
Viegli pārliecināties, ka tiešā
un apgrieztā individuālo intensitātes relatīvo lielumu reizinājums ir 1:
![]()
Tādēļ ir loģiski nepieciešams,
lai arī tiešo un apgriezto lielumu vidējie atbilstu šai sakarībai. Ir
jānodrošina, lai
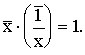 (1.11)
(1.11)
Izmantojot viegli pārskatāmu piemēru, parādīsim, kā to
panāk (skat.1.4.tabulu).
1.4. tabula
Trīs strādnieku darba ražīguma analīze
|
Strādnieka
tabelas Nr. |
Ražota
produkcija gab. |
Patērēts
darba laiks stundas f |
Darba
ražīgums stundā x |
Darba
patēriņš vienas vienības ražošanai
|
|
1. |
16 |
8 |
2 |
0,5 |
|
2. |
9 |
9 |
1 |
1,0 |
|
3. |
9 |
6 |
1,5 |
0,667 |
|
Kopā Vidēji |
34 ´ |
23 ´ |
´ 1,48 |
´ 0,676 |
Aprēķinām
tiešā un netiešā darba ražīguma rādītāju vidējos lielumus kā summāros
intensitātes relatīvos lielumus:
![]() (gabali stundā);
(gabali stundā);
![]()
![]() (stundas viena gabala ražošanai).
(stundas viena gabala ražošanai).
Sakarība 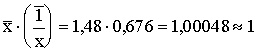 izpildās, ņemot vērā,
ka
izpildās, ņemot vērā,
ka ![]() un
un ![]() pierakstīti tuvināti.
pierakstīti tuvināti.
Pārbaudām, kā šos pašus
lielumus var iegūt, lietojot svērto vidējo formulas.
Vidējais darba ražīgums ir
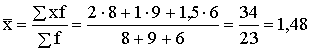 ,
,
kas sakrīt ar iepriekšējo.
Par
statistiskajiem svariem f izmantojām katra strādnieka patērēto (nostrādāto)
darba laiku. Tas ir lielums, kurš, veidojot darba ražīguma tiešo rādītāju,
atrodas attiecības saucējā.
Tādā pašā veidā rēķinot apgrieztā darba ražīguma rādītāja
vidējo, pareizu rezultātu neiegūstam:
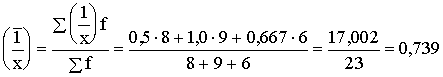 .
.
Pareizu apgriezto lielumu
vidējo var iegūt divejādi.
Pirmais paņēmiens saglabā
aritmētiskā vidējā formu, bet izmaina svaru sistēmu. Šajā gadījumā par svariem
jāņem ražotās produkcijas daudzums, t.i. lielums, kurš atrodas individuālo apgriezto
relatīvo lielumu saucējā, bet tiešo relatīvo lielumu skaitītājā.Šos
svarus bieži apzīmē ar M un var
aprēķināt arī šādi M=xf. Piemēram,
pirmajam strādniekam M=2×8=16(gab.).
Tādējādi
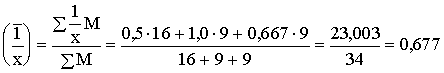 .
.
Ja grib paturēt sākotnējo svaru
sistēmu, tad apgriezto lielumu vidējais ir jārēķina kā harmoniskais vidējais
(otrais paņēmiens).
Aizstājot formulā(1.10) x ar ![]() (jo mēs rēķinām nevis parasto, bet apgriezto lielumu vidējo)
iegūst svērtā harmoniskā vidējā formulu, kādu parasti uzrāda statistikas
kursos:
(jo mēs rēķinām nevis parasto, bet apgriezto lielumu vidējo)
iegūst svērtā harmoniskā vidējā formulu, kādu parasti uzrāda statistikas
kursos:
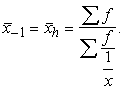 (1.12)
(1.12)
Lai
nerastos ilūzija, ka šī formula pēc būtības atšķiras no (1.10) var izdarīt
substitūciju ![]() (apgrieztos relatīvos
lielumus apzīmēt ar z), iegūstot formulu, kas precīzi sakrīt ar (1.10).
(apgrieztos relatīvos
lielumus apzīmēt ar z), iegūstot formulu, kas precīzi sakrīt ar (1.10).
Piemērā
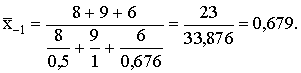
Esam
ieguvuši pareizo rezultātu, ja neņem vērā atšķirības pēdējā skaitļa šķirā
starprezultātu noapaļošanas dēļ.
Statistikas
praksē nav vienprātības par to, vai vidējos ![]() un
un 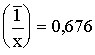 abus uzskatīt par
aritmētiskiem vidējiem, kas ir jāaprēķina, izmantojot dažādas svaru sistēmas,
vai attiecīgi par aritmētisko un harmonisko vidējo, kuri aprēķināti ar vienu un
to pašu svaru sistēmu f.
abus uzskatīt par
aritmētiskiem vidējiem, kas ir jāaprēķina, izmantojot dažādas svaru sistēmas,
vai attiecīgi par aritmētisko un harmonisko vidējo, kuri aprēķināti ar vienu un
to pašu svaru sistēmu f.
Pēc
mūsu domām pamatotāks ir otrais viedoklis, jo neprasa pamatot citu īpašu svaru
sistēmu un vairāk akcentē uzmanību uz vidējā lieluma būtību, bet mazāk - uz
izskaitļošanas tehniku. Pieņemot šo viedokli, var secināt, ka tiešo
relatīvo lielumu vidējais ir jārēķina kā svērtais aritmētiskais vidējais, bet
apgriezto relatīvo lielumu - kā svērtais harmoniskais vidējais.
Protams
apgriezto lielumu vidējo var izskaitļot arī kā aritmētisko vidējo, izmainot
sākotnējo svaru sistēmu M=xf, bet tas nemaina vidējā būtību. Tāpat ir iespējams
izskaitļot pēc dotajiem individuālajiem apgrieztajiem lielumiem ![]() sākotnēji nezināmos
tiešos lielumus x, aprēķināt ar parasto svaru sistēmu f viņu svērto aritmētisko
vidējo
sākotnēji nezināmos
tiešos lielumus x, aprēķināt ar parasto svaru sistēmu f viņu svērto aritmētisko
vidējo ![]() un visbeidzot
aprēķināt viņa apgriezto lielumu
un visbeidzot
aprēķināt viņa apgriezto lielumu ![]() . Arī šāds ceļš ved pie vēlamā mērķa - apgriezto lielumu
pareiza vidējā lieluma - un bieži ir ja ne īsāks, tad pārskatāmāks. Tomēr tas
nemaina vidējā
. Arī šāds ceļš ved pie vēlamā mērķa - apgriezto lielumu
pareiza vidējā lieluma - un bieži ir ja ne īsāks, tad pārskatāmāks. Tomēr tas
nemaina vidējā ![]() būtību, kurš pēc savām
īpašībām ir svērtais harmoniskais vidējais.
būtību, kurš pēc savām
īpašībām ir svērtais harmoniskais vidējais.
Dažādi
ceļi vidējo lielumu aprēķināšanā ir iespējami tad, ja vienas un tās pašas
kategorijas(parādības) skaitliskai raksturošanai ir definēti un tiek lietoti
gan tiešie gan apgrieztie lielumi. Ekonomikā visbiežāk tā arī ir. Turpretī
tehnikā nereti izmērī un lieto tikai vienu lielumu, piemēram, apgriezto.
Radioelektronikā,
lai raksturotu rezistorus un dažus citus elektriskās ķēdes elementus, izmanto
rādītāju “aktīvā pretestība” (omos, kiloomos, megaomos).Īstenībā tas ir
apgrieztais lielums īpašībai “vadītspēja”. Pēdējā ir definēta un to izsaka
“sīmensons’, taču praksē lieto reti. Tādēļ vajadzīgie aprēķini parasti ir
jāizdara ar apgriestajiem lielumiem. Piemēram, radioamatierim ielodēšanai
elektriskajā shēmā ir vajadzīga 500W aktīva pretestība. Tuvākā
nominālā rezistoru vērtība, ko ražo saskaņā ar standartu, ir 510W. Ja ir
vēlēšanās iegūt lielāku precizitāti, var saslēgt virknē divus zemomīgākus
rezistorus, piem., 270 un 330W. Ja to
pašu rezultātu grib sasniegt, saslēdzot paralēli divus vai vairākus augstomīgākus
rezistorus, jālieto formula
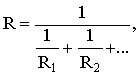
kur R - vajadzīgā, bet R1
un R2 paralēli saslēgto rezistoru pretestības. Manipulējot ar R1
un R2 (vajadzības gadījumā R3 utt.) vērtībām, var iegūt
vajadzīgo R.
Piem.,ja
R vajadzīgs 500W, bet R1
izvēlamies 750W, tad R2
jāņem 1500W.
Iepriekšējā
formula kļūst identiska ar harmoniskā vidējā formulu (1.10), ja tās abas puses
pareizina ar n, tad nR=![]() , piemērā tā ir harmoniskā vidējā divu izmantoto rezistoru (R1=750W un R2=1500W) pretestība
nR=2×500=1000W.
, piemērā tā ir harmoniskā vidējā divu izmantoto rezistoru (R1=750W un R2=1500W) pretestība
nR=2×500=1000W.
Izdarīt
analogus aprēķinus, izmantojot tiešos lielumus - rezistoru vadītspēju sīmensos
- būtu šķietami vieglāk, bet praktiski tas grūtāk, jo visu elektrisko shēmu
elementu aktīvās pretestības uzrāda omos, tāpat marķē rezistorus u.c.
elementus, graduē mērinstrumentu skalas.
Tāda
radioelektroniska lieluma kā kapacitāte apgrieztais lielums elementārajā
radiotehnikā vispār netiek definēts. Tādēļ vairāku virknē saslēgtu kondensātoru
kopējo kapacitāti vienmēr nākas aprēķināt ar formulu
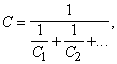
kur C1, C2, … - virknē saslēgto
kondensātoru kapacitātes, C - šīs ķēdes kopējā kapacitāte.
Pēdējās
formulas tieši izriet no harmoniskā vidējā formulas.
Ja
ekonomikā lietoto rādītāju un formulu izvēli nākas pamatot ar loģiskiem
profesionāliem apsvērumiem, kas vienmēr pieļauj tādu vai citādu diskusiju
iespēju, tad tehnikā (vismaz lielākajā daļā gadījumu) izdarīto aprēķinu un līdz
ar to lietoto formulu pareizību viegli pārbaudīt ar tiešiem mērijumiem,
izmantojot atbilstošos mērinstrumentus.
1.2.8.Ģeometriskais vidējais
Ģeometrisko vidējo iegūst
kā pakāpju vidējā robežu, ja ![]() .
.
Ir pierādīts, ka šī robeža ir
![]() (1.13)
(1.13)
Ģeometrisko vidējo izskaitļo,
lietojot logaritmus:
![]() (1.14)
(1.14)
Ja ir jāaprēķina svērtais
ģeometriskais vidējais, lieto formulu
![]()
kuru pārveido logaritmējot,
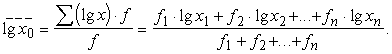 (1.15)
(1.15)
Ģeometriskā vidējā logaritms ir
vienāds ar datu variantu logaritmu arimētisko vidējo.
Ģeometrisko vidējo galvenokārt
lieto dinamikas rindu apstrādē. Ar to aprēķina vidējos augšanas
tempus2.
Piemērs. Aprēķināt ikmēneša ķēdes augšanas tempus un vidējo
augšanas tempu četros mēnešos, izmantojot 1.5. tabulas datus.
1.5.tabula
Rūpniecības uzņēmuma ražošanas apjoms
gada pirmajos četros mēnešos (tūkst.Ls)
|
|
Janvāris |
Februāris |
Marts |
Aprīlis |
|
Produkcijas apjoms |
10,2 |
11,1 |
11,3 |
12,0 |
Atrisinājums. Ķēdes augšanas tempi ir šādi: TII:I=![]() =1,088; TIII:II=
=1,088; TIII:II=![]() =1,018; TIV:III=
=1,018; TIV:III=![]() =1,062.
=1,062.
Vidējo augšanas tempu aprēķina
kā ģeometrisko vidējo:
![]()
___________________
2 Plašāk
skat. grāmatas nodaļu par dinamikas rindām.
1.2.9. Kvadrātiskais vidējais
Kvadrātisko vidējo iegūst,
pakāpju vidējā formulā ņemot z=2. Tad
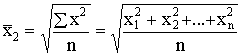 . (1.16)
. (1.16)
Svērto kvadrātisko vidējo
aprēķina pēc formulas
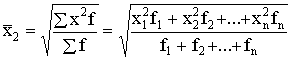 . (1.17)
. (1.17)
Kvadrātisko vidējo plašāk lieto
divos gadījumos.
Pirmais gadījums. Ir
jārēķina vidējais datiem, kuri ir izteikti novirzēs no kāda cita vidējā.
Piemēram, ir jāaprēķina detaļu svara vidējā novirze no normas. Šajā gadījumā
nevar rēķināt noviržu aritmētisko vidējo. Tas vislabāk saprotams tad, ja
noviržu no normas vietā ņem novirzes no aritmētiskā vidējā (vidējā svara). Tādu
noviržu algebriskā summa saskaņā ar aritmētiskā vidējā pirmo īpašību vienmēr ir
vienāda ar nulli. Tāpat arī noviržu no normas summa parasti ir tuva nullei.
Šādā gadījumā summējot novirzes, ir vai nu jāsummē noviržu absolūtās vērtības,
vai arī noviržu kvadrāti. Pēdējo summu dalot ar noviržu skaitu iegūstam
kvadrātisko vidējo.
Aprēķinot
vidējo kvadrātisko novirzi, mēs īstenībā raksturojam ne pazīmes centrālo
tendenci, bet pazīmes variāciju. Tādēļ vidējā kvadrātiskā novirze
(standartnovirze) plašāk tiks aplūkota apakšnodaļā “Variācijas rādītāji”.
Otrais gadījums. Ir jāaprēķina kādu
lineāru mērījumu (kvadrātu malu, apļu diametru u.t.t.) vidējais lielums,
turklāt zinātniski praktiska interese ir ne tikdaudz par pašiem šiem
mērijumiem, bet par figūru laukumiem, ko šie mērījumi raksturo.
Aprēķinot,
piemēram, vidējo kvadrātisko apļu diametru, ar tā palīdzību var konstruēt apli,
kura laukums atbilst sākotnējo apļu laukumu aritmētiskai vidējai vērtībai. Ejot
šādu ceļu, dažreiz vieglāk aprēķināt visu novēroto figūru (apļu) kopējo
laukumu. Netiešā veidā šo paņēmienu lieto mežu taksācijā, novērtējot koksnes
krājumu kādā platībā pēc atsevišķu koku diametra (krūšu augstumā) mērījumiem.
Vēl jāņem vērā koku garums.
1.2.10. Pakāpju vidējo mažoritāte
Katram
statistikas uzdevumam, kurā jāaprēķina vidējais lielums, vispiemērotākais ir
viens noteikts vidējais, kurš vislabāk atspoguļo pētāmo objektu vai parādību.
Tomēr formāli katrā uzdevumā var aprēķināt visus vidējā lieluma veidus. Līdz ar
to var rasties jatājums kā, lietojot dažādus vidējā lieluma veidus, atšķirsies
iegūtie rezultāti.
Ja pēc
vienas un tās pašas informācijas, izmantojot vienus un tos pašus statistiskos
svarus, aprēķina vairākus pakāpju vidējos, tad lielāks ir tas vidējais, kura
formulā ir lielāks pakāpes rādītājs z. Šo likumu sauc par pakāpju vidējo mažoritātes
likumu un pierāda vispārīgā veidā. Saskaņā ar mažoritātes likumu
![]() , (1.18)
, (1.18)
kur x-1
- harmoniskais vidējais (z=-1); x0 - ģeometriskais vidējais (z=0); ![]() - aritmētiskais
vidējais (z=1);
- aritmētiskais
vidējais (z=1); ![]() - kvadrātiskais
vidējais (z=2).
- kvadrātiskais
vidējais (z=2).
Mažoritātes
likums nav spēkā vienīgi triviālajā gadījumā, ja vidējie tiek aprēķināti
konstantu lielumu virknei. Dažādi vidējie vairāk atšķiras tad, ja datu
variācija ir lielāka.
1.2.11. Mediāna un kvartiles
Pazīstamākie
struktūras
vidējie ir mediāna un moda. Par mediānu sauc augošā vai dilstošā
kārtībā sakārtotas variācijas rindas vidū esošu variantu.
Ja
vienību skaits variācijas rindā ir nepāra skaitlis 2m+1, tad sakārtotas rindas
mediāna ir xm+1. Ja vienību skaits ir pāra skaitlis 2m, tad mediāna
ir variantu xm un xm+1 aritmētiskais vidējais. Apzīmējot
mediānu ar simbolu Me, to pašu var parādīt formulās
Me=xm+1,
ja n=2m+1; (1.19)
Me=![]() , ja n=2m. (1.20)
, ja n=2m. (1.20)
Lai
atrastu mediānu intervālu variācijas rindai, vispirms ir jāatrod mediānas
jeb
mediālais intervāls. To atrod, izmantojot kumulatīvo variācijas rindu.
Mediānas intervāls ir tas, kurā uzkrātie absolūtie biežumi pirmo reizi
pārsniedz pusi no kopas vienību skaita vai kurā uzkrātie relatīvie biežumi
pirmo reizi pārsniedz 50%. Tālāk pieņem, ka mediānas intervāla ietvaros
varianti sadalās vienmērīgi. Tas dod pamatu izmantot interpolācijas formulu.
Me=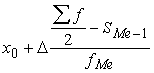 , (1.21)
, (1.21)
kur x0 - mediānas intervāla apakšējā robeža;
![]() - mediānas intervāla
garums;
- mediānas intervāla
garums;
SMe-1 - uzkrātais biežums intevālā, kas
atrodas pirms mediānas intervāla;
fMe - mediānas intervāla biežums;
![]() - kopējais novērojumu
skaits variācijas rindā.
- kopējais novērojumu
skaits variācijas rindā.
Piemērs. Aprēķināt mediānu 1.1. tabulā dotajai variācijas rindai.
Mediānas
intervālu var noteikt tieši no tabulas. Tas ir intervāls
18,01…22,0 cnt/ha, jo tajā uzkrātais relatīvais biežums3 pirmo reizi pārsniedz 50% (piemērā tieši 50%). Pēc
tabulas datiem nosaka mediānas aprēķināšanas formulā
vajadzīgos lielumus:
x0=18;
![]() =4; SMe-1=20; fMe=30;
=4; SMe-1=20; fMe=30; ![]() =50.
=50.
Tālāk var lietot formulu
(1.21).
Me=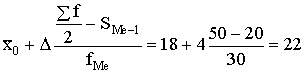 (cnt/ha).
(cnt/ha).
________________________
3 Rēķinot mediānu, modu u.c. rādītājus, parasti
interesējas tieši par kopas vienību (saimniecību) sadalījumu, tādēļ attiecīgos
biežumus arī izmanto aprēķinos. Tomēr var būt gadījumi, kad ir lietderīgi
izmantot tos statistiskos svarus, kurus lietojām svērtā aritmētiskā vidējā
aprēķināšanā (sējumu platību sadalījumu). Tad mediāna raksturos ražību, kura
visu sējumu platību dala divās vienādās daļās, un tā būs labāk salīdzināma ar
svērto aritmētisko vidējo.
Mediāna
ir 22cnt/ha. Tā sakrīt ar mediānas intervāla augšējo robežu, jo uzkrātais biežums
šajā intevālā sasniedz tieši 50%. Ja tas 50% pārsniegtu, mediāna atrastos
mediānas intervāla robežās. Ja saimniecību sadalījums mediānas intervāla
robežās ir vienmērīgs4 ,
tad pusē no visas kopas saimniecībām graudaugu ražība ir bijusi mazāka par
22cnt/ha, bet pusē - lielāka. Šīs pašas kopas graudaugu ražības aritmētiskais
vidējais bija 22,5cnt/ha. Tā tas ir vienmēr, kad sadalījums nav simetrisks. Ja
sadalījums ir pilnīgi simetrisks, mediāna un aritmētiskais vidējais ir vienādi.
Izmantojot šo īpašību, var izveidot samērā vienkāršus sadalījuma asimetrijas
rādītājus.
Analogi
mediānai aprēķina arī virkni citu variācijas rindas struktūras rādītāju. Šie
rādītāji gan nav pieskaitāmi vidējiem lielumiem, tomēr, ņemot vērā viņu
lietderību, izdarot samērā vienkāršu sadalījuma analīzi, dažus no tiem
aplūkosim.
Plaši
lieto sadalījuma kvartiles. Tās ir pētītās pazīmes vērtības, kas sakārtotu
variācijas rindu dala četrās līdzīgās daļās tā, ka katrā no tām nonāk 25% kopas
vienību. Ir trīs kvartiles: pirmā Q1, otrā Q2 un trešā Q3.
Pirmā kvartile ir pazīmes vērtība par kuru sakārtotā rindā 25% kopas vienībām
ir reģistrētas mazākas vērtības. Otrā kvartile tādā pat veidā nodala 50% kopas
vienību, tātad ir vienāda ar mediānu, bet trešā 75% kopas vienību.
Ja mediāna jau ir aprēķināta,
otrā kvartile vairs nav jāaprēķina. Lai aprēķinātu pirmo un trešo kvartili,
grupētu datus gadījumā vispirms nosaka šīs kvartiles saturošos intervālus. Tie
ir intervāli, kur sakārtotu uzkrāto biežumu rindā biežumi pirmo reizi pārsteidz
attiecīgi 25% un 75% no kopas vienību skaita.
Pašas kvartiles atrod ar
interpolācijas formulām, kas ir analogas mediānas formulai.
Q1=x1+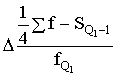 , (1.22)
, (1.22)
Q3=x3+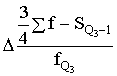 , (1.23)
, (1.23)
kur
Q1 un Q3
- pirmā un trešā kvartile,
x1 un x3
- pirmo un trešo kvartili saturošo intervālu apakšējās robežas,
![]() - kvartili saturošā
intervāla garums. Formulas lietošana pamatotāka, ja visi intervāli ir vienāda
garuma, vismaz kvartili saturošais un iepriekšējais intervāli,
- kvartili saturošā
intervāla garums. Formulas lietošana pamatotāka, ja visi intervāli ir vienāda
garuma, vismaz kvartili saturošais un iepriekšējais intervāli,
![]() un
un ![]() - tā intevāla, kurš
atrodas pirms attiecīgā kvartili saturošā intervāla, uzkrātais biežums,
- tā intevāla, kurš
atrodas pirms attiecīgā kvartili saturošā intervāla, uzkrātais biežums,
![]() un
un ![]() - attiecīgo kvartili
saturošā intervāla tiešais (neuzkrātais) biežums,
- attiecīgo kvartili
saturošā intervāla tiešais (neuzkrātais) biežums,
![]() - kopas vienību
skaits.
- kopas vienību
skaits.
Variācijas rindas otrā kvartile
ir mediāna Q2=Me.
________________________
4 Šī atruna,
kas ir vajadzīga vispārējam gadījumam, nav vajadzīga piemēram, jo mediāna
sakrīt ar intervāla robežu.
Aprēķināsim
pirmo un trešo kvartili lauksaimniecības uzņēmumu sadalījumam pēc 1.1.tabulas
datiem, izmantojot saimniecību skaita uzkrātos relatīvos biežumus. Pēc 7.ailes
datiem ir redzams, ka 1.kvartile atrodas 3.intervālā (turpat kur mediāna), jo
uzkrātais relatīvais biežums 50% pirmo reizi pārsniedz 25%. Trešā kvartile
atrodas 4.intervālā, jo uzkrātais relatīvais biežums 78% pirmo reizi pārsniedz
75%. Līdz ar to no 1.1 tabulas var nolasīt formulās ievietojamos lielumus :
x1=18; x3=22;
![]() =4;
=4; ![]() =20;
=20; ![]() =50;
=50;
![]() =30;
=30; ![]() =28;
=28; ![]() =100.
=100.
Izdarot attiecīgos
ievietojumus, iegūstam, ka
Q1=18+4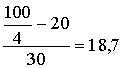 (cnt/ha);
(cnt/ha);
Q3=22+4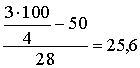 (cnt/ha).
(cnt/ha).
Atrastos
lielumus interpretē tā, ka dotajā ekoloģiskajā grupā ir 25% saimniecību, kur
graudaugu ražība bija mazāka par 18,7cnt/ha, un 25% saimniecību, kur ražība
bija virs 25,6cnt/ha. Atceramies, ka mediāna, kas dala sadalījumu uz pusēm,
bija 22cnt/ha.
Sakārtotu
variācijas rindu desmit vienādās daļās dala deciles, kuras aprēķina
līdzīgi kvartilēm.
Variācijas
rindu piecās līdzīgās daļās dala kvintiles, bet 100 vienādās daļās -
procentiles. Kvartiles, kvintiles, deciles u.c. šādus rādītājus apzīmē ar
kopēju terminu - kvantiles.
Pēdējā
laikā statistikas praksē ļoti plaši lieto deciļu grupējumus.
Piemēram
dzīves līmeņa statistikā visas pēc ienākuma uz vienu mājsaimniecības locekli
augošā secībā sakārtotas mājsaimniecības sadala desmit vienādās daļās.
Tālāk
var sīkāk izpētīt, piemēram, pirmo deciles grupu, t.i. 10% vistrūcīgāko
mājsaimniecību, aprēķinot dažādus citus rādītājus par šo grupu (vidējo
mājsaimniecību locekļu skaitu, izdevumus pārtikas iegādei u.t.t.). Līdzīgu
raksturojumu var izstrādāt par visām citām sabiedrības desmitdaļām.
Kvantiles
un vispār kopas vienību sakārtošanu (ranžēšanu) plaši izmanto neparametriskā
statistikā (skat. grāmatas pēdējo nodaļu).
1.2.12. Moda
Par modu
Mo sauc variantu, kurš sadalījuma rindā ir sastopams visbiežāk. Diskrētā vai
atributīvā variācijas rindā moda nolasāma tieši kā variants ar vislielāko
absolūto vai relatīvo biežumu.
Intervālu
rindā vispirms jānosaka modas jeb modālais intervāls. Tas
ir intervāls ar vislielāko biežumu.
Iepriekšējā
piemērā modālais intervāls ir no 18 līdz 22cnt/ha, jo šajā intevālā ir 30%
saimniecību - vairāk kā jebkurā citā intervālā. Konkrētajā piemērā modālais
intervāls sakrīt ar mediānas intervālu. Citos gadījumos tas tā var nebūt.
Intervālu
variācijas rindai modu aprēķina pēc interpolācijas formulas (1.24)(tās
pamatā ir hipotēze, ka sadalījums intervālu ietvaros ir vienmērīgs):
Mo=x0+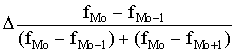 , (1.24)
, (1.24)
kur Mo - moda;
x0
- modālā intervāla apakšējā robeža;
![]() - modālā intervāla
garums;
- modālā intervāla
garums;
fMo
- modālā intervāla biežums;
fMo-1
- pirmsnodālā intervāla biežums;
fMo+1
- pēcmodālā intervāla biežums.
Aprēķināsim
modu 1.1.tabulā dotajai variācijas rindai. No tabulas atrodam, ka x0=18;
![]() =4; fMo=30; fMo-1=17; fMo+1=28.
Tad pēc formulas (1.24.)
=4; fMo=30; fMo-1=17; fMo+1=28.
Tad pēc formulas (1.24.)
Mo=x0+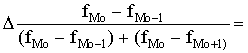
=18+4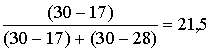 (cnt/ha).
(cnt/ha).
Graudaugu
ražības modālais lielums jeb visbiežāk sastopamā ražība šīs kopas saimniecībās
ir 21,5cnt/ha. Piemērā mediānas intervāls sakrīt ar modālo intervālu, taču
pašas mediāna un moda ir atšķirīgas.
Nosakot
mediānu, ņem vērā visus rindas locekļus, bet modu nosaka galvenokārt modālais
intervāls; interpolācijas gadījumā bez tam ņem vērā vēl pirmsmodālo un
pēcmodālo intervālus. Par sadalījuma raksturu pārējās variācijas rindas daļās,
aprēķinot modu, neinteresējas.
Modu
lieto galvenokārt tad, ja ir svarīgi izdalīt tieši to variantu, kurš sastopams
visbiežāk. Sevišķi raksturīgi tas ir diskrēta sadalījuma gadījumā. Tā,
piemēram, preču pieprasījuma statistikā moda var būt visbiežāk pieprasītais
apavu numurs, gatavo apģērbu numurs utt. Rēķināt šajā gadījumā aritmētisko
vidējo ir maznozīmīgi, jo nav vajadzīgs un nav paredzēts ražot, piemēram,
apavus, kuru izmērs tieši atbilstu aritmētiskajam vidējam (izmēru numurs ar
desmitdaļām un simtdaļām). Tāpat moda ir svarīgs atributīvas sadalījuma rindas
raksturotājs, jo aritmētisko vidējo lielumu un mediānu šādām rindām nevar
aprēķināt. Piemēram, var noteikt modālo (visizplatītāko) tautību, bet nevar
izrēķināt vidējo tautību.
Var
salīdzināt, kurš centrālās tendences rādītājs - aritmētiskais vidējais,
mediāna, moda - ir vairāk un kurš mazāk informatīvs. Aprēķinot aritmētisko
vidējo nesagrupētu skaitļu rindai, aprēķinos ņem vērā katra skaitļa tiešo vērtību
(lielumu). Tādēļ aritmētiskais vidējais ir maksimāli informatīvs centrālās
tendences rādītājs. Aprēķinot mediānu, ņem vērā tikai katra skaitļa vietu
ranžētā rindā, bet ne tā tiešo vērtību. Tādēļ daļa derīgās informācijas tiek
zaudēta, un mediāna ir mazāk informatīvs centrālās tendeces rādītājs nekā
aritmētiskais vidējais. Modu nosaka tikai modālais variants, bet intervālu
variācijas rindas gadījumā - modālais (daļēji pirms un pēcmodālais) intervāli.
Visa informācija, ko satur pārējie intervāli netiek izmantota. Tādēļ moda ir
vismazāk informatīvs centrālās tendences rādītājs.
1.3. Variācijas rādītāji un to īpašības
1.3.1. Variācijas rādītāji
Visvienkāršākais
variācijas rādītājs ir variācijas amplitūda jeb variācijas apjoms. Par variācijas
amplitūdu sauc starpību starp pazīmes lielāko un mazāko novēroto
skaitlisko vērtību. Apzīmējot šo rādītāju ar Rv, var rakstīt, ka
Rv=xmax-xmin, (1.25)
kur xmax
- pazīmes lielākā, bet xmin - mazākā vērtība.
Diskrētā
variācijas rindā variācijas amplitūdu var noteikt tieši un precīzi. Ja ir dota
intervālu rinda, variācijas amplitūdu var noteikt tikai aptuveni. Ja par
pazīmes mazāko vērtību ņem pirmā intervāla apakšējo robežu, bet par lielāko
vērtību - pēdējā intervāla augšējo robežu, tad variācijas amplitūda ir nedaudz
palielināta. Ja par šīm robežām ņem atbilstošo intervālu centrus, variācijas
amplitūda parasti ir nedaudz samazināta.
Iepriekš
(1.1. tabulā) apskatītajam saimniecību sadalījumam pēc graudaugu ražības
variācijas amlitūda pēc pirmās metodes ir Rv=34-10=24(cnt/ha), pēc otrās
metodes 32-12=20(cnt/ha).
Īsto
variācijas amplitūdu var konstatēt, izskatot sākotnējos, nesagrupētos datus.
Darba
algas variācijas amplitūda 1.2.3.paragrāfā apskatītajā piemērā par 8 strādnieku
brigādi ir Rv=250,31-190,15=60,16(lati).
Variācijas
amplitūda ir diezgan nedrošs variācijas rādītājs, jo tā ir atkarīga tikai no
galējiem variantiem. Nesagrupētu datu gadījumā - no divām viskrasāk
atšķirīgajām kopas vienībām. Statistikas praksē diezgan grūti nodrošināt
pilnīgu kopas viendabīgumu, tāpēc ir diezgan liela iespēja, ka samērā
viendabīgā kopā iekļūst viena vai vairākas krasi atšķirīgas vienības. Tādā
gadījumā variācijas amplitūda būs ievērojami palielināta.
Vidējo
absolūto jeb vidējo lineāro novirzi definē kā aritmētisko vidējo no
atsevišķu novērojumu (variantu) absolūtajām novirzēm no aritmētiskā vidējā. Ja
apstrādā nesagrupētus absolūtos lielumus, kā arī tad, ja variantu statistiskie
svari ir vienādi, lieto formulu
![]() , (1.26)
, (1.26)
kur ![]() - vidējā lineārā
novirze; n - kopas vienību skaits.
- vidējā lineārā
novirze; n - kopas vienību skaits.
Ja
atsevišķu novērojumu svari ir dažādi kā arī tad, ja ir jāapstrādā grupēti dati,
jālieto svērtā vidējā lineārā novirze:
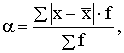 (1.27)
(1.27)
kur f -
statistiskie svari.
Tā kā
formulās (1.26) un (1.27) tiek summētas nevis novirzes, bet to moduļi, tad
vidējās lineārās novirzes īpašības ir sarežģītas.
Tādēļ
šo variācijas rādītāju statistikas praksē lieto reti. Tā lietošana ir pamatota
tad, ja aritmētiskā vidējā ![]() vietā izmanto mediānu
Me. Mediāna un vidējā lineārā novirze ir savstarpēji saistīti rādītāji. Par to
liecina viena no svarīgākajām mediānas īpašībām: summa, kuru iegūst saskaitot
novērojumu absolūtās novirzes no mediānas, ir mazāka nekā summa, kuru iegūst,
saskaitot novērojuma absolūtās novirzes no jebkura cita lieluma, kas nav
vienāds ar mediānu, t.i.,
vietā izmanto mediānu
Me. Mediāna un vidējā lineārā novirze ir savstarpēji saistīti rādītāji. Par to
liecina viena no svarīgākajām mediānas īpašībām: summa, kuru iegūst saskaitot
novērojumu absolūtās novirzes no mediānas, ir mazāka nekā summa, kuru iegūst,
saskaitot novērojuma absolūtās novirzes no jebkura cita lieluma, kas nav
vienāds ar mediānu, t.i.,
![]() , ja c
, ja c![]() Me. (1.28)
Me. (1.28)
Dispersija ir
statistikā visvairāk lietotais variācijas rādītājs. To apzīmē ar s2
vai ![]() . Apzīmējumu s2 lieto, ja dispersiju aprēķina pēc
izlases datiem, kura ņemta no kādas plašākas ģenerālkopas, un izlase to
reprezentē. Ģenerālkopas dispersiju un dispersiju teorētiskos pētījumos apzīmē
ar
. Apzīmējumu s2 lieto, ja dispersiju aprēķina pēc
izlases datiem, kura ņemta no kādas plašākas ģenerālkopas, un izlase to
reprezentē. Ģenerālkopas dispersiju un dispersiju teorētiskos pētījumos apzīmē
ar ![]() . Plašāk šie jautājumi aplūkoti nodaļā “Izlases metode”.
. Plašāk šie jautājumi aplūkoti nodaļā “Izlases metode”.
Ja
novērojumu statistiskie svari ir vienādi vai arī tos var neņemt vērā,
dispersiju aprēķina pēc formulas
s2=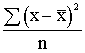 . (1.29)
. (1.29)
Ja statistiskie svari jāievēro,
lieto svērtās dispersijas formulu
s2=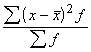 . (1.30)
. (1.30)
Statistiskie
svari jāievēro vienmēr, ja ir jāapstrādā iepriekš sagrupēti dati, tā kā par x
jāņem nevis atsevišķs novērojums, bet varianti.
Samērā
bieži kā starprezultātu fiksē noviržu kvadrātu summu, kas ir dispersijas
formulas skaitītājs. To apzīmē ar Q:
Q=![]() vai Q=
vai Q=![]() .
.
Aprēķināsim dispersiju,
izmantojot dažu iepriekšējā apakšnodaļā doto piemēru datus.
1.
Strādnieku algas dispersiju 8 cilvēku brigādē (sk. 1.2.3.§)
aprēķina pēc formulas 1.29., iepriekš izrēķinot, ka aritmētiskais vidējais ir
216,91 lati. Aprēķinus izdevīgi sakārtot tabulā.
1.6.tabula
Darba tabula dispersijas aprēķināšanai
|
Novērojumi
x |
215,27 |
230,91 |
190,15 |
250,31 |
201,50 |
222,93 |
219,10 |
205,12 |
|
|
Novirzes |
-1,64 |
14,00 |
-26,76 |
33,40 |
-15,41 |
6,02 |
2,19 |
-11,79 |
~0 |
|
Noviržu
kvadrāti |
2,690 |
196,000 |
716,098 |
1115,560 |
237,468 |
36,240 |
4,796 |
139,004 |
2447,856 |
s2=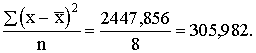
Dispersijas
vienība formāli ir sākotnējās datu vienības kvadrāts, piemērā iznāk lati
kvadrātā, kam nav reāla ekonomiska satura. Tādēļ dispersija ir svarīgs
starprezultāts citu ekonomiski interpretējamu variācijas rādītāju
aprēķināšanai, kā arī variācijas pakāpes salīdzinošai novērtēšanai dažādās
kopās vai vienas kopas daļās. Tiešus ekonomiskus secinājumus pēc dispersijas
neizdara. Tos izdara, aprēķinot standartnovirzi un variācijas koeficientu, kuri
aplūkoti šī paragrāfa beigu daļā.
Tāpat
profesionālas interpretācijas nav noviržu kvadrātu summai. Arī tās formālā
vienība ir sākotnējās vienības kvadrāts. Tās vienīgā nozīme varētu būt
uzmanības pievēršana, mainot sākotnējo vienību. Ja latu vietā gribam izmantot
tūkstošus latu, tad tiklab absolūtie, kā vidējie lielumi jādala ar 1000, bet
dispersija un noviržu kvadrātu summa ar 10002=1000000.
2.
Aprēķināsim atzīmju dispersiju 10 studentu grupai, sākotnējie dati par kuru
bija doti nodaļas sākumā (1.1.1§), bet
vidējās atzīmes aprēķins 1.2.3§ 2.
piemērā.
Tā kā
šajā gadījumā variantu nav daudz, ir izdevīgi saskaitīt to atkārtošanās reižu
skaitu un lietot formulu (1.30). Tā kā aprēķini ir nelieli, tos var izpildīt,
ievietojot datus tieši formulā, neizvēršot darba tabulā.
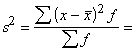
![]()
![]() .
.
![]()
3. Aprēķināsim graudaugu
ražības dispersiju, izmantojot 1.1.tabulas datus par statistiskajiem svariem
izmantojot sējumu platību īpatsvarus procentos. Strādājot ar neprogrammējamu
skaitļošanas mašīnu, darbu ērti izpildīt tabulā skat.1.7.tabulu. Tajā
vienlaikus ir izskaitļota arī summa ![]() , kas nepieciešama svērtā aritmētiskā vidējā aprēķināšanai.
, kas nepieciešama svērtā aritmētiskā vidējā aprēķināšanai.
1.7.tabula
Darba tabula svērtā aritmētiskā vidējā un svērtās dispersijas aprēķināšanai
graudaugu ražībai pirmās ekoloģiskās grupas saimniecībām pēc 1.1 tabulas datiem
|
Ražības
varianti x |
Sējumu
platība, procentos f |
xf |
x- |
(x- |
(x- |
|
12 16 20 24 28 32 |
2 16 30 28 18 6 |
24 256 600 672 504 192 |
-10,48 -6,48 -2,48 1,52 5,52 9,52 |
109,8304 41,9904 6,1504 2,3104 30,4704 90,6304 |
219,6608 671,8464 184,5120 64,6912 548,4672 543,7824 |
|
Kopā |
100 |
2248 |
5 |
5 |
2232,9600 |
Izmantojot 1.7.tabulā iegūtās
summas, aprēķinam:
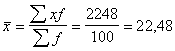 (cnt/ha);
(cnt/ha);
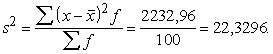
Analogi
aprēķini par otro ekoloģisko grupu (skat.1.2.tabulu), dod s2=22,5584.
Lai
iegūtu ekonomiski labi interpretējamu variācijas rādītāju, lieto standartnovirzi
jeb
vidējo kvadrātisko novirzi. Standartnovirzi definē kā
kvadrātsakni no dispersijas un apzīmē ar s vai s:
s=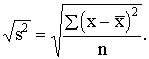 (1.31)
(1.31)
Izmantojot statistiskos svarus,
s=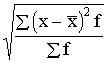 . (1.32)
. (1.32)
Graudaugu ražības
standartnovirzes iepriekš apskatītajā piemērā ir šādas:
pirmajā grupā s1=![]() =4,7254(cnt/ha);
=4,7254(cnt/ha);
otrajā grupā s2=![]() =4,7496(cnt/ha).
=4,7496(cnt/ha).
Standarnovirze,
tāpat kā aritmētiskais vidējais, ir izteikta variējošās pazīmes vienībās, piemērā - centneros no ha. Tādēļ šos
rādītājus parasti uzrāda kopā.
Graudaugu
vidējā ražība pirmās ekoloģiskās grupas saimniecībās ir 22,48 cnt/ha ar
standarnovirzi 4,73 cnt/ha, bet otrās - 20,04 cnt/ha ar standartnovirzi 4,75
cnt/ha. Ražības absolūtā variācija abās ekoloģiskajās grupās ir praktiski
vienāda.
Standartnovirzes
saturu vislabāk saprast, izveidojot centrētu, divkāršotu variācijas standartintervālu.
Tā apakšējo robežu atrod, atskaitot no aritmētiskā vidējā standartnovirzi, bet
augšējo - pieskaitot aritmētiskajam vidējam standartnovirzi. Piemērā par pirmo
ekoloģisko grupu divkāršota centrēta ražības variācijas standartintervāla
apakšējā robeža ir 22,48-4,73=17,75, bet augšējā robeža 22,48+4,73=27,21
(cnt/ha). Ja sējumu platību sadalījums pēc graudaugu ražības ir normāls, šajā
intervālā teorētiski ietilpst 68% sējumu platību. 1.1.tabulā uzrādīto intervālu
robežas nesakrīt ar tikko aprēķinātā variācijas standartintervāla robežām.
Izdarot tuvinātu intervālu sadalīšanu, pēc 1.1.tabulas iznāk, ka variācijas
standartintervālā nonāk aptuveni 68% no sējumu platības. Tātad faktiskais
sējumu platību sadalījums tā centālajā daļā labi atbilst normālajam
sadalījumam. Plašāk šie jautājumi aplūkoti apakšnodaļās “Normālais sadalījums”,
“Normālā sadalījuma aprēķināšana” u.c.
Aritmētiskais
vidējais un standartnovirze dod skaidri interpretējamus rādītājus gan par
pazīmes vidējo lielumu, gan par tās absolūto variāciju. Tomēr divu vai
vairāku variācijas rindu standartnovirzes savā starpā ir salīdzināmas vienīgi
tad, ja abu rindu vienības ir vienādas. Tad tās parāda, kurā rindā ir lielāka
absolūtā variācija. Ja salīdzināmo rindu vienības ir dažādas, standartnovirzes
nav salīdzināmas.
Ja
pētījumā izšķiroša nozīme ir nevis absolūtās, bet relatīvās variācijas
novērtēšanai, tad jāizmanto relatīvās variācijas rādītājs, kurš
ir nenosaukts skaitlis un nav atkarīgs ne no pētāmās pazīmes vienības, ne no
tās vidējā lieluma.
Variācijas
relatīvo lielumu raksturo variācijas koeficients, ko aprēķina,
dalot standartnovirzi ar aritmētisko vidējo:
![]() .
.
Šāds variācijas koeficients ir izteikts viena daļās. Ja
to vēlas izteikt procentos, tad iepriekšējais koeficients jāpareizina ar 100
vai jālieto formula
![]() . (1.33)
. (1.33)
Turpinot
iepriekšējo piemēru, var izrēķināt graudaugu ražības variācijas koeficientus
abām ekoloģiskajām grupām.
Pirmai: 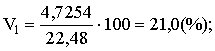
otrai: 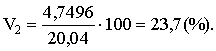
Tātad
graudaugu ražības relatīvā variācija otrā ekoloģiskajā grupā ir lielāka, kaut
gan absolūtās variācijas mēri gandrīz sakrīt. Cēlonis ir zemāka vidējā ražība
otrās grupas saimniecībās.
Katram
variācijas rādītājam ir savs spacifisks statistisks saturs. Praktiskajam darbam
ir jāizvēlas tas rādītājs, kurš ir visvairāk piemērots konkrētu analīzes mērķu
sasniegšanai.
1.3.2. Dispersijas īpašības
Dispersijas īpašības var pierādīt, algebriski pārveidojot
pamatformulas. Īpašības izmanto aprēķinu vienkāršošanai un labākai izpratnei.
1. Konstanta
lieluma dispersija ir vienāda ar nulli. Ja visi novērojumi ir vienādi, tad nav
variācijas un visi variācijas rādītāji ir vienādi ar nulli.
2. Ja no
visiem novērojumiem atņem kādu konstantu lielumu, tad dispersija nemainās. Šo
īpašību izmanto tad, ja visi novērojumi ir lieli skaitļi, kuri savā starpā
atšķiras maz.
3. Ja
visus novērojumus reizina (dala) ar konstantu lielumu ![]() , tad dispersija pieaug (samazinās)
, tad dispersija pieaug (samazinās) ![]() reizes. Šo īpašību var
izmantot, aprēķinot dispersiju pēc intervālu variācijas rindas. Pēc dalot
samazinātiem variantiem aprēķināto dispersiju (starprezultātu), aprēķinus
nobeidzot, pareizina ar
reizes. Šo īpašību var
izmantot, aprēķinot dispersiju pēc intervālu variācijas rindas. Pēc dalot
samazinātiem variantiem aprēķināto dispersiju (starprezultātu), aprēķinus
nobeidzot, pareizina ar ![]() .
.
4. Ja,
aprēķinot dispersiju, aritmētiko vidējo aizstāj ar kādu citu konstantu lielumu
c, tad dispersija pieaug par lielumu ![]() . No tā izriet, ka dispersiju var aprēķināt pēc formulas
. No tā izriet, ka dispersiju var aprēķināt pēc formulas
s2=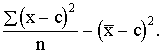 (1.34)
(1.34)
Ja par konstanto lielumu ņem
nulli, t.i., c=0, tad iegūst formulu
s2=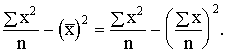 (1.35)
(1.35)
Ja izmanto statistiskos svarus,
analoga formula ir šāda:
s2=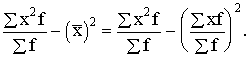 (1.36)
(1.36)
Pēdējās
divas formulas parasti lieto, aprēķinot dispersijas ar taustiņu skaitļošanas
mašīnām. Salīdzinājumā ar pamatformulām tām ir lielas priekšrocības, aprēķinot
dispersijas arī ar datortehniku. Lai aprēķinātu dispersiju pēc pamatformulām
(1.29) un (1.30), vispirms jāaprēķina aritmētiskais vidējais. Lai to izdarītu,
ir jāapstrādā visi sākotnējie dati, atrodot ![]() vai
vai ![]() . Ja sākotnējo datu ir daudz, tie jāievada mašīnas
operatīvajā atmiņā pa daļām. Tālāk, lai aprēķinātu noviržu kvadrātu summas
. Ja sākotnējo datu ir daudz, tie jāievada mašīnas
operatīvajā atmiņā pa daļām. Tālāk, lai aprēķinātu noviržu kvadrātu summas ![]() vai
vai ![]() , sākotnējie dati mašīnas operatīvajā atmiņā ir jāievada
otreiz, kas prasa daudz laika. Turpretī, izmantojot formulas (1.35) un (1.36),
vienā darba šūnā mašīnas atmiņā uzkrāj
, sākotnējie dati mašīnas operatīvajā atmiņā ir jāievada
otreiz, kas prasa daudz laika. Turpretī, izmantojot formulas (1.35) un (1.36),
vienā darba šūnā mašīnas atmiņā uzkrāj ![]() , otrā
, otrā ![]() , resp.,
, resp., ![]() un
un ![]() . Ar šīm summām pietiek, lai aprēķinātu gan aritmētisko
vidējo, gan dispersiju, neatgriežoties pie sākotnējiem datiem.
. Ar šīm summām pietiek, lai aprēķinātu gan aritmētisko
vidējo, gan dispersiju, neatgriežoties pie sākotnējiem datiem.
Šīs
summas viegli fiksēt arī pa kopas daļām (starpsummas). Tas ļauj viegli
aprēķināt iepriekš izraudzīto grupu aritmētiskos vidējos un dispersijas.
Piemēri.
1.
Aprēķinām darba algas dispersiju 8 strādnieku brigādei, kas bija aplūkota
1.2.3. paragrāfā. Jāsastāda tabula 1.8.:
1.8.tabula
Darba tabula dispersijas aprēķināšanai, izmantojot novēroto datu nu to
kvadrātu summas.
|
Novērojumu Nr. |
Novērotie
dati x un to summa |
Novēroto
datu kvadrāti x2 un to summa |
|
1. 2. 3. 4. 5. 6. 7. 8. |
215,27 230,91 190,15 250,31 201,50 222,93 219,10 205,12 |
46
341 53
319 36
157 62
655 40
602 49
698 48
005 42
074 |
|
|
1735,29= |
378
851= |
s2=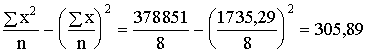 .
.
Aprēķinātā
dispersija sakrīt ar rezultātu, kurš tika iegūts iepriekš (1.3.1.§), ja
neskaita nelielas atšķirības starprezultātu noapaļošanas dēļ. Ja darbu izpilda
ar vienādu zīmīgo ciparu skaitu, tad par precīzāko ir jāatzīst tas rezultāts,
kurš iegūts izpildot darbības bez liela zīmīgo ciparu skaita zuduma
starprezultātos. Liels zīmīgo ciparu skaita zudums, strādājot ar formulām
(1.35) vai (1.36) rodas, izdarot pēdējo atņemšanas darbību. Tādēļ par precīzāko
piemēra ietvaros ir jāatzīst dispersija, kas aprēķināta 1.3.1.§. Lai
iegūtu to pašu precizitāti ar formulām (1.35) un (1.36) ir jāizmanto aprēķinos
lielāks zīmīgo ciparu skaits.
2.
Aprēķināsim graudaugu ražības dispersiju pirmās ekoloģiskās grupas saimniecībām.
Sākotnējo datu sagatavošana ir parādīta 1.11 tabulā kompleksu aprēķinu
ietvaros. Vajadzīgās summas ņem no tās: ![]() =2248;
=2248; ![]() =52768;
=52768; ![]() =100.
=100.
Tad s2=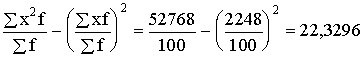 .
.
Šajā
piemērā, kā redzams, tika izmantota formula (1.36), kura paredz statistisko
svaru lietošanu. Piemērā statistiskie svari ir jāizmanto tādēļ, ka dispersiju
rēķina pēc iepriekš sagrupētiem datiem (variācijas rindas).
1.3.3. Intragrupu un starpgrupu dispersijas
Grupēšana
ir statistikas datu apstrādes pamatmetode. Matemātiski tālāk apstrādājot
grupējuma rezultātus, vispirms aprēķina aritmētiskos vidējos katrai grupai.
Grupu vidējo lielumu aprēķināšana tehniski ne ar ko neatšķiras no visas kopas
vidējo lielumu aprēķināšanas, vienīgi jāsummē nevis pa visu kopu, bet pa katru
grupu atsevišķi. Summu dala nevis ar visas kopas, bet gan grupas vienību skaitu
vai grupas statistisko svaru summu, ja rēķina svērto vidējo. Grupu aritmētiskos
vidējos parasti sakārto tabulā.
Bez vidējā lieluma katrai
grupai var aprēķināt arī variācijas rādītājus: dispersiju, standartnovirzi u.c.
Lai
raksturotu pazīmes variāciju pa grupām, katrai grupai aprēķina grupas
dispersiju ![]() , kur i - grupas
numurs. Izmanto formulas:
, kur i - grupas
numurs. Izmanto formulas:
vienkāršai dispersijai
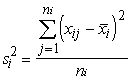 ; (1.37)
; (1.37)
svērtai dispersijai
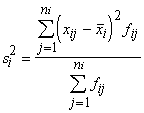 , (1.38)
, (1.38)
kur xij - i-tās grupas j-tā vērtība;
![]() - i-tās grupas
aritmētiskais vidējais;
- i-tās grupas
aritmētiskais vidējais;
ni - i-tās grupas vienību skaits;
fij - i-tās vienības statistiskais svars; šī vienība atrodas
i-tajā grupā.
Summēšana notiek grupu robežās.
Kad ir aprēķinātas atsevišķas
grupu dispersijas, var atrast visu grupu vidējo dispersiju ![]() :
:
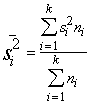 , (1.39)
, (1.39)
kur k - grupu skaits. Jāsummē pa visām grupām, i=1; 2; …;
k. Ja izmanto statistisko svaru summas, formula ir šāda:
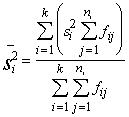 . (1.40)
. (1.40)
Grupu
dispersiju aritmētisko vidējo sauc par intragrupu dispersiju (arī par grupu
iekšējo dispersiju), jo tā rāda variāciju, kādā vidēji ir izdalītajās grupās.
Intragrupu
dispersija ir mazāka par kopējo jeb parastu dispersiju s2, ko
aprēķina pēc formulām (1.29); (1.30); (1.35); (1.36), jo grupu aritmētiskie
vidējie ![]() nesakrīt ar visas
kopas aritmētisko vidējo
nesakrīt ar visas
kopas aritmētisko vidējo ![]() un individuālo datu
novirzes no grupas vidējiem caurmērā ir mazākas nekā novirzes no visas kopas
aritmētiskā vidējā.
un individuālo datu
novirzes no grupas vidējiem caurmērā ir mazākas nekā novirzes no visas kopas
aritmētiskā vidējā.
Ir
svarīgi noteikt ne vien intragrupu, bet arī starpgrupu jeb intergrupu dispersiju.
Tā raksturo grupu aritmētisko vidējo variāciju ap visas kopas aritmētisko
vidējo. Starpgrupu dispersiju apzīmē ar simbolu d2. To var
aprēķināt pēc formulas (1.41) kā grupu aritmētisko vidējo ![]() dispersiju, par
svariem izmantojot kopas vienību skaitu katrā grupā:
dispersiju, par
svariem izmantojot kopas vienību skaitu katrā grupā:
d2=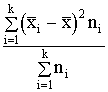 . (1.41)
. (1.41)
Ja grupu aritmētisko vidējo
aprēķināšanā ir izmantoti citi statistiskie svari, kas ir atšķirīgi no kopas
vienību skaita, tad jālieto formula (1.42):
d2=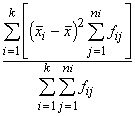 . (1.42)
. (1.42)
Piemērs.
Brigādē
strādā 5 strādnieki un 3 mācekļi. Strādnieku darba ražīgums ir 10; 12; 8; 13; 7
izstrādājumi stundā, bet mācekļu - attiecīgi 6; 8; 10 izstrādājumi stundā.
Vidējā izstrāde visiem strādājošiem ir 9,25 izstrādājumi stundā, dispersija s2=2,2776
izstrādājumi. Pēdējie rādītāji var būt nepietiekami, jo strādnieku grupā
izstrāde parasti ir augstāka nekā mācekļu grupā. Tādēļ aprēķināsim vidējos un
variācijas rādītājus atsevišķi strādniekiem (indekss 1) un mācekļiem (indekss
2), kā arī intragrupu un starpgrupu dispersijas.
Vidējie lielumi:
![]() (izstrādājumi);
(izstrādājumi);
![]() (izstrādājumi).
(izstrādājumi).
Grupu dispersijas aprēķina pēc formulas (1.37):
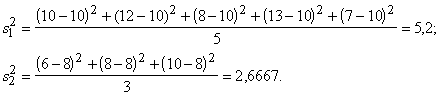
Abu grupu vidējo dispersiju jeb
intragrupu dispersiju aprēķina pēc formulas (1.39) :
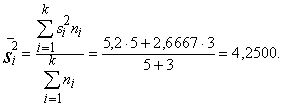
Intragrupu dispersija 4,25 ir
mazāka nekā kopējā dispersija 5,1875, jo darba ražīgums katras strādājošo
grupas ietvaros ir mazāk svārstīgs nekā visu strādājošo kopā.
Beidzot aprēķināsim starpgrupu
dispersiju, izmantojot formulu (1.41):
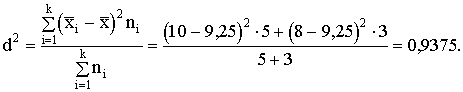
Šī dispersija raksturo grupu
vidējo lielumu variāciju ap kopējo vidējo. Redzam, ka grupu ietvaros variācija
tomēr ir lielāka nekā starp grupām. Tālāko uzdevumu - noskaidrot, vai
intragrupu un starpgrupu dispersijas atšķiras būtiski un līdz ar to vai darba
ražīgums strādnieku grupā ir būtiski augstāks nekā mācekļu grupā, risina
dispersijas analīze, kurai grāmatā ir veltīta atsevišķa nodaļa.
Ja ir aprēķināta kopējā
dispersija un intragrupu dispersija, starpgrupu dispersiju var atrast arī kā
pirmo divu dispersiju starpību. Tas izriet no dispersiju saskaitīšanas
teorēmas, kura apskatīta nākošajā paragrāfā.
1.3.4. Dispersiju saskaitīšanas teorēma
Intragrupu un starpgrupu
dispersiju summa ir vienāda ar kopējo dispersiju:
![]() . (1.43)
. (1.43)
Pierādījums.
Pieņemam, ka kopa sadalīta k
grupās, kurās ir n1, n2, n3, …, nk
vienības un ![]() .
.
Grupu aritmētiskos vidējos
aprēķina pēc formulas
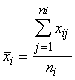 , (a)
, (a)
kopējo aritmētisko vidējo -
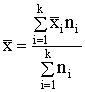 . (b)
. (b)
Grupu dispersijas var
aprēķināt, izmantojot pārveidoto dispersijas aprēķināšanas formulu:
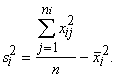 (c)
(c)
No šejienes
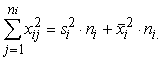 (d)
(d)
Ja šāda
sakarība ir spēkā katrai grupai atsevišķi, tad tai ir jābūt spēkā arī visām
grupām kopā. Tādēļ varam izdarīt šo izteiksmju summēšanu pēc indeksa i:
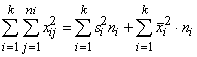 . (e)
. (e)
Vienādības (e) kreiso pusi
dalām ar n, bet labo - ar ![]() (to var darīt, jo n=
(to var darīt, jo n=![]() ):
):
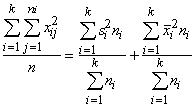 . (f)
. (f)
No vienādības (f) abām pusēm
atņem izteiksmi 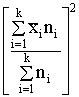 :
:
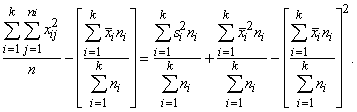 (g)
(g)
Ievērojot dispersijas
aprēķināšanas formulu (1.35):
s2=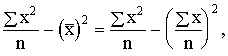
novērtējam pārveidoto vienādību
(g). Tās kreisā pusē ir kopējā dispersija s2, jo 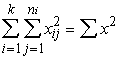 (dažādās formulās ir
izmantota vienīgi dažāda precizitāte indeksu norādēs) un
(dažādās formulās ir
izmantota vienīgi dažāda precizitāte indeksu norādēs) un 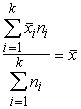 , jo kopējo vidējo var aprēķināt kā vidējo no grupu
aritmētiskajiem vidējiem, pēdējos sverot ar grupu vienību skaitu. Labās puses
pirmais saskaitāmais ir grupu dispersiju vidējais lielums
, jo kopējo vidējo var aprēķināt kā vidējo no grupu
aritmētiskajiem vidējiem, pēdējos sverot ar grupu vienību skaitu. Labās puses
pirmais saskaitāmais ir grupu dispersiju vidējais lielums ![]() . Divu pēdējo lielumu starpība ir starpgrupu dispersija d2
(par variējošo lielumu ir uzskatīti grupu vidējie lielumi
. Divu pēdējo lielumu starpība ir starpgrupu dispersija d2
(par variējošo lielumu ir uzskatīti grupu vidējie lielumi ![]() un, aprēķinot
dispersiju, ņemti vērā grupu īpatsvari). Līdz ar to sakarība (1.43)
un, aprēķinot
dispersiju, ņemti vērā grupu īpatsvari). Līdz ar to sakarība (1.43)
![]()
ir pierādīta.
Pierādītā
formula ir viena no fundamentālām matemātiskās statistikas sakarībām. Tiešā vai
pārveidotā veidā to izmanto daudzās matemātiskās statistikas nodaļās.
Pārbaudām
dispersiju saskaitīšanas teorēmas pareizību, izmantojot iepriekšējā paragrāfa
piemēru:
5,1875=4,2500+0,9375.
Tādējādi,
ja divas no trim savstarpēji saistītajām dispersijām ir aprēķinātas, trešo var
aprēķināt, izmantojot formulu (1.43), kas atvieglo skaitļošanas darbu.
Ja
salīdzina formulas (1.29); (1.35); (1.39); (1.40), tad ir redzams, ka visas
dispersijas aprēķina, dalot noviržu kvadrātu summas (kas ir dažādas) ar vienu
un to pašu kopas vienību skaitu ![]() vai svaru summu
vai svaru summu 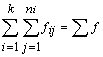 . Tādēļ vienādības (1.43) abas puses var pareizināt ar n,
resp.,
. Tādēļ vienādības (1.43) abas puses var pareizināt ar n,
resp., ![]() , un secināt, ka arī noviržu kvadrātu summas veido analogu
sakarību:
, un secināt, ka arī noviržu kvadrātu summas veido analogu
sakarību:
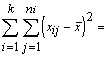
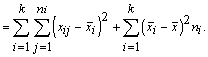
Vienkāršojot pierakstu,
iegūstam
![]() (1.44)
(1.44)
Arī šī
ir viena no fundamentālām matemātiskās statistikas sakarībām, ko izmanto,
piemēram, dispersijas analīzē.
1.4. Variācijas rindas momenti
1.4.1. Momentu jēdziens
Moments ir
jēdziens, ko plaši lieto mehānikā, lai raksturotu mehāniskai sistēmai pielikta
spēka iespējas sistēmu iekustināt un it īpaši izraisīt rotācijas kustību. Ir
zināms, ka spēka iespējas iekustināt mehānisku sistēmu ir atkarīgas no spēka
lieluma un no attāluma starp spēka pielikšanas un sistēmas atbalsta punktiem.
Līdzīgā
nozīmē terminu “moments” izmanto statistikā. Pieliktie spēki šajā gadījumā ir variācijas rindas intervālu
biežumi, bet spēku pielikšanas attālumi - intervālu centru attālumi no kāda
noteikta atskaites punkta.
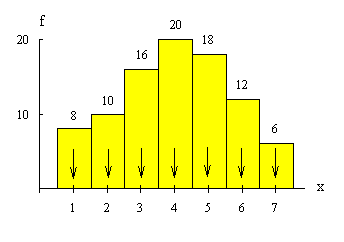
1.4.
attēls. Momentu ģeometriska interpretācija.
1.4.
attēlā ir parādīta histogramma, kuras stabiņus var uzlūkot par masīviem
ķermeņiem, kuri ar zināmu spēku spiež uz abscisu asi. Spēks ir proporcionāls
kopas vienību skaitam fi katrā intervālā, resp., stabiņā.
Iedomāsimies, ka abscisu ass ir atbalstīta kādā vienā punktā. Lai noteiktu, vai
pieliktais spēks izkustinās histogrammai analogu masīvu ķermeni, ir jānosaka
šis atbalsta punkts, resp., jāizvēlas kāds attālumu mērīšanas sākumpunkts. Par
tādu var izvēlēties
koordinātu sistēmas sākumpunktu;
jebkuru brīvi izvēlētu punktu uz abscisu ass;
aritmētisko vidējo.
Ja
histogrammai atbilstošs masīvs ķermenis ir atbalstīts punktā, kas atbilst
aritmētiskajam vidējam, pieliktie spēki savtarpēji līdzsvarojas un iedomātais
ķermenis var saglabāt līdzsvaru.
Atkarībā
no attālumu atskaites punkta izšķir sākuma momentus, nosacītos momentus un
centrālos momentus.
Kā
redzējām statistiskos momentus visvieglāk izprast un interpretēt, izmantojot
intervālu variācijas rindu un tās grafisko attēlu (histogrammu). Tomēr
statistiskos momentus tāpat kā vidējos lielumus var aprēķināt arī tieši no
sākotnējiem nesagrupētiem datiem. Sākotnējo datu tieša apstrāde turklāt dod
precīzākus momentu rādītājus. Vai šādā gadījumā ir vai nav jālieto statistiskie
svari, izšķir, vadoties no tādiem pat apsvērumiem, kā rēķinot aritmētisko
vidējo.
1.4.2. Variācijas rindas momentu definīcija un
pamatformulas
Par variācijas
rindas momentiem statistikā sauc datu (variantu) noviržu pakāpju
vidējos lielumus.
Novirzes
var ņemt no koordinātu sākumpunkta, no brīvi izvēlēta punkta un no aritmētiskā
vidējā. Līdz ar to iegūst attiecīgi sākuma momentus, nosacītos momentus un
centrālos momentus.
Novirzes
var ņemt pirmajā pakāpē ![]() , bet var pirms summēšanas kāpināt kādā citā pakāpē,
piemēram, kvadrātā. Līdz ar to iegūst dažādu kārtu jeb pakāpju momentus.
Statistikā biežāk lieto pirmās un otrās kārtas momentus,
retāk - trešās un ceturtās kārtas momentus. Sistēmas
dēļ aplūko arī nulltās kārtas momentus. Momentu pamatveidi, to pamatformulas
parādītas 1.9.tabulā.
, bet var pirms summēšanas kāpināt kādā citā pakāpē,
piemēram, kvadrātā. Līdz ar to iegūst dažādu kārtu jeb pakāpju momentus.
Statistikā biežāk lieto pirmās un otrās kārtas momentus,
retāk - trešās un ceturtās kārtas momentus. Sistēmas
dēļ aplūko arī nulltās kārtas momentus. Momentu pamatveidi, to pamatformulas
parādītas 1.9.tabulā.
1.9.tabula
Variācijas rindas momentu veidi un pamatformulas
|
Momentu kārta |
Sākuma
M |
Nosacītie
m |
Centrālie
|
|
Nulltā |
|
|
|
|
Pirmā |
|
|
|
|
Otrā |
|
|
|
|
Trešā |
|
|
|
|
Ceturtā |
|
|
|
k-tās kārtas momentus
vispārīgā veidā definē, izmantojot šādas formulas:
sākuma momenti
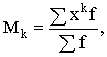 (1.45)
(1.45)
nosacītie momenti
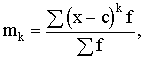 (1.46)
(1.46)
centrālie momenti
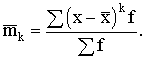 (1.47)
(1.47)
Momentu
apzīmēšanai bieži lieto arī citus terminus un simbolus.
Aprēķinot
momentus, par statistiskajiem svariem f var ņemt gan absolūtos, gan relatīvos
biežumus.Apstrādājot iepriekš nesagrupētus datus, katra kopas vienība nosacīti
veido savu grupu ar biežumu f = 1. Ja statistisko momentu formēšanā no
profesionālās analīzes viedokļa visi novērojumi ir vienādi nozīmīgi, resp.,
“lieli”, tad visi f = 1, un tos var formulā svītrot, ievērojot, ka tādā
gadījumā ![]() =n.
=n.
Nulltās
kārtas momenti jebkurai variācijas rindai ir vienādi ar 1, jo
jebkurš skaitlis nulltajā pakāpē vienāds ar 1 un arī 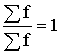 . Šiem momentiem nav praktiskas nozīmes.
. Šiem momentiem nav praktiskas nozīmes.
1.4.3. Pirmās kārtas momentu īpašības
Pirmās
kārtas sākuma moments ir variācijas rindas aritmētiskais vidējais. Tas
ir tieši redzams no formulas
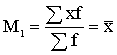 vai
vai ![]() , ja visi f=1.
, ja visi f=1.
Pirmās
kārtas nosacīto momentu var izmantot aritmētiskā vidējā lieluma
izskaitļošanas vienkāršošanai, kā tas izriet no aritmētiskā vidējā īpašībām:
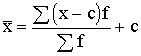 vai
vai ![]()
Pirmās
kārtas centrālais moments ir vienāds ar 0. No aritmētiskā vidējā
īpašības redzams, ka noviržu algebriskā summa no aritmētiskā vidējā ir vienāda
ar nulli: ![]() vai arī
vai arī ![]() , no kā izriet, ka
, no kā izriet, ka ![]()
Līdz ar
to no pirmās kārtas momentiem ekonomiska interpretācija ir tikai sākuma
momentam, kurš ir variācijas rindas aritmētiskais vidējais.
1.4.4. Otrās kārtas momentu īpašības
Otrās
kārtas centrālais moments, kā redzams no formulas, ir
variācijas rindas dispersija. Tātad otrās kārtas centrālais moments
raksturo pazīmes variāciju.
Otrās
kārtas sākuma momentus var izmantot dispersijas aprēķināšanas
atvieglošanai. No iepriekšējām nodaļām zinām, ka
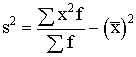
vai
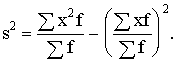 (sk.1.36)
(sk.1.36)
Pēdējās
formulas labajā pusē pirmais loceklis ir otrās kārtas sākuma moments M2,
bet otrais loceklis - pirmās kārtas sākuma momenta M1 kvadrāts. Pati
dispersija ir otrās kārtas centrālais moments. Tādēļ
![]() (1.48)
(1.48)
Otrās
kārtas centrālo momentu var aprēķināt, izmantojot arī otrās kārtas nosacīto
momentu un pirmās kārtas nosacītā momenta kvadrātu.
![]() (1.49)
(1.49)
Skaitļošanu
var vēl tālāk vienkāršot, ja datus dala ar intervāla vienību ![]() .Tad
.Tad
![]() , (1.50)
, (1.50)
kur m2 un m1
ir ![]() reizes samazināto datu
nosacītie momenti.
reizes samazināto datu
nosacītie momenti.
Rēķinot
nosacītos momentus, atskaites sākumu var izvēlēties brīvi, tikai vienas
formulas ietvaros to nedrīkst mainīt.
1.4.5. Vispārinājumi
Statistikā
svarīgākā nozīme ir pirmās kārtas sākuma momentam un augstāko kārtu
centrālajiem momentiem. Pirmās kārtas sākuma moments ir aritmētiskais vidējais,
bet otrās kārtas centrālais moments ir dispersija. Turpmāk parādīsim, ka no
trešās kārtas centrālā momenta iegūst asimetrijas, bet no ceturtās kārtas
centrālā momenta - ekscesa rādītājus.
Sākuma
momentus un nosacītos momentus lieto kā starprezultātus centrālo momentu
aprēķināšanai. Izmantojot datoru, nav grūti izpildīt darbības ar lieliem
skaitļiem, tāpēc rēķina sākuma momentus.
Centrālos
momentus iegūst no nosacītajiem momentiem, izmantojot šādas formulas (dažas no
tām iepriekš pamatotajām):
![]() = 1;
= 1;
![]() = 0;
= 0;
![]() = m2-
= m2-![]() ; (1.51)
; (1.51)
![]() ;
;
![]() .
.
Formulās
(1.51) nosacīto momentu vietā var ņemt sākuma momentus, jo nosacīto momentu
aprēķināšanas formulā var likt c=0. Parasti tā arī dara.
1.4.6. Momentu aprēķināšanas piemēri
1.2.tabulā
bija dotas variācijas rindas: pirmās un otrās ekoloģiskās grupas saimniecību un
graudaugu sējumu platību sadalījumi pēc graudaugu ražības. Aprēķināsim abiem šiem
sadalījumiem pirmo četru kārtu momentus. Pirmās variācijas rindas momentu
aprēķinu tehniku parādīsim pilnīgi, bet otrai variāciju rindai dosim gatavus
rezultātus. Lai gūtu iespēju salīdzināt aprēķinātos rādītājus un tos novērtēt,
abi uzdevumi tiek risināti vienlaikus. Novērtējot tos rādītājus, kuriem ir
iespējama tieša ekonomiska interpretācija, ir lietderīgi izmantot abu
sadalījuma rindu grafiskos attēlus, kuri redzami 1.3. attēlā.
Pirms
aprēķinu uzsākšanas mums vēlreiz jāatgriežas pie jautājuma par statistisko
svaru izvēli. Jautājums par statistisko svaru izvēli momentu aprēķinos
statistikas teorijā līdz galam nav atrisināts. Rēķinot aritmētisko vidējo, kas
vienlaikus ir pirmās kārtas sākuma moments, vienprātīgi tiek ieteikts izmantot
svarus, kuri nodrošina summu ![]() un
un ![]() reālu ekonomisku
saturu. Piemēram, rēķinot vidējo ražību, par statistiskajiem svariem ir
jāizmanto sējumu platības. Rēķinot otrās kārtas centrālo momentu, kas
vienlaikus ir variācijas rindas dispersija, vairums autoru saglabā to pašu
svaru sistēmu. Turpretī, rēķinot augstāku kārtu momentus, gandrīz visās mācību
grāmatās bez īpaša pamatojuma tiek izmantots kopas vienību (novērojumu) skaits.
reālu ekonomisku
saturu. Piemēram, rēķinot vidējo ražību, par statistiskajiem svariem ir
jāizmanto sējumu platības. Rēķinot otrās kārtas centrālo momentu, kas
vienlaikus ir variācijas rindas dispersija, vairums autoru saglabā to pašu
svaru sistēmu. Turpretī, rēķinot augstāku kārtu momentus, gandrīz visās mācību
grāmatās bez īpaša pamatojuma tiek izmantots kopas vienību (novērojumu) skaits.
Dažādu
statistisko svaru izmantošana zemāko un augstāko kārtu momentu aprēķinos noved
pie tā, ka vairs nav spēkā aplūkotās momentu sakarības. Tādēļ tāda rīcība nav
ieteicama. Reiz izvēlētā statistisko svaru sistēma ir jāsaglabā.
Pēc
mūsu domām, izvēloties statistisko svaru sistēmu, varētu vadīties no šādiem apsvērumiem.
1.
Analīzē svarīgākais ir aritmētiskais vidējais, kurš jāaprēķina maksimāli
precīzi. Augstāko kārtu momenti veido papildinformāciju. Tad statistiskie svari
ir jāizvēlās atbilstoši iepiekš aprādītajiem nosacījumiem. Piemēram, rēķinot
vidējo ražību, svaru sistēmu veido sējumu platības. saglabājot šo svaru sistēmu
augstāko kārtu momentu aprēķinos, interpretācijā jāievēro, ka esam raksturojuši
nevis saimniecību, bet sējumu platību sadalījuma pēc ražības variāciju,
asimetriju un ekscesu.
2.
Analīzē svarīgākais ir izpētīt tieši kopas vienību(saimniecību) nevis sējumu
platību sadalījuma īpašības. Precīza aritmētiskā vidējā sasaiste ar
absolūtajiem un relatīvajiem lielumiem nav obligāta. Tad par statistiskajiem
svariem varam izvēlēties variācijas rindas absolūtos vai relatīvos biežumus. Ja
visas kopas vienības ir kvalitatīvi vienveidīgas un to ir daudz, aritmētiskais
vidējais parasti iegūst pilnīgi pieņemamu tuvinājumu un ērtāka ir citu
variācijas rindas raksturotāju interpretācija.
Tā kā
ražības analīzē izšķiroša nozīme ir vidējam lielumam un to iepriekš
aprēķinājām, izmantojot par statistiskajiem svariem sējumu platību īpatsvarus,
šo svaru sistēmu saglabāsim arī turpmāk. Līdz ar to jāievēro, ka īstenībā
pētījam nevis saimniecību, bet gan sējumu platību sadalījumu pēc ražības5.
Satistikā
visvairāk vajadzīgos centrālos momentus var aprēķināt vai nu tieši, vai
iepriekš kā starprezultātus aprēķinot sākuma momentus, vai nosacītos momentus6.
1.10.
tabula
Centrālo momentu tieša aprēķināšana ar noviržu metodi pirmās ekoloģiskās
grupas saimniecību sējumu platību sadalījumam pēc graudaugu ražības ![]() .
.
|
x |
x- |
f |
|
|
|
|
|
12 16 20 24 28 32 |
-10,48 -6,48 -2,48 1,52 5,52 9,52 |
2 16 30 28 18 6 |
-20,96 -103,68 -74,40 42,56 99,36 57,12 |
219,6608 671,8464 184,5120 64,6912 548,4672 543,7824 |
-2302,0451 -4353,5646 -457,5898 98,3306 3027,5389 5176,8084 |
24
125,432 28
211,098 1
134,823 149,463 16
712,014 49
283,215 |
|
Kopā |
´ |
100 |
+199,04
0 |
2232,9600 |
+8302,6779
+1189,4784 |
119
616,040 |
________________________
5 Vispārējā gadījumā ģeometriskās ilustrācijas nolūkā
vajadzētu izgatavot arī citu attēlu, kurš var atšķirties no attēla 1.3.
Konkrētajā uzdevumā abi sadalījumi ir samērā līdzīgi. Abu attēlu atšķirība
vizuāli grūti pamanāma. Tādēļ turpināsim izmantot 1.3. attēlu.
6 Tāpat kā aprēķinot aritmētisko vidējo, arī visu pārējo
momentu vērtības ir precīzākas, ja tās aprēķina pēc sākotnējiem, nesagrupētiem
datiem.
1.11
tabula
Sākuma momentu aprēķināšana pirmās ekoloģiskās grupas saimniecību sējumu
platību sadalījumam pēc graudaugu ražības.
|
x |
|
|
|
f |
xf |
x2f |
x3f |
x4f |
|
12 16 20 24 28 32 |
144 256 400 576 784 1 024 |
1 728 4 096 8 000 13
824 21
952 32
768 |
20
736 65
536 160
000 331
776 614
656 1 048
576 |
2 16 30 28 18 6 |
24 256 600 672 504 192 |
288 4 096 12
000 16
128 14
122 6 144 |
3 456 65
536 240
000 387
072 395 136 196
608 |
41
472 1 048
576 4 800
000 9 289
728 11
063 808 6 291
456 |
|
Kopā |
´ |
´ |
´ |
100 |
2248 |
52 768 |
1 287 808 |
32 535 040 |
Centrālo
momentu tieša aprēķināšana ir parādīta 1.10. tabulā. Aprēķināšanas metodi, kas
atainota šai tabulā, var saukt par noviržu metodi. Tās trūkums ir tāds,
ka vispirms ir jāaprēķina aritmētiskais vidējais un novirzes no tā.
Centrālos
momentus aprēķina, izmantojot 1.9. tabulas pēdējā ailē parādītās formulas:
![]()
![]()
![]() ;
;
![]()
No
centrālajiem momentiem tieša ekonomiska interpretācija ir otrās kārtas
momentam, kurš vienlaikus ir sadalījuma dispersija. Pirmajā ekoloģiskajā grupā ![]() otrajā - 22,5584. Abas
dispersijas pēc noapaļošanas ir praktiski vienādas. Aprēķinot kvadrātsakni no
dispersijas, iegūst standartnovirzi jeb vidējo kvadrātisko novirzi, kura pēc
noapaļošanas abās grupās ir 4,7 cnt/ha.
otrajā - 22,5584. Abas
dispersijas pēc noapaļošanas ir praktiski vienādas. Aprēķinot kvadrātsakni no
dispersijas, iegūst standartnovirzi jeb vidējo kvadrātisko novirzi, kura pēc
noapaļošanas abās grupās ir 4,7 cnt/ha.
Dati sākuma
momentu aprēķināšanai ir izskaitļoti un parādīti 1.11. tabulā. Tabulas
aiļu virsraksti vienlaikus uzskatāmi par formulām, kuras jāizmanto to
aizpildīšanai. Izmantojot šīs tabulas datus un iepriekš minētās formulas, var
izskaitļot vispirms sākuma momentus, bet izmantojot tos kā starprezultātus, var
atrast centrālos momentus. Lai neuzkrātos skaitļošanas kļūdas, starprezultāti
kā vienmēr jāfiksē ar pietiekami lielu zīmīgo ciparu skaitu. Gala rezultāti
ekonomiskajā interpretācijā jānoapaļo līdz tādai precizitātei, kādu nodrošina
sākotnējie dati.
Sākuma dati:
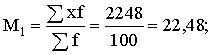
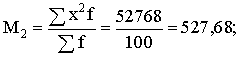
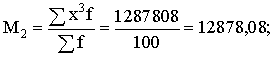
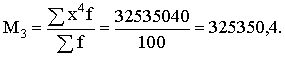
Centrālie momenti:
![]()
![]()
![]()
![]()
![]()
![]() .
.
Redzam,
ka centrālie momenti, kurus aprēķinājām izmantojot kā starprezultātus sākuma
momentus, samērā precīzi sakrīt ar centrālajiem momentiem, kurus aprēķinājām ar
t.s. noviržu metodi. Nelielas atšķirības pēdējos zīmīgajos ciparos
izskaidrojamas ar starprezultātu noapaļošanu. Ja abos gadījumos darbs izpildīts
ar vienu un to pašu zīmīgo ciparu skaitu, par precīzākiem jāuzlūko rezultāti,
kuri iegūti ar metodi, kuras realizācija prasa izpildīt mazāk skaitļošanas
operāciju un darbu veic ar mazākiem skaitļiem.
Atcerēsimies,
ka pirmās kārtas sākuma moments ir aritmētiskais vidējais. Pirmās ekoloģiskās
grupas saimniecībās 22,48 (otrās - 20,04). Citiem sākuma momentiem tieša
statistiska satura nav. Tos ērti izmantot kā starprezultātus centrālo momentu
aprēķināšanai īpaši tad, ja darbu veic ar datoru.
Otrās kārtas centrālais moments
ir dispersija.
Augstāko
kārtu centrāliem momentiem tiešas ekonomiskās interpretācijas nav, bet no tiem
viegli aprēķināt tālākos variācijas rindas raksturotājus: asimetrijas un
ekscesa rādītājus.
Nosacītos
momentus aprēķina un izmanto kā starprezultātus centrālo momentu aprēķināšanai
ja darbu izpilda ar nelielas jaudas skaitļošanas tehniku. Nosacītie momenti dod
iespēju strādāt ar “mazākiem” skaitļiem, bet lietojamās formulas ir nedaudz
sarežģītākas. Tā kā patreiz lietojamās skaitļošanas mašīnas bez grūtībām
izpilda darbības ar daudzzīmju skaitļiem, nosacītie momenti zaudē praktisku
nozīmi. Tādēļ attiecīgs piemērs šajā grāmatā nav parādīts7.
________________________
1 Vajadzības gadījumā nosacīto momentu
aprēķināšanas un izmantošanas piemērus var atrast autora mācību grāmatā
“Varbūtību teorija un matemātiskā statistika”. R.:1985.
1.4.7. Standartizētie momenti
Augstāko
kārtu momenti iegūst statistisku interpretāciju, ja tos standartizē. Par standartu
pieņem sadalījuma standartnovirzi s, t.i., kvadrātsakni no otrās kārtas
centrālā momenta ![]() . Tādā gadījumā standartizētos momentus aprēķina pēc
formulas
. Tādā gadījumā standartizētos momentus aprēķina pēc
formulas
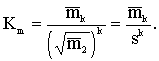 (1.52)
(1.52)
Standartizētos
momentus literatūrā diezgan bieži apzīmē ar mazo burtu r. Tas nav izdevīgi, jo
ar šo burtu vienmēr apzīmē korelācijas koeficientu.
Pirmo četru kārtu
standartizētie momenti ir šādi:
![]()
![]()
![]()
![]()
Pirmās
un otrās kārtas standartizētie momenti ir konstantes. Statistiska
interpretācija ir trešās un ceturtās kārtas standartizētajiem momentiem. Trešās
kārtas standartizētais moments ir asimetrijas koeficients, ceturtās kārtas
standartizēto momentu izmanto ekscesa koeficienta aprēķināšanai.
1.5. Asimetrijas un ekscesa rādītāji
1.5.1. Momentu asimetrijas un ekscesa koeficienti
Visbiežāk
lietotie asimetrijas un ekscesa rādītāji ir trešās un ceturtās kārtas
standartizētie momenti. Trešās kārtas standartizēto momentu K3 sauc
par asimetrijas
koeficientu:
![]() (1.54)
(1.54)
Ja
sadalījums ir simetrisks pret aritmētisko vidējo, asimetrijas koeficients K3
ir vienāds ar 0. Ja koeficients nav vienāds ar 0, sadalījums ir vairāk vai
mazāk asimetrisks. Asimetrija ir lielāka, ja lielāka ir koeficienta absolūtā
vērtība. Koeficienta zīme rāda asimetrijas virzienu.
Ja
sadalījuma kreisā puse, kura atbilst pazīmes mazākajām vērtībām, ir izstiepta,
bet labā puse aprauta, asimetrijas koeficients ir negatīvs un otrādi.
Asimetrijas un ekscesa rādītāji
piemēriem.
![]()
|
Pirmai ekoloģiskai grupai
|
Otrai ekoloģiskai grupai
|
Kā rāda
trešās kārtas standartizētie momenti (asimetrijas koeficienti), abiem
sadalījumiem ir neliela pozitīvā asimetrija - izstiepts labais, bet aprauts
kreisais zars. Atgriežoties pie 1.3 grafiskā attēla, var pārliecināties, ka
histogrammai, kura attēlo otrās ekoloģiskās grupas saimniecību sadalījumu, šī
īpašība ir izteiktāka, tādēļ asimetrijas koeficients ir lielāks. Pilnīgi
simetriskam sadalījumam asimetrijas koeficients ir nulle. Abi piemēram
izmantotie sadalījumi ir samērā tuvi simetriskam, īpaši pirmais.
Ceturtās
kārtas standartizēto momentu K4 tieša izmantošana nav ērta, jo
normāla ekscesa gadījumā K4 nav 0, bet 3. Tādēļ praksē biežāk
izmanto ekscesa koeficientu, ko aprēķina ar formulu
![]() (1.55)
(1.55)
Ekscesa
koeficienta skaitlisko lielumu novērtē, salīdzinot to ar normālā sadalījuma
koeficientu, kurš ir vienāds ar nulli.
Ja
empīriskais ekscesa koeficients ir lielāks par 0, tad sadalījums ir stāvāks,
kopas vienību koncentrācija ap vidējo lielāka nekā normālā sadalījuma gadījumā.
Ja ekscesa koeficients ir mazāks par 0, kopas vienību koncentrācija ap vidējo
ir mazāka nekā normālā sadalījuma gadījumā.
Atgriežoties
pie piemēra, redzam, ka abu sadalījumu ekscesa koeficienti ir mazāki par 0.
Pirmai grupai - 0,601 (2,399 - 3), otrai - 0,428 (2,572 - 3). Otrās grupas
sadalījums pēc ekscesa īpašības ir tuvāks normālam sadalījumam (attēlā
histogrammai ir nedaudz smailāka virsotne) nekā pirmās grupās. Kā novērtēt, vai
šīs atšķirības ir statistiski nozīmīgas, būs parādīts turpmāk.
Momentu
asimetrijas un ekscesa koeficienti nav lietojami, ja statistiskajā kopā ir t.s.
krasi
atšķirīgās vienības. Tādā gadījumā šo vienību datu novirzes no vidējā ![]() , kāpinātas kubā vai ceturtajā pakāpē, sastāda lielāko daļu
no attiecīgās noviržu pakāpju summas. Līdz ar to asimetrijas un ekscesa
rādītāju lielumu nosaka tikai šīs krasi atšķirīgās vienības. Tādā gadījumā
trešās un ceturtās kārtas standartizētie momenti pārstāj raksturot asimetriju
un ekscesu, bet atspoguļo vienkārši kopas neviendabību.
, kāpinātas kubā vai ceturtajā pakāpē, sastāda lielāko daļu
no attiecīgās noviržu pakāpju summas. Līdz ar to asimetrijas un ekscesa
rādītāju lielumu nosaka tikai šīs krasi atšķirīgās vienības. Tādā gadījumā
trešās un ceturtās kārtas standartizētie momenti pārstāj raksturot asimetriju
un ekscesu, bet atspoguļo vienkārši kopas neviendabību.
Ja
krasi atšķirīgās vienības no apstrādājamo datu kopas izslēgt nav vēlams vai nav
iespējams, sadalījuma asimetriju labāk raksturot ar struktūras asimetrijas
rādītājiem, kaut arī tie ir vienkāršāki nekā attiecīgie momentu raksturotāji.
1.5.2. Struktūras asimetrijas koeficienti
Struktūras
asimetrijas rādītājus aprēķina, savstarpēji salīdzinot aritmētisko
vidējo, modu un mediānu.
Ja
sadalījums ir simetrisks un ar vienu modālo lielumu, tad ![]() =Mo=Me. Aritmētiskais vidējais, moda un mediāna sakrīt.
=Mo=Me. Aritmētiskais vidējais, moda un mediāna sakrīt.
Attiecību
![]() (1.56)
(1.56)
var izmantot sadalījuma
simetrijas aptuvenai novērtēšanai. Simetriskam sadalījumam šī attiecība ir
vienāda ar nulli. Mēreni asimetriska sadalījuma gadījumā tā nepārniedz trīs.
Labākus
rezultātus dod struktūras asimetrijas koeficients, kuru aprēķinot izmanto
standartnovirzi. Struktūras asimetrijas koeficienta KA formula ir
šāda:
![]() . (1.57)
. (1.57)
Ja KA
> 0, sadalījuma histogrammai
labais zars izstiepts, bet kreisais - aprauts (pozitīva
asimetrija);
ja KA
< 0, sadalījuma histogrammai
kreisais zars iztiepts, bet labais - aprauts (negatīva
asimetrija);
ja KA
» 0, sadalījums ir tuva simetriskam.
Aprēķināsim
struktūras asimetrijas koeficientu pirmās ekoloģiskās grupas saimniecību
sadalījumam pēc graudaugu ražības. No iepriekšējiem aprēķiniem zinām, ka ![]() = 22,48, Mo = 21,5, s = 4,725. Tad
= 22,48, Mo = 21,5, s = 4,725. Tad
KA=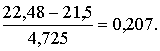
KA
= 0,207 > 0, līdz ar to jāsecina, ka sadalījumam ir izstiepts labais, bet
aprauts kreisais zars (sk. 1.3. grafisko attēlu). Lai spriestu, vai asimetrija
ir “liela” vai “maza”, ir nepieciešama zināma pieredze, kas uzkrājas, aprēķinot
asimetrijas koeficientus vairākiem sadalījumiem. Līdzīga pieredze ir vajadzīga,
lai ātri novērtētu arī citus koeficientus, piemēram, variācijas koeficientu.
Struktūras ekscesa rādītājus matemātiskajā statistikā nelieto.