2. Gadījumnotikumu varbūtības un darbības ar varbūtībām
2.1.
Pamatjēdzieni un definīcijas
2.1.1.
Notikumi varbūtību teorijas izpratnē
Ar
notikumu vabūtību teorijā saprot jebkuru faktu,
kuru var konstatēt novērojuma vai izmēģinājuma rezultātā.
Par
novērojumu vai izmēģinājumu
sauc zināmu apstākļu realizāciju, kā rezultātā var iestāties notikums. Izmēģinājums nozīmē aktīvu interesējošā apstākļu
kompleksa radīšanu. Novērojuma gaitā novērotājs pats šo apstākļu kompleksu
nerada. To rada vai nu dabas spēki vai citi cilvēki.
Par
droši sagaidāmu sauc notikumu, kas iestājas vienmēr,
ja ir izveidojusies zināma apstākļu kopa.
Par
neiespējamu sauc notikumu, kurš noteikti
neiestājas, ja ir izveidojusies zināma apstākļu kopa.
Par
gadījumnotikumu sauc notikumu, kurš, pastāvot zināmai
apstākļu kopai, var notikt un var arī nenotikt.
Notikumus
sauc par savienojamiem,
ja tie var notikt kopēji viena novērojuma vai izmēģinājuma rezultātā. Piemēram,
aptaujājot kārtējo pircēju, kas ienāk veikalā (izdarot novērojumu), izrādās, ka
tā ir sieviete (viens fakts jeb notikums) un latviete (otrs fakts jeb
notikums). Šie notikumi ir savstarpēji savienojami.
Notikumus
sauc par nesavienojamiem,
ja tie nevar notikt viena novērojuma vai izmēģinājuma rezultātā. Piemēram,
ņemot no nesašķirotu detaļu kastes vienu izstrādājumu, tas var būt vai nu
derīgs vai brāķis. Derīgas un brāķa detaļas paņemšana ir nesavienojami
notikumi.
Ja
ir zināms vai var iedomāties visus notikumus, no kuriem vismaz vienam ir
jārodas izmēģinājuma rezultātā, tad tie veido
pilnu notikumu kopu.
Piemēram,
izpildot loto spēles kartīti, jānosvītro
5 skaitļi. Ir iespējams pareizi nosvītrot 0, 1, 2, 3, 4, 5 skaitļus. Papildus
nosakot, ka kartīte izpildīta pareizi, citi notikumi nevar notikt. Uzrādītie
notikumi veido pilnu kopu.
Ja
pilnu notikumu kopu veido tikai divi nesavienojami notikumi, tad tos sauc par savstarpēji pretējiem, jeb alternatīviem. Alternatīvs
skatījums ir iespējams arī tad, ja pilnu kopu sākotnēji veido vairāki notikumi.
Piemēram, nesašķirotu detaļu kastē ir I, II un III šķiras derīgas detaļas un
nestandarta detaļas ar dažādiem defektiem. Ņemot vienu detaļu un novērtējot,
vai tā ir derīga, vai brāķis, realizējam alternatīvu
skatījumu. Šeit ir tikai divi savstarpēji nesavienojami notikumi.
Papildus fiksējot derīgas detaļas šķiru un brāķa detaļas defektu veidu,
alternatīvais skatījums zūd. Tad pilnu kopu veido vairāk nekā divi
nesavienojami notikumi.
Varbūtību
teorijā notikumus parasti apzīmē ar lielajiem latīņu burtiem A, B, C utt. Tiem pretējos notikumus apzīmē ar tādiem pat burtiem,
virs tiem liekot svītriņu: ![]()
Kodējot
apzīmējumus darbam ar datoru, izdevīgi izmantot skaitļu apzīmējumus.
Notikumus
sauc par vienādi iespējamiem,
ja novērojums vai izmēģinājums ir organizēts tā, lai visiem notikumiem būtu
objektīvi vienāda iespēja notikt katra izmēģinājuma rezultātā.
Šo
jēdzienu viegli pārprast, tādēļ tas jāpaskaidro plašāk.
Pieņemsim,
ka nesašķirotu detaļu kastē ir 90 derīgas un 10 brāķa detaļas. Ņemot nejauši
vienu detaļu, nevar cerēt, ka būs vienāda iespēja paņemt derīgu un brāķa
detaļu. Tas arī nav vajadzīgs. Lai notikumi būtu vienādi iespējami un lai
izmēģinājuma rezultātus varētu novērtēt ar varbūtību teoriju, ir jānodrošina,
lai būtu vienāda iespēja paņemt katru no kastē esošajām 100
detaļām. Runājot par vienādi iespējamiem notikumiem, pilna notikumu kopa šeit
nav jāsaprot kā sastāvoša no diviem notikumiem (derīga, vai nederīga detaļa),
bet no 100 notikumiem, iedomājoties ka detaļas numurētas.
Līdz
ar to ir lietderīgi no visiem notikumiem izdalīt elementāros
notikumus. Par
elementāriem sauc tādus notikumus, kurus nevar vairs tālāk detalizēt.
Piemēram, elementārs notikums būs nejauši paņemt no kastes 27-to detaļu. Paņemt
derīgu detaļu nav elementārs notikums, jo tas var notikt, paņemot jebkuru no 90
numurētām derīgām detaļām.
Vienādu
iespēju kā priekšnoteikumu parasti attiecina uz elementāriem notikumiem. Līdz
ar to neelementāru notikumu iestāšanās nav vienādi iespējama. Viņu iestāšanās
iespēju var noteikt skaitliski ar varbūtības palīdzību.
Praktiski
elementāru notikumu vienādu iespēju
nodrošina novērotāja
neitralitāte pret novērojuma rezultātiem. Šeit ir analoģija ar
izlases metodi. Turpinot piemēru, ir
jānodrošina, lai atlases izdarītājs ņemamo detaļu nenovērtētu vizuāli vai kā
citādi un apzināti vai neapzināti nedotu priekšroku derīgām vai brāķa detaļām.
Ja tādu iepriekšēju novērtēšanu izdara, novērojuma rezultātus vairs nevar
novērtēt ar varbūtību teorijas metodēm.
Par
iespējām sauc potenciālus notikumus, kas ir
pamats kāda reāla notikuma notikšanai. Turpinot piemēru par kasti ar 100
detaļām, tajā ir 90 iespējas paņemt derīgu detaļu un 10 iespējas paņemt brāķa
detaļu.
Izmantojot
iespēju jēdzienu, izveido klasisko vabūtības definīciju.
2.1.2. Vabūtības definīcijas
Varbūtība ir skaitlis, kas raksturo, cik droši
ir sagaidāma kāda notikuma notikšana. Bet šāds izteikums vēl nav varbūtības
definīcija.
Varbūtības
jēdzienu viegli uztvert intuitīvi, bet samērā grūti definēt precīzi, atklājot
šī jēdziena daudzpusīgos aspektus. Ir zināmas vairākas varbūtības definīcijas
un skaidrojumi. Katram no tiem ir savas priekšocības un savi trūkumi.
Visvecākā
un saprotamākā ir klasiskā varbūtības
definīcija. Tā balstās uz iespēju (potenciālu
notikumu) tiešu saskaitīšanu, iespēju skaitu pretstatot visam vienīgi iespējamo
notikumu skaitam.
Par
notikumam labvēlīgām iespējām sauc
tās iespējās, kas nodrošina šī notikuma notikšanu. Visbiežāk tie ir elementāri
notikumi iepriekš minētā izpratnē.
Piemēram,
traukā ir 100 loterijas biļetes, no
kurām 10 biļetēs ir atzīmēts laimests, bet pārējās ir tukšas. Tātad ir 10
labvēlīgas iespējas paņemt laimējošu biļeti no 100 iespējām pavisam.
Ja
labvēlīgo iespēju skaits ir zināms (piemērā 10) un ir zināms visu vienādi un
vienīgi iespējamo notikumu - iespēju skaits,
(piemērā 100), tad varbūtību var definēt šādi:
Par
notikuma A varbūtību sauc šim notikumam
labvēlīgo iespēju skaita M attiecību pret visu vienādi un vienīgi
iespējamo nesavienojamo, elementāro notikumu
skaitu N, kuri var rasties
viena izmēģinājuma vai
novērojuma rezultātā.
Varbūtību
apzīmē ar burtu P, aiz tā iekavās liekot gadījumnotikuma simbolu.
![]() . (2.1)
. (2.1)
Ja
uzdevumā operē tikai ar viena notikuma varbūtību, tad to var apzīmēt ar mazo p bez gadījuma notikuma simbola norādes.
Var
izmantot simbolus ![]() utt.
utt.
Varbūtību
laimēt piemēra ietvaros ir vienkārši izrēķināt. Tā kā pavisam traukā ir
100 lozes ( tās ir labi sajauktas un nav
iezīmētas), tātad visu ložu paņemšanas iespējas ir vienādas. Starp tām ir 10
labvēlīgas iespējas. Līdz ar to N = 100
un M = 10, no kā seko, ka
![]() .
.
Klasisko
varbūtību sauc arī par aprioro
varbūtību, jo to izrēķina pirms novērojuma vai izmēģinājuma uzsākšanas.
Klasiskās
varbūtības definīcijas galvenais trūkums
ir tās ierobežotās lietošanas iespējas. Lai lietotu šo definīciju un formulu
(2.1), ir iepriekš jāsaskaita visas iespējas un tajā skaitā - interesējošajam notikumam labvēlīgās
iespējas. To var izdarīt, organizējot dažādas izlozes un spēles, bet nevar
izdarīt ne dabas, ne sociālo zinātņu pētījumos. Piemērs, ka kastē ir 100
detaļas, no kurām 10 ir brāķis, ir samākslots. Ja detaļas būs pārbaudītas, tās
nekad atkal nesabērs vienā kastē. Tādēļ klasiskās varbūtības definīcijas
lietošanas apgabals aprobežojas ar dažādām loterijām un spēlēm.
Vēsturiski
varbūtību teorija arī ir radusies kā spēļu teorija, kaut gan tagad to lieto
gandrīz visās zinātnes nozarēs. Spēļu rīki un noteikumi vienmēr ir izstrādāti
tā, lai iepriekš varētu saskaitīt dažādu elementāru notikumu un iespēju skaitu,
kas nosaka spēles rezultātus.
Katram
spēļu automātam kādā slēptā vietā atrodas rokturis, ar kuru automāta īpašnieks
var nostādīt sev vēlamo peļņas normu.
Tehniski
pilnīgi iespējams, ka modernie spēļu automāti ir vadāmi no attāluma. Kamēr spēlētājs vēl nav iekarsis un
rūpīgi seko panākumiem, īpašnieks var peļņas normu ar tālvadības pulti nostādīt
tuvu nullei. Bet, kad spēlētāja galvā jau sakāpis viskijs un džins un viņš nonācis azartā, peļņas normu
var pacelt daudzkārt lielāku. Cits jautājums, kādā mērā likums šādas
manipulācijas atļauj un kā tās kontrolē.
Lai
spēļu uzņēmējdarbību padarītu rentablu, viss dažkārt sarežģītais spēles algoritms ir jāapraksta ar varbūtības
teorijas kategorijām un vajadzības gadījumā jāprogrammē.
Tā
kā spēļu situācijas ir pašas vienkāršākās un tur var pielietot klasisko
varbūtību teoriju, viņas plaši izmanto mācību procesā. Vismaz - tā sākuma
stadijā. Tomēr pārmērīga šo piemēru
izmantošana, kā tas ir dažās
grāmatās, var radīt nepareizu
priekšstatu, ka varbūtību teorija ir galvenokārt spēļu teorijas daļa.
Mūsdienās, protams, tā nav.
Daudz
plašāks ir statistiskās varbūtības
definīcijas lietojums. Tā izmanto relatīvā biežuma jēdzienu. Par notikuma A relatīvo biežumu sauc novērojumu
skaita, kad A novērots, attiecību pret visu novērojumu skaitu. Relatīvo
biežumu parasti apzīmē ar burtu V.
Ja ir izdarīti n
novērojumi un notikums ir reģistrēts m
reizes, tad
![]() . (2.2)
. (2.2)
Ja,
izdarot preču kvalitātes pārbaudi, ir nejauši atlasīti 100 izstrādājumi un no
tiem 98 izrādījās derīgi, bet 2 - brāķis, tad derīgo izstrādājumu relatīvais
biežums ir
![]() .
.
Tālāk
statistiskā varbūtības definīcija balstās uz relatīvā biežuma stabilitāti. Ja
pārbaudītās preces piegādā viens un tas pats uzņēmums un savu ražošanas
tehnoloģiju nemaina, tad, pārbaudot citas analogas partijas, derīgo
izstrādājumu īpatsvars varētu būt 0,99,
0,97, 0,96, 1,00, 0,98,
bet nav domājams, ka tas būs 0,25 vai 0,57. Relatīvais biežums dažādās
vienos apstākļos izdarītās novērojumu sērijās svārstās ap kādu šiem apstākļiem
raksturīgu lielumu.
Skaitli,
ap kuru svārstās relatīvais biežums atsevišķās izmēģinājumu vai novērojumu
sērijās, sauc par notikuma A statistisko
varbūtību.
Ir novērots, ka šīs svarstības ir jo
mazākas, jo lielākas ir novērojumu sērijas. Tādēļ statistisko varbūtību definē
kā robežu:
![]()
![]() . (2.3)
. (2.3)
Pilnīgi
precīzu statistisko varbūtību nevar aprēķināt, jo nevar izdarīt bezgalīgi daudz
novērojumu. Bet vienmēr var noteikt tās tuvinātu vērtību. Tuvinājums būs
labāks, ja būs vairāk novērojumu.
Šīs
metodes izšķiroša priekšrocība ir tā, ka pirms varbūtības aprēķināšanas nav
jāzina notikuma iestāšanās iespēju skaits. Nav vajadzīgas aprioras zināšanas
par pētījuma objektu.
Citiem
vārdiem, ja klasiskā varbūtība ir jānosaka pirms novērojuma, tad statistiskā
varbūtība ir novērojuma vispārināšanas rezultāts.
Klasiskā
varbūtība asociējas ar deduktīvo, bet statistiskā - ar induktīvo izziņas procesu. Tādēļ tās ir dažādi
kopējā izziņas procesa aspekti. Ir meģināts izstrādāt varbūtības definīcijas,
kas sintezē šos aspektus. Piemēram, tā sauktā aksiomātiskā
varbūtības definīcija balstās uz abstraktu matemātisku kopu
jēdzieniem un šo kopu pretstatījumu. Tai ir nozīme teorētiskajā matemātikā.
Tādā ceļā veidotas definīcijas
sākotnējai izpratnei ir sarežģītas un tiešā veidā praksē grūti
izmantojamas.
Statistiskās
varbūtības plaši izmanto, piemēram, apdrošināšanas darbā. Ja runājam par dzīvības apdrošināšanu,
nepieciešamo apdrošināšanas maksu jeb prēmiju nosaka, vadoties no t.s. izdzīvošanas
jeb mirstības tabulām. Šajās tabulās, vadoties no statistikas datiem, ir
aprēķināta varbūtība katram noteikta dzimuma un vecuma iedzīvotājam nomirt nākošā mūža gadā. Jo šī varbūtība
lielāka, jo tiek prasīta lielāka apdrošināšanas prēmija. Izdzīvošanas tabulās
ietver arī vairākus citus interesantus rādītājus, piemēram, vidējo priekšā
stāvošo (sagaidāmo) gadu skaitu.
Vēl
ir lietderīgi iepazīties ar ģeometrisko
varbūtību jeb varbūtības ģeometrisko interpretāciju.
Šis
aspekts ir nepieciešams tad, ja pilna notikumu kopa sastāv no neierobežoti
daudziem elementāriem notikumiem. Tad katra atsevišķa elementāra notikuma
varbūtība ir tik niecīga, ka to kā robežu var uzlūkot par nulli. Tad
interesējamies par kādas notikumu apakškopas varbūtību, kuru kaut kādā veidā
var izdalīt no pilnās notikumu kopas.
Pilno
notikumu kopu attēlojam ar vienu ģeometrisku figūru, bet interesējošo jeb
labvēlīgo kopu - ar citu pirmajā figūrā ietvertu figūru. Tad atsevišķus
elementāros notikumus var iedomāties kā punktus, kuri visi nonāk lielajā
figūrā, bet daļa no tiem nejauši arī mazajā. Ja
punktu sadalījums lielās figūras ietvaros ir vienmērīgs, tad varbūtību,
ka gadījuma notikums (punkts) nonāks izdalītajā kopā (mazajā figūrā), var aprēķināt
kā šo figūru laukuma attiecību:
![]() . (2.4)
. (2.4)
Figūras
nevar interpretēt kā laukumus ģeogrāfiskā kartē!
Reālu
procesu, kas atbilst ģeometriskās varbūtības saturam, var iedomāties šādi. Ir
jāizgatavo medikaments (zāles) tablešu veidā, pie kam katra tablete satur
1/1000 grama darbīgās vielas. Lai tabletes būtu ērti lietojamas, pieņemam, ka
katras tabletes svaram jābūt 1 gr. lielam.
Iesvērt
1/1000 gr. atsevišķi katrai tabletei praktiski nav iespējams. Tādēļ ņem 1 gr.
darbīgās vielas un 1 kg nekaitīgas, neitrālas balastvielas un tās maksimāli
rūpīgi sajauc (parasti šķīduma veidā, jo
pulverveidā tas grūti iespējams). Pēc tam ņem 1 gr. maisījuma un samērā
droši cer, ka tas saturēs ap 1/1000 gr. darbīgās vielas. (1kg masa šeit saskaņā ar formulu ir S, bet 1 gr. darbīgās vielas masa ![]() ). Saskaitīt un aprēķināt katras molekulas varbūtību nonākt
kārtējā tabletē nav iespējams.
). Saskaitīt un aprēķināt katras molekulas varbūtību nonākt
kārtējā tabletē nav iespējams.
2.1.3. Varbūtības galvenās īpašības
1. Droši
sagaidāma notikuma varbūtība ir viens.
Ja labvēlīgo iespēju skaits sakrīt ar
visu iespēju skaitu, tad M = N un
no klasiskās varbūtības definīcijas izriet, ka viņu dalījums ir viens.
2. Neiespējama
notikuma varbūtība ir nulle.
Ja izdarot novērojumu, kādam notikumam
nav labvēlīgu iespēju, tad M = 0 un no formulas (2.1) redzams, ka
varbūtība ir nulle.
3. Gadījumnotikuma
varbūtība ir skaitlis, lielāks par nulli un mazāks par vienu.
Ja notikums ir gadījumnotikums, tad
tam labvēlīgo iespēju skaits ir mazāks par visu iespēju skaitu, tātad M < N, no kā seko, ka
0 < P(A) < 1. (2.5)
Šīs īpašības izriet arī no varbūtības
statistiskās definīcijas. Ja statistiskā
kopa sastāv vismaz no divām daļām, tad katras daļas relatīvais biežums
ir mazāks par vienu. Daži autori šīs īpašības uzlūko par aksiomām, citi tās
pierāda, izejot no varbūtības definīcijas.
4. Praktiskajā interpretācijā varbūtības var izteikt arī
procentos. Tam nolūkam varbūtība viena daļās ir jāpareizinā ar simtu. Līdz ar
to gadījuma notikuma varbūtība vienmēr ir lielāka par 0 un mazāka par 100%. Matemātikā varbūtību izsaka viena daļās. Ar
viena daļās izteiktu varbūtību daudz ērtāk izpildīt dažādas matemātiskas
darbības.
5. Praktiskā darbā notikumu uzlūko par
droši sagaidāmu, ja tā iestāšanās varbūtība ir tuva vienam. Notikumu uzlūko par
praktiski neiespējamu, ja tā varbūtība ir tuva nullei. Kādas varbūtības dod
iespēju izdarīt šādus secinājumus, ir atkarīgs no tā, cik nevēlamas vai pat
bīstamas ir sekas, ja notikums ar kuru rēķināmies kā ar drošu, tomēr nenotiek
un otrādi.
Piemēram, ja students cer nokārtot
eksāmenu ar varbūtību 0,9, viņš uz eksāmenu droši vien ieradīsies. Bet, ja tas
pats students lidostā saņems brīdinājumu, ka varbūtība sekmīgam reisam ir 0,999
(tikai katrā tūkstošajā reisā lidmašīna nogāžas), viņš droši vien atteiksies no
lidojuma.
Mācību literatūrā un virknē praktisku
uzdevumu par droši sagaidāmu uzlūko notikumu, ja tā notikšanas varbūtība ir
0,95 vai 0,99. Atbilstoši par
neiespējamu uzlūko notikumu, kura notikšanas varbūtība ir 0,05 vai 0,01.
Tehnikā šīs varbūtības parasti vajadzīgas augstākas, vismaz 0,999, resp. 0,001.
Pārbaudot statistiskās
hipotēzes, varbūtību, ar kuru kādu apgalvojumu var pieņemt par
praktiski neiespējamu, sauc arī par nozīmības līmeni. Parasti lieto 0,1; 0,05;
0,01 nozīmības līmeni. No šabloniskas pieejas vajadzētu izvairīties.
2.2. Vienkāršākās darbības ar varbūtībām
Darbības
ar varbūtībām izdara tad, ja kādu notikumu varbūtības ir zināmas, bet
jāaprēķina kādu citu notikumu varbūtības, kuri ar pirmajiem ir saistīti.
Vienkāršākajos uzdevumos ir dotas elementāro notikumu varbūtības, bet jāaprēķina salikto jeb neelementāro notikumu varbūtības. Tādus
uzdevumus atrisina, izdarot vienkāršas darbības ar varbūtībām. Lai atrisinātu
sarežģītākus uzdevumus, parasti vajag sastādīt vienādojumus vai to sistēmas,
kurās ietilpst varbūtības.
2.2.1. Nesavienojamu notikumu varbūtību saskaitīšana
Varbūtību saskaitīšanu lieto tad, ja ir
jāaprēķina gadījuma notikumu apvienojuma jeb loģiskās summas varbūtība. Sākumā
aplūkosim uzdevumus, kur ir runa tikai par
diviem savstarpēji nesavienojamiem gadījuma notikumiem.
Lai
uzdevumi būtu maksimāli vienkārši, izmantosim piemēru no klasiskās teorijas
resp. spēļu situācijām.
Piemēram,
vienojas, ka spēles situācijā uzvar tad, ja, metot spēļu kauliņu, uzkrīt
skaitlis 6 vai 5. Jāaprēķina varbūtība uzvarēt kārtējā mēģinājumā.
Analīze.
Pareizam spēļu kauliņam ir 6 skaldnes, kurām visām pēc metiena ir vienāda
iespēja palikt virspusē, kur nolasa skaitli. Tā kā viena no skaitļiem 1 līdz 6
uzkrišana ir droši sagaidāms notikums, kura varbūtība ir 1, tad šī varbūtība 1
ir jāsadala sešās līdzīgās daļās, iegūstot varbūtību, ar kādu var sagaidīt
vēlamā skaitļa uzkrišanu.
Līdz ar to
![]() .
.
Tās
ir elementāro notikumu varbūtības, kuras nosaka pirms mēģinājuma.
Skaitļa
6 vai 5 uzkrišana, kas ved pie uzvaras, ir neelemantārs notikums, kurš veidojas
no diviem elementāriem notikumiem. Tā ka vienā metienā var uzkrist tikai viens skaitlis, abi
elementārie notikumi ir nesavienojami.
Par
divu gadījuma notikumu A un B apvienojumu sauc notikumu C,
kurš jāsaprot kā A vai B, vai A un B kopēja notikšana (pēdējā piemērā nav
iespējama).
Notikumu
apvienojumu matemātiskā apzīmē šādi
![]() ,
,
kur U -
apvienošanas zīme, ko lasa ar vārdu ''vai''.
Ja A un B ir nesavienojami, tad to kopējas
notikšanas varbūtība ir nulle. Līdz ar to varbūtību, ka viena izmēģinājuma
rezultātā notiks viens no šiem notikumiem, aprēķina kā abu notikumu varbūtību
summu:
![]() . (2.6)
. (2.6)
Piemērā
![]() .
.
Brīdinājums!
Šo formulu nevar lietot, ja gadījumnotikumi ir savstarpēji savienojami.
Piemēram, vienojas, ka metot spēļu kauliņu uzvar tad, ja uzkrīt 6 vai
pārskaitlis. Uzkrītot 6, ir uzkritis arī pāskaitlis. Tādēļ šeit pietiek rēķināt
vienīgi pārskaitļa uzkrišanas varbūtību ![]() . Pieskaitot vēl skaitļa 6 uzkrišanas varbūtību, pieļausim
dublēšanu, iegūstot kļūdainu rezultātu.
. Pieskaitot vēl skaitļa 6 uzkrišanas varbūtību, pieļausim
dublēšanu, iegūstot kļūdainu rezultātu.
Varbūtību
saskaitīšanas teorēmu var attiecināt uz vairāk nekā diviem nesavienojamiem
gadījumnotikumiem:
![]() . (2.7)
. (2.7)
No
varbūtību saskaitīšanas teorēmas izriet, ka pilnu kopu veidojošu gadījuma
notikumu varbūtību summa ir viens
![]() , (2.8)
, (2.8)
ja
![]() - pilna notikuma
kopa. Šo īpašību bieži izmanto aprēķinu loģiski aritmetiskai kontrolei.
Aksiomātiskajā varbūtību teorijā šo apgalvojumu pieņem kā aksiomu.
- pilna notikuma
kopa. Šo īpašību bieži izmanto aprēķinu loģiski aritmetiskai kontrolei.
Aksiomātiskajā varbūtību teorijā šo apgalvojumu pieņem kā aksiomu.
Iepriekšējās
formulas sekas ir apgalvojums, ka divu pretēju
notikumu varbūtību summa ir viens
![]() , (2.9)
, (2.9)
jo tie veido pilnu kopu.
Pretēju
notikumu varbūtības bieži apzīmē ar p un q.
Tādējādi
p + q = 1. (2.10)
Ja viena pretēja notikuma varbūtība ir
zināma, otru viegli aprēķināt pēc šīs sakarības.
2.2.2. Neatkarīgu notikumu varbūtību reizināšana
Varbūtību reizināšanu lieto, ja ir
jāaprēķina gadījuma notikumu šķēluma jeb kopējas notikšanas varbūtība.
Vienkāršākajā gadījumā šiem notikumiem jābūt savstarpēji neatkarīgiem.
Divus
gadījuma notikumus sauc par savstarpēji
neatkarīgiem, ja viena notikuma iestāšanās varbūtība nav atkarīga no
tā, vai otrs notikums jau noticis vai nē ( un arī otrādi).
Par
divu gadījuma notikumu A un B šķēlumu jeb reizinājumu sauc notikumu D,
kurš jāsaprot kā A un B kopēja notikšana. Varbūtību teorijā
notikumu šķēlumu apzīmē šādi ![]() , kur
, kur ![]() šķēluma (loģiskā
reizinājuma) zīme. To lasa kā ''un''.
šķēluma (loģiskā
reizinājuma) zīme. To lasa kā ''un''.
Varbūtību
reizināšanu pamato šāda teorēma.
Divu
neatkarīgu gadījumnotikumu kopējas notikšanas
varbūtība ir vienlīdzīga abu šo notikumu varbūtību reizinājumam:
![]() . (2.11)
. (2.11)
Varbūtību
reizināšanas teorēmu var attiecināt uz vairāk nekā diviem neatkarīgiem gadījuma
notikumiem
![]() . (2.12)
. (2.12)
Piemērs.
1.
Automātiskajā līnijā saistīti divi darbgaldi.
Spriežot pēc iepriekšējiem novērojumiem, varbūtība, ka katrs atsevišķi
ņemts darbgalds visu maiņu būs darba kārtībā, ir 0,9. Ar kādu varbūtību var
sagaidīt, ka visa līnija maiņu nostrādās bez traucējumiem?
Atbildi
atrod, varbūtības sareizinot
![]() .
.
Nedaudz
sarezģītāku uzdevumu atrisinājuma pareizību bieži var pārbaudīt, izrēķinot visu
pilnu kopu veidojošo notikumu varbūtības un atrodot šo varbūtību summu, kurai
jābūt viens.
Piemērs.
Cehā
ir divi viena tipa darbgaldi. Varbūtība, ka katrs no tiem visu maiņu būs
kārtībā, ir 0,9. Atrast varbūtību, ka vismaz viens no viņiem būs kārtībā.
Intuitīvi
nojaušam, ka meklētai varbūtībai jābūt lielākai nekā 0,9 ,
jo cerība, ka no diviem darbgaldiem viens būs kārtībā, ir lielāka nekā
tad, ja ir tikai viens darbgalds. Tas var pamudināt lietot varbūtību
saskaitīšanu
0,9 + 0,9 = 1,8.
Iegūtais
rezultāts ir nepārprotams brīdinājums, ka pieļāvām kļūdu. Nekāda notikuma
(elementāra vai nelementāra) varbūtība nevar būt lielāka par vienu.
Kļūda
radās tajā apstāklī, ka nepamatoti lietojām varbūtību saskaitīšanu. Var
saskaitīt tikai to notikumu varbūtības, kuri var rasties viena novērojuma vai
mēģinājuma rezultātā un ir savstarpēji neatkarīgi. Piemērā, turpretī, ir runa
par diviem patstāvīgi lietojamiem darbgaldiem, no kuriem katrs var atrasties
divos stāvokļos: darba kārtībā vai bojāts.
Jāatzīmē,
ka nepareizi lietojot varbūtību saskaitīšanu, ne vienmēr iegūst skaitli lielāku
par 1, līdz ar to pamanot aprēķinu nepareizību. Tādēļ šaubu gadījumos ir
jāsastāda pilns vienīgi iespējamo neelementāro notikumu saraksts, jāatrod visu to varbūtības un, šīs varbūtības
saskaitot, jāiegūst skaitlis 1, jo viena no vienīgi iespējamiem notikumiem
iestāšanās ir drošs notikums.
Pēc
tam var novērtēt, kuri no pilna notikumu saraksta atbilst uzdevuma prasībām.
Mūsu
piemērā pilnu neelementāro notikumu kopu veido šādi notikumi:
1.
abi darbgaldi kārtībā, varbūtība 0,9
× 0,9 = 0,81;
2.
pirmais darbgalds kārtībā, otrs bojāts, varbūtība 0,9 × 0,1 = 0,09;
3.
otrais darbgalds kārtībā, pirmais bojāts, varbūtība 0,1 × 0,9 = 0,09;
4.
abi darbgaldi bojāti, varbūtība 0,1
× 0,1 = 0,01
__________________________
varbūtību summa 1,00
Uzdevuma
nosacījumiem atbilst pirmie trīs notikumi, tadēļ varbūtība, ka kaut vai viens
darbgalds būs kārtībā, ir šāda: 0,81 +0,09 + 0,09 = 0,99.
Iepriekšējo uzdevumu var atrisināt
atrāk, zinot šādu vismaz viena
notikuma notikšanas varbūtības teorēmu.
Varbūtību, ka notiks vismaz viens no
notikumiem ![]() , kuri ir savstarpēji
neatkarīgi, var aprēķināt, atņemot no skaitļa viens pretējo notikumu
, kuri ir savstarpēji
neatkarīgi, var aprēķināt, atņemot no skaitļa viens pretējo notikumu ![]() varbūtību
reizinājumu.
varbūtību
reizinājumu.
Parasti to pieraksta saīsināti:
![]() . (2.13)
. (2.13)
Iepriekšējā piemēra atrisinājums būs
![]() ,
,
kas saskan ar iepriekšējo.
Sarežģītāku
uzdevumu risināšanai darbības ar varbūtībām ir dažādi jākombinē. Uzdevuma
risināšanas gaitā labi palīdz grafiska analīze: Eilera-Venna diagrammas,
virzīto grafu attēls u.c. Šaubu gadījumos vienmēr jācenšas sastādīt pilnu
notikumu kopas un jāpanāk, lai šo notikumu varbūtību summa būtu viens.
2.2.3. Varbūtību vienādojumi un vienādojumu sistēmas.
Ja
viena elementāra notikuma varbūtība nav zināma, bet citu elementāru notikumu
varbūtības ir zināmas, turklāt, ir zināma kāda neelementāra notikuma varbūtība,
kurš jāsaprot kā minēto elementāro notikumu apvienojums, šķēlums vai citāda
sintēze, tad nezināmo elementārā notikuma varbūtību bieži var aprēķināt,
sastādot un atrisinot varbūtību vienādojumu.
Piemērs.
Elektronisko
aparātu samontē no trim samērā autonomiem blokiem. Pirmos divus blokus montāžas
cehā pirms izmantošanas pārbauda īpašos stendos. Ja pirmais bloks stenda
pārbaudē ir atzīts par derīgu, tad tas ir derīgs arī izgatavojamā aparātā ar
varbūtību 0,99. Ja stenda pārbaudē otrais bloks ir atzīts par derīgu, tas ir
derīgs arī izgatavojamā aparātā ar varbūtību 0,98. Trešā bloka autonomai
pārbaudei cehā stenda nav. To iemontē aparātā, paļaujoties uz piegādājošās
rūpnīcas pārbaudes rezultātiem. Pēc tam pārbauda izgatavoto aparātu kopumā.
Izrādās ka 90% no tiem uzreiz darbojas normāli. Vienkāršības dēļ pieņem, ka
aparāts darbojas normāli vienmēr un tikai tad, ja pareizi darbojas visi trīs tā bloki.
Uzdevums:
Atrast varbūtību, ka kārtējais no iesaiņojuma
izņemtais trešais bloks būs derīgs. (To var interpretēt arī kā derīgo
bloku īpatsvaru).
Analīze un atrisinājums.
Apzīmējam ar ![]() varbūtību, ka pirmais
bloks ir derīgs. Piemērā
varbūtību, ka pirmais
bloks ir derīgs. Piemērā
![]() .
.
Ar ![]() apzīmējam varbūtību,
ka otrais bloks ir derīgs,
apzīmējam varbūtību,
ka otrais bloks ir derīgs, ![]() .
.
Ar
![]() apzīmējam varbūtību,
ka trešais bloks ir derīgs. Tā mums ir jāaprēķina.
apzīmējam varbūtību,
ka trešais bloks ir derīgs. Tā mums ir jāaprēķina.
Ar
P (lielais) apzīmējam varbūtību, ka derīgs aparāts kopumā.
Minētos
lielumus, kā izriet no uzdevuma satura, saista vienādība:
![]() .
.
Izdarot ievietojumus, iegūstam, ka
![]() .
.
No tā seko, ka
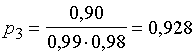 .
.
Atbilde.
Varbūtība, ka kārtējais no iesaiņojuna paņemtais trešais bloks būs
derīgs (bez papildus pārbaudes) ir 0,928. Citiem vārdiem, piegādātajā partijā
ir bijuši 92,8% derīgu bloku.
Citos
uzdevumos sakarības var būt sarežģitākas. Tad sarežģitāks būs arī varbūtību
vienādojums.
Ja
ir nezināmas vairāku elementāru notikumu
varbūtības, tad tās var aprēķināt, ja izdodas sastādīt un atrisināt attiecīgu
varbūtību vienādojumu sistēmu.
2.3.
Darbības ar savstarpēji atkarīgu notikumu varbūtībām
2.3.1.
Nosacītā varbūtība
Ja
viena notikuma varbūtība ir atkarīga no tā, vai otrs notikums ir noticis vai
nē, tad šie notikumi ir savstarpēji atkarīgi.
Ja
notikumi A un B ir savstarpēji atkarīgi, tad par nosacīto varbūtību ![]() sauc notikuma B
varbūtību, pieņemot, ka A jau noticis.
sauc notikuma B
varbūtību, pieņemot, ka A jau noticis.
Saistot
varbūtību jēdzienus ar izlases metodi, var teikt, ka nenosacītās varbūtības
asociējas ar atkārtoto, bet nosacītās - ar neatkārtoto izlasi.
Piemērs.
Māņticīgs students eksamenā baidās no 13. biļetes. Vai viņam ir lielāka
varbūtība to izvilkt, ņemot biļeti pirmajam, vai pēdējam? Pieņemam, ka uz
eksāmenu ir ieradušies 20 studenti un sagatavotas izlozei 30 biļetes.
Analīze.
Ja students ņem biļeti pirmais, tad ''nevēlama'' notikuma varbūtība ir
![]() .
.
Ja
viņš ņem biļeti pēdējais, tad varbūtība ir atkarīga no tā, vai šo biļeti
iepriekš ir paņēmis kāds cits students vai nē. Ja to ir paņēmis kāds cits, tad
varbūtība kļūst nulle. Bet, ja neviens cits to nav paņēmis, tad nelabvēlīgo
iespēju skaits M=1 nemainās, bet visu iespēju skaits N
no 30 samazinās līdz 30 - 19 = 11. Tātad varbūtība ir ![]() un tā ir daudz
lielāka, nekā ņemot biļeti sākumā.
un tā ir daudz
lielāka, nekā ņemot biļeti sākumā.
2.3.2. Nosacīto varbūtību reizināšana
Vienkāršākajā
gadījumā ir runa par diviem atkarīgiem
notikumiem A un B, kuru varbūtības P(A) un ![]() ir dotas. Ir
jāatrod varbūtība, ka abi notikumi
notiks kopā ( vienlaikus, viens pēc otra).
ir dotas. Ir
jāatrod varbūtība, ka abi notikumi
notiks kopā ( vienlaikus, viens pēc otra).
Izmanto
šādu teorēmu.
Divu
atkarīgu notikumu kopējas notikšanas
varbūtību aprēķina, reizinot viena notikuma parasto varbūtību ar
otra notikuma nosacīto varbūtību
![]() . (2.14)
. (2.14)
Ja
uzdevumā nav īpaši atrunāts, pieņem, ka notikumu vietas var savstarpēji mainīt.
Tā kā
![]() . (2.15)
. (2.15)
Piemērs. Traukā
ir 50 loterijas biļetes, no kurām 25 atzīmēts laimests. Kāda varbūtība
izvilkt divas laimējošas biļetes pēc kārtas?
Atrisinājums. Pirmajā meģinājumā varbūtība ir ![]() .
.
Otrajā mēģinājumā 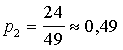 .
.
Abos mēģinājumos ![]() .
.
Teorēmu var attiecināt uz vairāk nekā
diviem atkarīgiem notikumiem. Tad trešā notikuma nosacīto varbūtību nosaka,
ņemot vērā, ka notikuši divi pirmie u.t.t.
2.3.3. Savienojamu notikumu varbūtību saskaitīšana
Divus
gadījumnotikumus sauc par savienojamiem,
ja viena notikšana neizslēdz otra notikšanu tajā pat izmēģinājumā.
Piemērs.
Izlases veidā pārbaudot izgatavoto magnetofonu partiju, konstatēts, ka I šķiras
standarta normām neatbilst 20% sakarā ar šaurāku atskaņojamo frekvenču joslu un 10% sakarā ar pazeminātu
stereokanālu selektivitāti. Vienkāršības dēļ citus iespējamos defektu
veidus neņemam vērā. Kāda varbūtība,
pērkot vienu aparātu no šīs partijas, ka tas nebūs I šķiras?
Uzdevuma situāciju Eilera - Venna
diagrammā var ilustrēt šādi. (2.1. attēlā)
![]()
![]()
![]()
![]() 2.1.
attēls. Savienojamu gadījumnotikumu
2.1.
attēls. Savienojamu gadījumnotikumu
1 def.![]()
![]()
grafiska ilustrācija.
Tā
kā vienam aparātam vienlaikus var būt abi defekti, varbūtību vienkārša
saskaitīšana dos nepamatoti palielinātu defektīvo aparātu varbūtību.
Šeit
jālieto teorēma, kuras saturs ir skaidrs no diagrammas.
Varbūtība,
ka notiks viens no savstarpēji savienojamiem notikumiem, ir vienlīdzīga šo
notikumu varbūtību summai, no kuras atskaitīta
abu notikumu kopīgas iestāšanās varbūtība, resp., varbūtību reizinājums.
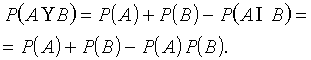 (2.16)
(2.16)
Piemērā varbūtība nopirkt zemākas
šķiras aparātu ir
![]() .
.
Varbūtība nopirkt I šķiras aparātu šādā situācijā ir minētās
varbūtības papildinājums līdz vienam, kā tas redzams no 2.2. attēla.
 1 - 0,28
= 0,72.
1 - 0,28
= 0,72.


2 def. 1 def.
2.2.
attēls. Pretēja gadījumnotikuma
grafiska ilustrācija.
Atliek
salīdzināt formulas (2.16) un (2.6), jo
viņas var radīt pārpratumus. To kreisās puses ir pierakstītas vienādas, bet
labās atšķirīgas. Atšķirību cēlonis ir tas, ka formulas (2.6) lietošanu ierobežo papildus nosacījums,
ka abi notikumi ir savstarpēji nesavienojami. Eilera - Venna diagrammā apļi nešķeļās.
Tādēļ ![]() un
un
![]() .
.
Formulā (2.16) šī
ierobežojuma nav. Tādēļ tajā ietver locekli ![]() un formula ir
universālāka.
un formula ir
universālāka.
2.4.
Vidējās un pilnās varbūtības formulas. Beijesa formula
2.4.1.
Vidējā un pilnā varbūtība
Šo uzdevumu nostādni vislabāk ilustrēt ar piemēriem.
Uzdevums.
Viena
veida detaļas izgatavo divi strādnieki un liek kopējā kastē. No iepriekšējās
hronometrāžas ir zināms, ka pirmais strādnieks izgatavo 60%, bet otrais 40% no
kopējā skaita. Bez tam iepriekšējā pārbaude ir parādījusi, ka derīgo detaļu
īpatsvars pirmajam strādniekam ir 90%, bet otrajam 95%. Aprēķināt, kāda
varbūtība, ka kārtējā detaļa, ko nejauši ņemsim no kastes, būs derīga.
Analīze un
atrisinājums.
Acīmredzot,
varbūtība nevar būt zemāka par 0,9 un augstāka par 0,95. Šīs robežvērtības
varbūtība iegūtu tad, ja strādātu tikai
viens strādnieks: vai nu paviršākais vai rūpīgākais. Tā kā strādā abi, tad
meklētai varbūtībai jābūt divu robežvērtību vidējam lielumam, kur par svariem
ņemam izgatavoto detaļu īpatsvaru. Izsverot viena daļās - 0,6 un 0,4. Tātad
intuitīvs risinājums ir svērtais aritmētiskais vidējais.
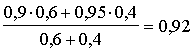 .
.
Varbūtību
teorijā vajadzīgo varbūtību aprēķina, lietojot pilnās
varbūtības formulu:
![]() . (2.17)
. (2.17)
Piemērā
varbūtība, ka nejauši ņemto detaļu būs izgatavojis pirmais strādnieks, ir ![]() , ka otrais strādnieks -
, ka otrais strādnieks -
![]() . Nosacītā varbūtība,
ka detaļa būs derīga, ja to izgatavojis
pirmais strādnieks
. Nosacītā varbūtība,
ka detaļa būs derīga, ja to izgatavojis
pirmais strādnieks ![]() , ja izgatavojis
otrais strādnieks
, ja izgatavojis
otrais strādnieks ![]() .
.
Ievietojot
formulā, iegūstam
![]() .
.
Pilnās varbūtības formula neparedz
dalīšanu ar statistisko svaru summu
![]()
kā to darījām intuitīvajos aprēķinos,
jo tā vienmēr ir viens. Varbūtību summa ir viens, tādēļ, ka ![]() un
un ![]() veido pilnu notikumu
kopu.
veido pilnu notikumu
kopu.
Darbības
ar nosacītajām varbūtībām labi var ilustrēt ar virzītu grafu attēlu. Šāds
attēls palīdz arī atrisināt samērā
grūtākus uzdevumus.
Parādīsim
pilnās varbūtības formulas grafisku ilustrāciju, izmantojot iepriekšējo piemēru
(2.3. attēls).
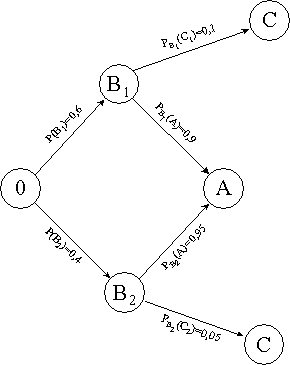
2.3.attēls.
Pilnās varbūtības vienkāršākā gadījuma grafiska ilustrācija.
Pieņemam,
ka no virsotnes ''O'' (nulle) virsotnes ''A'' virzienā plūst kāda plūsma
(šķidrums, elektriskā strāva, klienti masu apkalpošanas teorijā). Izpētām, kādu
ceļu veic šī plūsma.
No
virsotnes 0
plūsma sadalās divās daļās: uz virsotni
![]() un
un ![]() . Piemērā detaļas
sagatavi paņem pirmais
strādnieks (plūsma
. Piemērā detaļas
sagatavi paņem pirmais
strādnieks (plūsma ![]() ) vai otrais
strādnieks
) vai otrais
strādnieks ![]() . Abas šīs plūsmas
kopā aptver visu plūsmu. Attiecīgo varbūtību summa ir viens.
. Abas šīs plūsmas
kopā aptver visu plūsmu. Attiecīgo varbūtību summa ir viens.
Virsotnēs ![]() un
un ![]() plūsma atkal dalās
divās daļās : strādnieka izgatavotā detaļa ir derīga - uz virsotni A
vai brāķis - uz virsotni C (var zimēt arī vienu virsotni C)
Abi plūsmas zari no katras virsotnes B atkal aptver visu plūsmu. Nosacīto
varbūtību summa ir viens.
plūsma atkal dalās
divās daļās : strādnieka izgatavotā detaļa ir derīga - uz virsotni A
vai brāķis - uz virsotni C (var zimēt arī vienu virsotni C)
Abi plūsmas zari no katras virsotnes B atkal aptver visu plūsmu. Nosacīto
varbūtību summa ir viens.
Mūs
interesē, kāda daļa no visas plūsmas, kas iziet no virsotnes 0, nonāk virsotnē A.
Varbūtības šajā gadījumā var interpretēt kā plūsmas intensitāti katrā ceļa
posmā.
Ja
grafu attēlā ir fiksēti visi ceļi, kas ved no 0 uz A, un no katras virsotnes aizejošo ceļu
plūsmas intensitātes blīvumu summa ir viens, tad minēto un līdzīgus uzdevumus
atrisina, izmantojot šādu mnemonisku
likumu.
Lai
atrastu plūsmas daļu, kas nonāk no virsotnes ''0'' virsotnē ''A'' ,
secīgi ejamo ceļu kustības blīvumi (varbūtības) ir jāsareizina, bet
paralēli iespējamo ceļu kustību blīvumi (varbūtības) jāsaskaita.
Pierakstot
šo likumu algebriski, iepriekšējam grafu attēlam iegūstam
pilnās varbūtības formulu. (2.18)
Izmantojot
analogu zīmējumu ar brīvi izvēlētu skaitu paralēli iespējamo ceļu, iegūstam pilnās varbūtības vispārējo formulu (skat 2.4. attēlu).
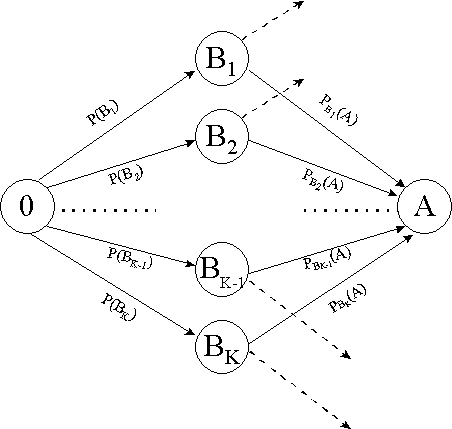
2.4.attēls.
Pilnās varbūtības vispārējā gadījuma grafiska ilustrācija.
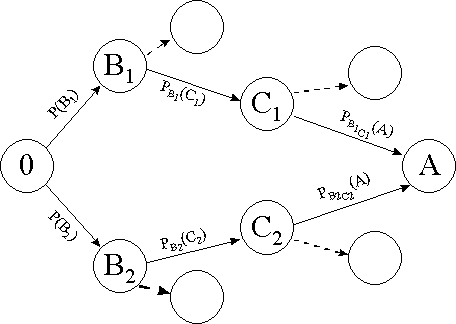
2.5.attēls. Pilnās varbūtības grafiska
ilustrācija, ja gadījumnotikumu
ķēde ir garāka.
![]() (2.18)
(2.18)
Līdzīgi var risināt arī uzdevumus,
kuru grafu attēlā ir vairāk nekā divi secīgi ceļa posmi. Piemēram (skat 2.5.
attēlu).
Pilnās
varbūtības formulas labajā pusē šajā gadījumā būs divi saskaitāmie (atbilstoši
paralēlo ceļu skaitam), bet katru no tiem aprēķina kā trīs skaitļu reizinājumu.
2.4.2. Beijesa formula
Beijesa
formulas lietošanu parādīsim ar piemēru.
Piemērs. Iepriekšējie novērojumi rāda,
ka ražošanas iecirknis izgatavo 90% standarta un 10% nestandarta detaļu.
Detaļas pārbauda tehniskā kontrole. Citi novērojumi rādīja, ka 95% standarta
detaļu atzīst par derīgām, bet 5% kļūdas dēļ izbrāķē. Savukārt, pārbaudot
nestandarta detaļas, 90% gadījumu brāķi atklāj, bet 10% gadījumu to nepamana.
Uzdevums
atrast varbūtību, ka detaļa, kas tehniskajā kontrolē jau ir atzīta par
atbilstošu standartam, patiešām būs derīga.
Analīze.
Par
notikumu A pieņemsim faktu, ka detaļu tehniskā kontrole atzīst par
derīgu. Tas var iestāties tad, ja iepriekš noticis notikums ![]() (izgatavota standarta
detaļa) vai
(izgatavota standarta
detaļa) vai ![]() (izgatavota
nestandarta detaļa). Lai situācija būtu pilnīga, ar C
apzīmēsim detaļas izbrāķēšanu, kaut gan uzdevuma atrisināšanai tas nav
nepieciešams (skat. 2.6. attēlu).
(izgatavota
nestandarta detaļa). Lai situācija būtu pilnīga, ar C
apzīmēsim detaļas izbrāķēšanu, kaut gan uzdevuma atrisināšanai tas nav
nepieciešams (skat. 2.6. attēlu).
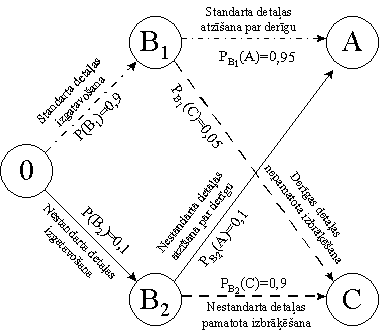
2.6.attēls.
Beijesa formulas grafiska ilustrācija.
Notikuma
A
varbūtību aprēķina pēc pilnās varbūtības formulas. Tā ir varbūtība, ka kārtējo
detaļu tehniskā kontrole atzīs par derīgu:
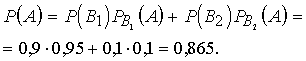
Šo varbūtību var raksturot kā plūsmas
daļu, kura nonāk no virsotnes O virsotnē A
pa abiem iespējamiem ceļiem ![]() un
un ![]() . Bet uzdevuma
nosacījumiem atbilst tikai ceļš
. Bet uzdevuma
nosacījumiem atbilst tikai ceļš ![]() . Plūsmas daļu, kura nonāk virsotnē A
pa šo ceļu, raksturo pilnās varbūtības pirmais saskaitāmais
. Plūsmas daļu, kura nonāk virsotnē A
pa šo ceļu, raksturo pilnās varbūtības pirmais saskaitāmais
![]() .
.
Saskaņā
ar uzdevuma nosacījumiem detaļa jau ir nonākusi virsotnē A,
bet nav zināms, pa kuru ceļu. Varbūtību, ka tas ir bijis pirmais ceļš,
raksturos plūsmu intensitātes attiecība pirmajā ceļā un visā kontūrā OA (t.i. pa abiem ceļiem).
Tātad 0,855:0,865 = 0,988.
Atrasto
varbūtību sauc par hipotēzes varbūtību
tādēļ, ka reālais plūsmas ceļš ir OBA, bet mēs domās pieņemam, ka notikums A
jau ir noticis (detaļa ir nonākusi virsotnē A) un novērtējam atpakaļvirzienā, par
kuru no ceļiem tas varētu būt noticis.
Šādus
uzdevumus vispārina Beijesa formula.
Gadījumam, ja pilno varbūtību veido divi saskaitāmie (grafā ir divi ceļi), Beijesa formula ir šāda:
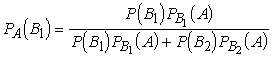 , (2.19)
, (2.19)
kur saucējā ir pilnās varbūtības
formulas labā puse.
Piemērā:
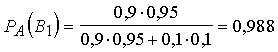 .
.
Varbūtība,
ka tehniskajā kontrolē pārbaudītā un atzītā detaļa patiešām būs derīga, ir
0,988.
Beijesa
formulu var izrisināt matemātiski, izdarot virkni pārveidojumu un substitūciju
saskaņā ar teorēmām par darbībām ar varbūtībām.
Analogi
var izrēķināt, kāda būs varbūtība, ka detaļa, ko tehniskā kontrole atzinusi par
derīgu, īstenībā būs brāķis.
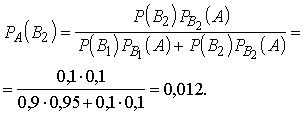
Abu
varbūtību summa ir viens.
Ja
pilno varbūtību veido vairāk kā divi saskaitāmie, grafiskajā attēlā ir vairāk
kā divi ''ceļi''. Tad iegūstam Beijesa formulu vispārīgā
veidā.
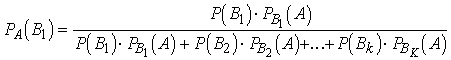 .
.
Tā
raksturo varbūtību, ka interesējošā objekta vienība, kura jau ir nonākusi
virsotnē A, tur ir nonākusi pa pirmo ceļu. Pirmā ceļa vietā var ņemt
jebkuru citu; tad ![]() jāaizstāj ar
jāaizstāj ar ![]() .
.
Situāciju
var sarežģīt vēl tālāk, interesējoties par varbūtību, ka interesējošā vienība
ir nonākusi virsotnē A pa vienu no diviem vai vairākiem
fiksētiem ceļiem no lielāka skaita iespējamo.
Tad
arī Beijesa formulas skaitītājā būs divi vai vairāki saskaitāmie, bet saucējā
joprojām paliks pilnā varbūtība.
Vēl
iespējams, ka ceļos ir nevien viens, bet divi vai vairāki krustpunkti
(virsotnes). Tad vajadzīgo formulu visvieglāk izveidot, iepriekš izgatavojot
un izanalīzējot grafisko attēlu.
2.5. Atkārtoti novērojumi. Bernulli formula un Ņutona
binoms
Par
atkārtotu novērojumu vai izmēģinājumu
sauc vienas un tās pašas apstākļu kopas atkārtotu radīšanu, kuras rezultātā
notikums A var notikt vai nenotikt.
Ja
notikums A ir gadījumnotikums, tad rodas raksturīgs uzdevums
aprēķināt, kāda ir varbūtība, ka novērojumu atkārtojot n reizes, notikums A
iestāties tieši m reizes.
No tā seko, ka notikums A n-m reizes nenotiks. Pieņem, ka
notikuma A varbūtība visos novērojumos ir vienāda, un to apzīmē ar p.
Jāizšķir divas uzdevuma nostādnes.
1. Mūs interesē varbūtība, ka notikums
A
notiks m reizes iepriekš fiksētā secībā, piemēram, visas m reizes novērojumu
sērijas sākumā.
Tādu varbūtību var aprēķināt ar
elementāru varbūtību reizināšanu, to
saīsinot ar kāpināšanas darbību palīdzību. Proti
![]() .
.
2. Biežāk interesē varbūtība, ka
notikums A iestāsies tieši m reizes, bet iestāšanās un neiestāšanās
gadījumu secība nav fiksēta, tā varbūt jebkura. Tad iepriekšējā varbūtība ir
jāpareizina ar kombināciju skaitu, ko var sastādīt no n
elementiem pa m elementiem,
Līdz ar to:
![]() . (2.21)
. (2.21)
Ievietojot
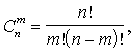
iegūstam Bernulli formulu šādu uzdevumu risināšanai
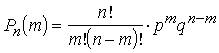 . (2.22)
. (2.22)
Formulu vislabāk ilustrēt ar klasisko
teoriju. Iedomāsimies, ka vienlaikus met trīs spēļu kauliņus un spēles iznākums
ir atkarīgs no tā, cik reizes uzkrīt sešnieks.
Sešnieks šajā situācijā var uzkrist
3x, 2x, 1x un nevienu reizi. To
varbūtības saskaņā ar Bernulli formulu ir šādas:
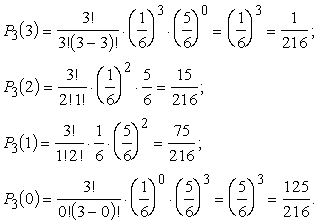
Atgadinām, ka ![]() .
.
Saskaitot iegūtos rezultātus, summā
jādabū viens. Ja uzdevumā ir vārdi
''vairāk kā'', ''mazāk kā'', ''no ... līdz'', jānovērtē, kuri saliktie notikumi
atbilst uzdevuma nosacījumiem, un attiecīgās varbūtības jāsaskaita.
Bernulli formula ir vienāda
ar attiecīgo Ņutona binoma izvirzījuma locekli, ja binomu ņem pakāpē n, kas
atbilst izmēģinājumu skaitam.
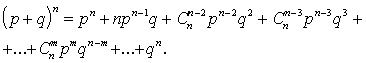 (2.23)
(2.23)
Tātad
Bernulli formula ir Ņutona binoma izvirzījuma vispārējais
loceklis.
Ja
n nepārsniedz 50 - 90, vajadzīgos
faktoriālus var aprēķināt tieši, izmantojot zinātniskam vai inženierdarbam
domātu kabatas skaitļotāju. Tad grūtības nerodas, vienīgi dažkārt kā
starprezultāti jāfiksē ļoti lieli skaitļi.
Ja
n sasniedz un pārsniedz šīs robežas,
tad Ņutona binomu tuvināti var aizstāt ar normālā sadalījuma likumu, pie kam
tuvinājums ir labāks, ja n
ir lielāks skaitlis. Normālo sadalījumu aplūkosim 4. nodaļā.
Tuvināto
metožu lietošana ir sevišķi nepieciešama, ja uzdevuma ietvaros, kuru vajadzētu
risināt ar Bernulli formulu, šo formulu vajadzētu lietot daudzkārtīgi.