12. Kovariācijas analīze

 

12.1. Uzdevuma  nostādne  un  kovariācijas  analīzes  veidi

 

12.1.1. Dispersijas, regresijas un kovariācijas analīzes specifika

 

            Salīdzināsim savā starpā dispersijas un regresijas - korelācijas analīžu iespējas.

            Dispersijas analīze pētī galvenokārt atributīvu pazīmju sakarības, noskaidrojot šo sakarību statistisko nozīmību. Ar dispersijas analīzi var pētīt arī kvantitatīvu pazīmju sakarības, uzlūkojot izdalītās variācijas grupas par kvalitatīvi atšķirīgām, tātad nosacīti par atributīvām. Bet tad dispersijas analīze nav tik efektīva kā regresijas - korelācijas analīze, jo nedod iespēju izstrādāt sakarību modeli. Citiem vārdiem, dispersijas analīze neprasa uzrādīt metriskas attiecības izdalīto grupu jeb pazīmes varianšu starpā.Tā ir viņas priekšrocība.

            Regresijas un korelācijas analīze pētī kvantitatīvu pazīmju sakarības. Atributīvām pazīmēm tā nav piemērota, jo neeksistē metriskas (izmērāmas) attiecības atributīvas pazīmes varianšu starpā, kas, lietojot regresijas un korelācijas analīzi, ir nepieciešams. Toties, pētījot kvantitatīvu pazīmju sakarības, regresijas - korelācijas analīze dod iespēju nevien novērtēt sakarību nozīmību, ko dod arī dispersijas analīze, bet arī aprēķināt sakarību modeli un noteikt sakarību ciešumu. Dispersijas analīze tādas iespējas nedod. Tādēļ, pētījot kvantitatīvu pazīmju sakarības, regresijas un korelācijas analīzei ir lielas priešrocības.

            Ja interesējošo rezultatīvo pazīmi vienlaikus ietekmē tiklab atributīvas kā kvantitatīvas faktorālas pazīmes, tad regresijas un korelācijas analīzi tiešā veidā nevar izmantot. Dispersijas analīze tiešā veidā ir lietojama, bet tā nedod iespēju izstrādāt skaitlisku modeli kvantitatīvo pazīmju sakarībām. Tādēļ dispersijas analīzes patstāvīgs lietojums šādā gadījumā ir maz efektīvs.

            Kovariācijas analīze zināmā mērā savieno dispersijas un regresijas analīzes īpašības. Tādēļ tā ir vispiemērotākā sakarību pētīšanas un modelēšanas metode, ja sakarībās kā faktori vienlaikus ieiet tiklab atributīvas, kā arī kvantitatīvas pazīmes.

            Atkarībā no uzdevuma satura lieto vienu no divām kovariācijas analīzes pamatformām.

            Ja pētījumā svarīgākās ir kvantitatīvās pazīmes, tad kovariācijas analīzē dominē regresijas analīzes algoritms un galīgos rezultātus iegūst modificēta regresijas vienādojuma veidā. Darba gaitā tiek izslēgta atributīvo pazīmju līdzietekme, kura, ja tai nepievērstu vērību, varētu izkropļot interesējošo kvantitatīvo pazīmju sakarības.

            Ja pētījumā svarīgākās ir atributīvās pazīmes, tad kovariācijas analīzes algoritmā dominē dispersijas analīzes metodes, un rezultātā iegūst dispersijas analīzei raksturīgus secinājumus. Tikai darba gaitā tiek izslēgta kvantitatīvo pazīmju līdzietekme, kura traucē pētīt atributīvo pazīmju ietekmi uz rezultatīvo pazīmi.

            Ekonomikas pētījumos parasti lielāka interese ir par kvantitatīvo pazīmju sakarībām. Tādēļ turpmākais kovariācijas analīzes apskats atbilst pirmai pamatformai. Otrai pamatformai varētu būt nozīme dažos socialoģijas pētījumos.

 

 

12.1.2.  Vienkārša kovariācijas analīzes uzdevuma  nostādne

 

            Kovariācijas analīzi ekonomikā bieži lieto, ja ir nepieciešams modelēt kvantitatīvas sakarības pēc vairāku gadu datiem. Atsevišķus gadus tad uzlūko par vienas atributīvas pazīmes (laika) variantiem.

            Pieņemsim, ka pēc 20 lauksaimniecības uzņēmumu viena gada datiem ir iegūts regresijas vienādojums, kurš atspoguļo minerālmēslojuma ietekmi uz graudaugu ražību    .

            Ja ir nepieciešams palielināt modeļa parametru statistisko nozīmību, piemēram, lai tos izmantotu kā normatīvus prognozēšanā, ir jāpalielina statistiskā kopa (datu apjoms), pēc kuras šie parametri aprēķināti. Tad, saskaņā ar lielā skaita likuma darbību, aprēķinātie parametri kļūst statistiski nozīmīgāki un stabilāki.

            Pētījumam izmantojamo datu apjomu var palielināt, ietverot analīzē lielāku uzņēmumu skaitu. Bet samērā bieži tas nav iespējams vai nu tādēļ, ka šajā nozarē vairāk uzņēmumu vienkārši nav, vai arī tādēļ, ka, palielinot kopu teritorijā, tā pārsniedz pieļaujamo iekšējo neviendabību. Tādā gadījumā apstrādājamo datu kopu var palielināt, ņemot datus par esošajiem uzņēmumiem nevis  par vienu, bet par diviem vai vairākiem gadiem. Katra uzņēmuma - gada datus uzlūko par patstāvīgu novērojumu.

            Piemēram, ņemot vienu gadu vecākus datus par iepriekš minētajiem 20 lauksaimniecības uzņēmumiem, iegūstam regresijas vienādojumu , kurš ir gan līdzīgs iepriekšējam, tomēr no tā atšķiras.

            Lai izveidotu šo pašu sakarību modeli pēc divu gadu datiem, var rīkoties dažādi. Trīs vienkāršākie paņēmieni ir šādi.

 

            1. Aprēķina regresijas vienādojumu par katru gadu atsevišķi, izskaitļo visu parametru vidējās vērtības un no tām sastāda ''vidējo'' vienādojumu. Tā rīkojas, ja uzdevuma risinājums neprasa matemātisku pamatojumu un precizitāti. Kā atrastais vienādojums atbilst vismazāko kvadrātu metodei, nav zināms.

            2. Abu divu gadu datus apvieno kopējā masīvā un apstrādā ar parastajām regresijas un korelācijas analīzes metodēm. Tā var rīkoties tad, ja visu mainīgo lielumu aritmētiskie vidējie laika gaitā ir maz mainījušies. Bet, ja vidējo lielumu izmaiņas ir lielas, tās būtiski ietekmē regresijas parametru vērtības, novedot pat pie statistiskiem paradoksiem. Paradokss izpaužas tā, ka, piemēram, regresijas koeficients, kurš aprēķināts pēc divu gadu kopējiem datiem ir ārpus variācijas apgabala, ko veido atsevišķu gadu koeficienti, piemērā mazāks par 8,28 vai lielāks par 9,72.

            3. Lai izvairītos no loģiski nepieņemamiem rezultātiem un vienlaikus saglabātu matemātisku pamatotību, minēto uzdevumu var risināt, izmantojot kovariācijas analīzi.

            Kovariācijas analīzes rezultātā iegūst vienu regresijas vienādojuma vidējo formu, kas modelē kvantitatīvo pazīmju sakarības pēc vairāku gadu datiem un tā saucamos gada efektus skaitlisku konstanšu veidā katram gadam atsevišķi. Šīs konstantes secīgi var pieskaitīt vienādojuma vidējās formas brīvajam loceklim. Tādējādi iegūst tik vienādojumu, cik ir analīzē izmantoto gadu. Šiem vienādojumiem ir viens un tas pats regresijas koeficients, bet atšķirīgi brīvie locekļi.

            Var aprēķināt virkni sakarību ciešuma radītāju un parametru izlases kļūdu.

            Citos uzdevumos datu masīva kvalitatīvās grupas var veidot teritoriāli areāli (novadi, rajoni), vai citādi kvalitatīvi atšķirīgas kopas (piemēram, lauksaimniecībā - statūtsabiedrības, zemnieku saimniecības, piemājas saimniecības).

 

 

12.1.3.  Kovariācijas analīzes ģeometriska interpretācija un būtība

 

            Kovariācijas analīzes būtību var uzskatāmi parādīt grafiskā attēlā (12.1. attēls).

           

Vienā korelācijas diagrammā ir iezīmēti divi korelācijas lauki, kuri atbilst divu gadu datiem un attēlo vienu un to pašu mainīgo sakarības, piemēram, mēslojums - ražība. Atbilstoši katram korelācijas laukam ir aprēķināta un iezīmēta attēlā regresijas taisne. Regresijas taisnēm abos gadījumos ir aptuveni vienādi leņķa koeficienti, jo faktora ietekme jeb saimnieciskā atdeve ir maz mainījusies.

            Tālāk pieņemam, ka otrajā gadā, salīdzinot ar pirmo, sakarā ar saimniecisko progresu, ir izmantotas ievērojami lielākas mēslojuma devas. Toties metereoloģiskie apstākļi ir bijuši neizdevīgāki. Tādēļ rezultatīvās pazīmes (ražības) vidējais lielums abos gados atšķiras maz. Apvienojot abu gadu datus vienā masīvā un pēc tiem rēķinot regresijas taisnes vienādojumu, iegūstam taisni, kuras leņķa koeficients ir būtiski mazāks nekā atsevišķo gadu taišņu leņķu koeficienti, veidojot statistisko paradoksu.

 

 

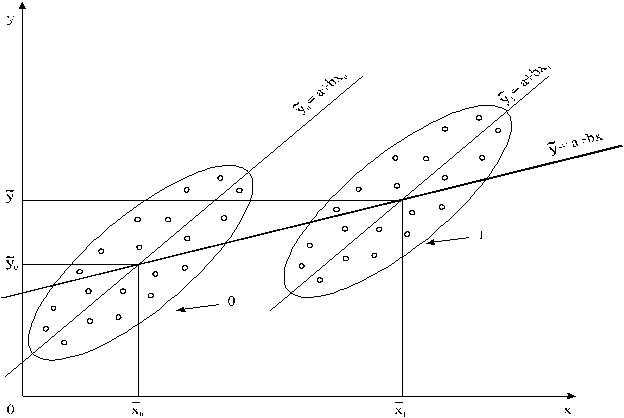
12.1. attēls. Divu korelācijas lauku apvienošanas problēma : 0 - bāzes gadā, 1 - pārskata gadā.

 

            Lai vidējo lielumu izmaiņas neietekmētu regresijas un korelācijas rādītājus, domās izdarām šādas darbības. Uzzīmējam uz caurspīdīga papīra katra gada korelācijas lauku atsevišķi. Pēc tam uzliekam vienu attēlu uz otra un pārbīdām vienu pret otru tā, lai, saglabājoties koordinātu asu paralelitātei sakristu abu korelācijas lauku viduspunkti, proti , kas aprēķināts pēc pārskata un  ,  kas aprēķināts pēc bāzes gada datiem. Tādā gadījumā, ja laika gaitā nebūs izmainījies   un   sakarību raksturs, abi korelācijas lauki pareizi uzklāsies viens uz otra, veidojot kopēju masīvu. Pēc šāda kopējā korelācijas lauka aprēķināta regresijas taisne pareizi atspoguļos reālās sakarības, novēršot statistiskos paradoksus un citas sakarību rādītāju nobīdes vidējo lielumu izmaiņu rezultātā. Pēdējo ietekmi atspoguļos speciāli rādītāji, t.s. gradāciju efekti, piemērā - gadu efekti.

            Šādu nostādni matemātiski realizē tā, ka kopējā masīvā neapvieno vis datu summas, kvadrātu un pāru reizinājumu summas   , bet gan noviržu, to kvadrātu un noviržu reizinājumu summas. Pie tam novirzes ņem nevis no kopējiem vidējiem, bet gan no attiecīgu gadu vidējiem.

Tādējādi par katru gadu atsevišķi aprēķina:

 

                      ,

 

kur   un  - attiecīgā gada vidējie, un pēc tam summē par visiem gadiem.

 

            No iegūtām kopsummām sastāda normālvienādojumu sistēmu, un to atrisina parastā kārtībā.   Šīs darbības izsaka kovariācijas analīzes būtību.

 

12.1.4. Kovariācijas analīzes veidi

 

            Kovariācijas analizes modeļus un līdz ar to analīzes veidus klasificē pēc :

            - analīzē iekļauto atributīvo pazīmju skaita, izšķirot vienas un vairāku atributīvo pazīmju
                kompleksus;

            - analīzē iekļauto kvantitatīvo pazīmju skaita, izšķirot vienkāršo un daudzfaktoru
                kovariācijas analīzi;

            - sakarību formas, izšķirot lineāro un nelineāro kovariācijas analīzi.

            Apstrādājot vienkopus vairāku gadu datus, iegūstam viena atributīvā faktora kompleksu. Vienīgais atributīvais faktors ir laiks ar tik gradācijām, cik ir ņemto gadu.

            Kvantitatīvās pazīmes ekonomikas pētījumos parasti ir jāņem vairākas, tādēļ visbiežāk ir jālieto daudzfaktoru kovariācijas analīze. Sakarību formu parasti izvēlās lineāru kā vienkāršāko un pietiekami tuvu īstajai reālai sakarību formai.

            Tā kā mums nav iespējams aplūkot visus kovariācijas paveidus, aplūkosim pēc mūsu domām vajadzīgāko - lineāru daudzfaktoru kovariācijas analīzi ar vienu atributīvo faktoru. Pieņemam, ka lasītājam ir zināma daudzfaktoru regresija un korelācija. Vienkāršo kovariācijas analīzi var saprast kā dauzfaktoru analīzes speciālu gadījumu, ja kvantitatīvo faktoru skaits ir viens.

 

 

12.2. Kovariācijas analīzes modelis un normālvienādojumu sistēma

 

12.2.1. Kovariācijas analīzes modelis

 

            Aplūkojam viena atributīva faktora lineāru kvantitatīvu daudzfaktoru kovariācijas analīzi. Interpretācijas vienkāršošanai pieņemam, ka atributīvais faktors ir laiks ar gadu gradācijām, kuras nav metriski samērojamas. Citos uzdevumos atributīvā pazīme var būt arī teritorijas, nozares vai jebkura cita pazīme.

            Tātad  pēc vairāku gadu datiem ir jāaprēķina daudzfaktoru regresijas vienādojums

 

             ,                                     (12.1)

kur     teorētiskais jeb aprēķinātais rezultatīvās pazīmes lielums,    

         faktorālās pazīmes,

         regresijas parametri, aprēķināti ar kovariācijas analīzi.

 

Vienādojumu (12.1) sauc par regresijas vienādojumu vidējo formu, bet dažreiz, lai uzsvērtu metodi, par kovariācijas vienādojumu.

            Lai labāk atklātu metodes specifiku, modelī parāda arī atributīvās pazīmes gradāciju (resp. gadu) efektus. Parasti tajā ietver arī neizskaidroto jeb gadījuma komponenti un faktorālās pazīmes izsaka novirzēs no vidējiem lielumiem. Tādā gadījumā ir jāaprēķina šādas izteiksmes parametri:

 

,        (12.2)

 

kur

i -- kopas vienības (saimniecības)  numurs,

j -- gradācijas (gada) numurs,

g -- faktora numurs; ja ir nepieciešams uzrādīt vispārīgā veidā

      divu aišķirīgu faktoru numurus, izmanto otru simbolu h ,

m -- faktoru skaits ( arī pēdējā faktora Nr;  g = m ).

Tādējādi:

 -- rezultatīvās pazīmes faktiskais lielums i vienībā j -jā gadā;

   -- rezultatīvās pazīmes kopējais vidējais; punkti indeksā nozīmē šo

           numuru trūkumu, faktoru indeksus uzrādīt nav vajadzīgs;

 --   g - faktora daudzfaktoru regresijas koeficients, kas aprēķināts ar        

            kovariācijas analīzi;

  -- j -tās gradācijas (gada) efekts, skaitliska konstante, ko aprēķina    

            katrai  gradācijai atsevišķi;

   -- rezultatīvās pazīmes faktiskā lieluma novirze no teorētiskā, i  -ai  

             vienībai j - jā gadā, tātad    .

             To sauc par analīzes atlikumu, gadījuma komponenti.

 

            Tā kā   katrai gradācijai (gadam) ir atšķirīgs, tad šādu modeļu (12.2) ir tik daudz, cik ir gradāciju (gadu). Tādēļ arī izteiksmes kreisajā pusē pie rezultatīvās pazīmes simbola    ir indekss j ;   j = 1 , ... , k.

 

 

12.2.2. Dažas kovariācijas modeļa īpašības

 

            Kovariācijas modeļa (12.2)  parametrus aprēķina tā, lai modelim būtu šādas īpašības.

 

            1. Neizskaidroto  noviržu algebriskā summa katras gradācijas (gada) ietvaros ir nulle.

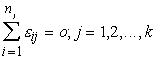                                                            .                                         (12.3)

 

Teorētiskās rezultatīvās pazīmes lielumus, kas ir noviržu  aprēķināšanas pamatā, rēķina pēc atsevišķu gradāciju (gadu) vienādojumiem.

            Ja teorētiskos lielumus rēķina pēc vienādojuma vidējās formas (12.1), tad nulles īpašības ir spēkā tikai visā daudzgradāciju (daudzgadu) teritoriālajā kopumā:

 

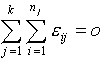                          .                                                       (12.4)

 

            2.Katra faktora efektu summa visā kopumā (daudzgadu teritoriālajā kopumā) ir nulle.

 

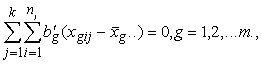                               (12.5)

 

kur

        k -- gradāciju (gadu) skaits,

       -- kopas vienību (saimniecību) skaits j - jā  gradācijā (gadā).

Summēšana pēc  i  nozīmē summēšanu pa vienībām atsevišķas gradācijas (gada) ietvaros; summēšana pēc  j - iepriešējo summu saskaitīšana visās gradācijās (gados).

            3. Gradāciju (gadu) efektu summa ir  nulle. Par svariem jāņem vienību (saimniecību) skaits katrā gradācijā (gadā):

 

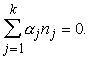                                                              (12.6)

            Ja vienību skaits visās gradācijās ir vienāds, svaru lietošana nav vajadzīga. Pašu gadu efektu summa ir nulle.

            Kovariācijas analīzes lietošanas priekšnoteikums prasa, lai kvantitatīvo faktoru un rezultatīvās pazīmes sakarību raksturs visās gradācijās (gados) saglabātos nemainīgs. Tādēļ pirms kovariācijas analīzes uzsākšanas  ir lietderīgi aprēķināt parastos daudzfaktoru regresijas vienādojumus par katru gradāciju (gadu) atsevišķi. Šādu vienādojumu atbilstošie regresijas koeficienti nedrīkst būtiski atšķirties. Atšķirību statistisko nozīmību var novērtēt ekspertīzes ceļā vai pārbaudot attiecīgās nulles hipotēzēs. Vienādojuma brīvie locekļi var atšķirties būtiski. Ja regresijas koeficienti atšķiras būtiski, tad sakarībām katras gradācijas (gada) ietvaros ir cits raksturs un nekāda metode nedod iespēju atrast kopēju sakarību modeli. Tad kovariācijas analīzes lietošana vispārīgā gadījumā nav pamatota.     Šo priekšnoteikumu neievēro, un kovariācijas analīzi tomēr lieto tad, ja ekspertīzes ceļā novērtē, ka atsevišķo gradāciju (gadu) vienādojumu koeficienti atšķiras nevis tādēļ, ka izmainījies sakarību raksturs, bet gan novērošanas un citu kļūdu rezultātā.

 

 

12.2.3. Kovariācijas analīzes normālvienādojumu sistēma

 

            Kovariācijas modeli  (12.2)  aprēķina tā, lai rezultatīvās pazīmes faktisko lielumu  noviržu kvadrātu summa no tās pašas pazīmes teorētiskajiem lielumiem būtu minimāla.

            Teorētiskos lielumus savukārt aprēķina, ņemot vērā gradāciju efektu    vai, kas ir tas pats, pēc atsevišķu gradāciju vienādojumiem.

            Tātad izdarot minimizāciju

 

 

simbola    vietā jāliek kovariācijas modeļa (12.2) labā puse, bez . Kā redzams visi mainīgie modelī ir izteikti novirzēs no gradāciju (gadu) vidējiem. Tālāk normālvienādojumu sistēmas izvedums ir analogs parastajam.

            Lai vienkāršotu pierakstu, noviržu, to kvadrātu un pāru reizinājumu summas apzīmē ar simbolu Q, izmantojot vajadzīgās norādes indeksu formā.

            Citiem vārdiem, kovariācijas analīzē atsevišķu gradāciju (gadu) datu masīvus apvieno, aprēķinot un summējot novirzes no šo gradāciju vidējiem lielumiem, tāpat aprēķina to kvadrātus un pāru reizinājumu summas, t. s. krossummas. Tādēļ par katru gradāciju atsevišķi ir jāaprēķina šādi lielumi.

            Rezultatīvās pazīmes katras gradācijas vidējie:

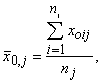
                                                 (12.7)

kur j - gradācijas (gada) indekss, i - novērojuma (saimniecības) indekss;  rēķinot gradācijas vidējos, tas zūd.

 

            Visu faktorālo pazīmju gadu vidējie:

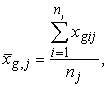
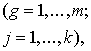                                              (12.8)

 

kur   g  - faktorālās pazīmes indekss; pavisam m faktorālo pazīmju, tātad   

              jāaprēķina šāds skaits vidējo;

        - vienību (saimniecību) skaits j - jā gradācijā.

 

            Noviržu kvadrātu summas visām gradācijām rezultatīvai pazīmei un visām

faktorālām pazīmēm:

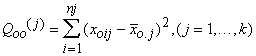                                            (12.9)

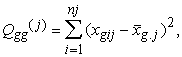
                                         (12.10)

 

            Noviržu    skaits ir  k  atbilstoši gradāciju skaitam, bet noviržu  

skaits ir  m k - atbilstoši gradāciju un faktoru skaita reizinājumam.

            Atsevišķu gradāciju jaukto noviržu reizinājumu summas:

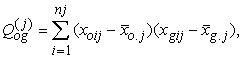
                           (12.11)

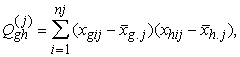
                   (12.12)

           

            Tā kā      tad lielumus  h > g  patstāvīgi neizskaitļo.

 

            Tālāk atsevišķo gadu summas (12.9) - (12.12) summē pa visām gradācijām (gadiem):

 

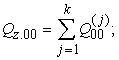                                                                              (12.13)

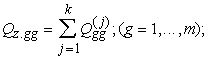                                                        (12.14)

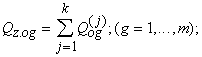                                                          (12.15)

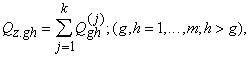                                              (12.16)

kur z - dispersijas analīzē pieņemtais atlikuma (gadījuma) komponents, simbols.

            Ievērojot formulās (12.13) - (12.16) definētos simbolus, kuru saturs tālāk atklāts formulās (12.9) - (12.12), normālvienādojuma sistēmu kovariācijas analīzei var pierakstīt šādi:

 

     ^{...       ...       ...      ...       ...      ...      ...}

     ^{...       ...       ...      ...       ...      ...      ...}

                (12.17)

 

            Sistēmas koeficientu matrica ir simetriska pa galveno diagonāli, jo  tādēļ šos lielumus patstāvīgi izskaitļot nevajag.

            Sistēmu (12.17) matemātiski pierāda līdzīgi parastai normālvienādojumu  sistēmai, tikai teorētiskos lielumus definē kā aprēķinātus ar kovariācijas analīzi.

            Sistēmu (12.17) var atrisināt ar jebkuru paņēmienu. Kā parasti, var ieteikt izmantot inverso matricu, jo tās elementi atvieglo dažādu sakarību ciešuma un izlases kļūdu rādītāju izskaitļošanu.Sistēmas atrisinājums dod regresijas vienādojuma vispārīgās formas (12.1) koeficientus. Brīvais loceklis ir jāaprēķina atsevišķi ar šādu formulu:

 

                                                (12.18)

kur    

          visas daudzgradāciju (daudzgadu) kopas mainīgo vidējie lielumi.

 

 

12.2.4. Skaitļošanas darba vienkāršošana, izmantojot momentu metodes formulas

 

            Formulas (12.9) - (12.18) labi atklāj kovariācijas analīzei izmantojamās sākotnējās informācijas sagatavošanas loģiku. Tās izsaka šīs metodes būtību. Bet viņas nav ērtas praktiskam skaitļošanas darbam. Bez tam, ja vairāku gadu datus uzkrāj pakāpeniski dinamikas rindu veidā vai izmantojot automatizētas datu bankas, daudz ērtāk fiksēt sākotnējo datu, to kvadrātu  un pāru reizinājumu summas nekā attiecīgās noviržu kvadrātu un reizinājumu summas. Tādēļ darbam ļoti ērtas ir formulas, kas dod iespēju izskaitļot vajadzīgās noviržu kvadrātu un reizinājumu summas, izmantojot sākotnējo datu, to kvadrātu un reizinājumu summas. Vajadzīgās formulas iegūst, pareizinot ar kopas vienību skaitu  n  dispersijas momentu formulas abas puses un tāpat kovariācijas formulas abas puses.

           

            Atgādinam no statistikas teorijas zināmās momentu metodes formulas.

 

            Dispersija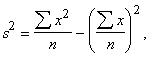                                

 

            noviržu  kvadrātu summa          

 

 

 

            Aprēķini jāizdara par katru gadu atsevišķi. Tādēļ sekojošās formulas ir pierakstītas  j- jam gadam.

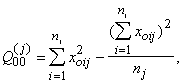                                                  (12.19)

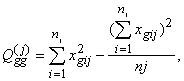                                                  (12.20)

 

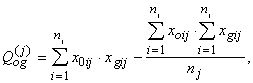                                 (12.21)

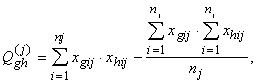                                (12.22)

 

            Formulu (12.19) - (12.22) pēdējos locekļus parasti sauc par korekcijas vai redukcijas locekļiem pārejai no vienas atskaites sistēmas uz otru un dažkārt apzīmē ar īpašu simbolu. Minētās formulas realizē pāreju no parastajām krossummām uz noviržu krossummām.

            Ja izmanto vairāku gadu datus, tad atsevišķo gadu summas (12.19) - (12.22) tālāk summē pa visiem gadiem saskaņā ar formulām (12.13) - (12.16), pēc tam sastādot normālvienādojumu sistēmu (12.17).

 

 

12.2.5. Kovariācijas analīzes piemērs un rezultātu interpretācija

 

            Pieņemam, ka pēc pārskata gada datiem ir aprēķināts šāds divu faktoru vienādojums

 

 

kas raksturo, kā graudaugu ražību   ietekmē tīrumu kvalitāte   un minerālmēslojumu devas     Aprēķiniem izmantotās krossummas ir šādas:

 

       ,

      

                

 

        n=20   (12.1. tabulas 7. aile).

 

 

 

 

 

12.1 tabula

 

Sakotnējās informācijas sagatavošana daudzfaktoru kovariācijas analīzei

 

Tabulā uzrādīto lielumu vienkāršoti simboli (skat.  formulas 19. -  22.)			Pirmais  (iepriekšējais)  gads			Otrais (pārskata)  gads			Noviržu kvadrātu	Abi  gadi  kopā  (abu gadu tieša apvienošana)
Summas, kvadrātu un pāru reizināju-mu summas	Redukcijas lielumi	Noviržu kvadrātu un reizināju-mu summas (1. - 2. aile)	Summas, kvadrātu un pāru reizinā-jumu summas	Redukci-jas lielumi	Noviržu kvadrātu un reizinā-jumu summas (4. - 5. aile)	Summas, kvadrātu un pāru reizinā-jumu summas	Redukci-jas lielumi	Noviržu kvadrātu un reizinā-jumu summas (7. - 8. aile)	un reizinā-jumu summas kovariā-cijas analīzei (6. + 9. aile)	Summas, kvadrātu un pāru reizinā-jumu summas (4. + 7. aile)	Redukci-jas lielumi	Noviržu kvadrātu un reizinā-jumu summas (11.- 12. aile)
1	2	3	4	5	6	7	8	9	10	11	12	13
	-	-	576	-	-	666	-	-	-	1242	-	-
	-	-	800	-	-	800	-	-	-	1600	-	-
	-	-	37,3	-	-	42	-	-	-	79.3	-	-
			17672	16588,8	1083,2	23802.6	22177.8	1624.8	2708.8	41475	38564.1	2910.9
			33180	32000	1180	33180	32000	1180	2360.0	66360	64000	2360
			74,95	69,5645	5,3855	106.969	88.2	18.769	24.1545	181.92	157.212	24.708
			23920	23040	880	27715.8	26640	1075.8	1955.8	51636	49680	1956
			1126,6	1074,24	52,36	1554.09	1398.6	155.49	207.85	2680.7	2462.3	218.4
			1525,9	1492,0	33,9	1753.61	1680	73.61	107.51	3279.5	3172	107.5

 

             Pieņemam, ka šādi aprēķini ir veikti jau otro gadu. Iepriekšējā gadā pēc to pašu saimniecību datiem ir iegūts analogs vienādojums:

 

.

 

Ir saglabātas arī aprēķinos izmantotās krossummas.

 

 

 

 

 

              n= 20 (12.1.tabulas 4. aile).

 

            Salīdzinot abus regresijas vienādojumus, redzam, ka attiecīgie regresijas koeficienti ir samērā līdzīgi. Pētīto faktoru ietekme uz ražību, acīmredzot, nav mainījusies. Lai noskaidrotu statistiski drošākus  šos ietekmes rādītājus, kurus tad varētu izmantot kā normatīvus, nolemjam tos aprēķināt, izmantojot vienlaikus abu gadu datus.

            Tā kā abu vienādojumu brīvie locekļi ir ievērojami atšķirīgi, abu datu masīvu tieša apvienošana, summējot uzrādītās summas, apmierinošus rezultātus parasti nedos. Lai pārliecinātos par teikto, izdarām tādus aprēķinus, summējot 12.1. tabulas 4. un 7. aili un rezultātus uzrādot 11. ailē. Sastādot no šīm summām normālvienādojuma sistēmu un to atrisinot, iegūstam

 

 

            Otrais regresijas koeficients dod statististisku paradoksu. Minerālmēslojuma ietekmes rādītājs pēc divu gadu datiem  6,53  ir lielāks, nekā abos šajos gados, ņemot tos atsevišķi: 6,23  un  6,14.

            Tādēļ datu masīvi ir jāapvieno, summējot nevis sākotnējās summas, bet noviržu kvadrātu un to reizinājumu summas. Citiem vārdiem, ir jālieto kovariācijas analīze. Sākotnējās informācijas sagatavošanai nepieciešamie aprēķini ir sakopoti 12.1. tabulā. Tās 4. un 7. ailē ir sākotnējo datu krossummas, 5. un 8. ailē ir   parādīti redukcijas locekļi saskaņā ar formulu ( 12.19 - 12.22) labo pušu pēdējiem locekļiem. Tos atņemot no pašām krossummām ( tabulas 4. un 7. aile ) izpildām visas formulās (12.19 - 12.22) prasītās darbības. Noviržu kvadrātu un reizinājumu summas (tabulas 6. un 9. aile) summējot pa abiem gadiem, izpildām formulās (12.13 - 12.16) paredzētās darbības (skat. tabulas 10. aili ). Pēc pēdējās ailes datiem arī tiek sastādīta normālvienādojuma sistēma kovariācijas analīzei.

                        

 ,                      

 

 

            To atrisinot iegūstam, ka   =0,547785,    =6,16712.                   

Lidz ar to kovariācijas vienādojums novirzēs no vidējiem ir šāds:

 

 

 

            Brīvo locekli aprēķina pēc formulas (12.18), vispirms izskaitļojot vispārējos vidējos lielumus:

 

 

 

            Līdz ar to

 

 .

 

            Viss vienādojums saskaņā ar modeli ir šāds:

 

 .

   

 

 

 

12.2.6. Gradāciju efekti un gradāciju  vienādojumi

 

            Regresijas vienādojuma vidējā forma labi atspoguļo sakarības vispārējo raksturu. Šī vienādojuma koeficienti raksturo faktoru vidējo ietekmi uz rezultatīvo pazīmi. Vienādojuma vispārīgo formu var izmantot normatīvajā analīzē un prognozēšanā.

             Analīzes vajadzībām atsevišķu gradāciju (piemērā - gadu) ietvaros vienādojuma vispārīgā  forma nav piemērota. Ja pēc tās izskaitļo teorētisko ražību saimniecībām, tad vienam gadam iegūstam sistemātiski palielinātus, bet otram  samazinātus lielumus. Tāda parādība izskaidrojama ar to, ka atsevišķu gadu vidējā ražība  nesakrīt ar divu gadu vidējo ražību. No matemātikas viedokļa vienādojuma vidējā forma nenodrošina noviržu   nulles īpašību, summējot atsevišķu gadu ietvaros (skat. 12.4.). Tādēļ analīzes vajadzībām izmanto  gradāciju (piemērā - atsevišķu gadu)  vienādojumus, kuri no vidējās formas atšķiras ar t. s. gradācijas ( piemērā - gada ) efektu.

 

            Gradācijas efektu j - jai gradācijai    aprēķina ar šādu formulu  :

 

           (12.23)

 

kur

-	vienas  j  - tās gradācijas (gada) vidējie lielumi pirmajā indeksā uzrādītajiem mainīgiem lielumiem;
-	vispārīgie vidējie visās gradācijās.

 

            Aprēķināsim gada efektus pēc formulas (12.23) iepriekš aplūkotajam  piemēram.

 

;

 

 

            Tā kā aplūkojam tikai divus gadus un saimniecību skaits abos gados ir vienāds, tad gadu efekti skaitliski sakrīt, bet atšķiras ar zīmēm.

            Gadu efektus secīgi pieskaitot regresijas vienādojuma vidējai formai, iegūstam atsevišķu gadu vienādojumus. Vidējā forma bija :

 

 

 

            Gadu vienādojumi:

 

           

 

 

            Pēc šiem vienādojumiem aprēķinātās teorētiskās ražības nodrošina pozitīvo un negatīvo noviržu līdzsvarošanos katra gada ietvaros, skat. formulu (12.4). Tādēļ šie vienādojumi ir piemēroti analīzes vajadzībām.

            Efekti  raksturo katra gada specifisko apstākļu ietekmi uz ražību, kuru rezultātā  tā novirzās no vairāku gadu vidējās ražības.

 

12.3. Kovariācijas  sakarību  ciešuma  rādītāji

 

12.3.1. Sakarību ciešuma rādītāju veidi

 

            Tā kā kovariācijas analīzē vienlaikus izmanto atributīvus un kvantitatīvus faktorus, tad, vadoties no pētījuma satura, var izšķirt vairākus sakarību ciešuma rādītājus:

 

            1. Kvantitatīvajām pazīmēm ar rezultatīvo pazīmi, pēc tam kad atributīvo pazīmju līdzietekme ir izslēgta.

            2. Atributīvajām pazīmēm ar rezultatīvo pazīmi, pēc tam, kad kvantitatīvo pazīmju līdzietekme ir izslēgta.

            3. Visām faktorālām pazīmēm un pētītai rezultatīvai pazīmei.

 

            Ja pētījumā svarīgākās ir kvantitatīvās pazīmes, tad parasti izskaitļo tikai pirmās un dažreiz vēl trešās grupas rādītājus.

No formas viedokļa sakarību ciešuma rādītājus kā parasti iedala trīs grupās.

 

            1. Bāzes rādītāji, kurus izmanto citu rādītāju izskaitļošanai. Te jāpieskaita neizskaidrotā, izskaidrotā un kopējā rezultatīvās pazīmes noviržu kvadrātu summa, neizskaidrotā, izskaidrotā un kopējā rezultatīvās pazīmes dispersija. Šo lielumu skaitliskās vērtības ir atkarīgas no rezultatīvās pazīmes mērvienībām, bet pašiem šiem rādītājiem nav pēc satura interpretējamas mērvienības (formāli sākotnējo datu mērvienības kvadrāts). Bāzes sakarību ciešuma rādītājus izmanto nosaukto un nenosaukto sakarību ciešuma rādītāju izskaitļošanai.

            2. Nosauktie sakarību ciešuma rādītāji ir vērtējuma standartkļūda un robežkļūda. Vērtējuma standartkļūdu atrod, aprēķinot kvadrātsakni no neizskaidrotās dispersijas, bet robežkļūdu  -  pareizinot standartkļūdu ar varbūtības koeficientu. Vērtējuma standartkļūdai un robežkļūdai ir rezultatīvās pazīmes mērvienība.

            3. Nenosauktie sakarību ciešuma rādītāji ir determinācijas un korelācijas koeficienti.

 

 

12.3.2. Neizskaidrotā noviržu kvadrātu summa un vērtējuma standartkļūda

 

            Visu sakarību ciešuma rādītāju pamatā, tāpat kā daudzfaktoru regresijas un korelācijas uzdevumos, ir neizskaidrotā  noviržu kvadrātu summa. Tās definīcijas formula ir šāda:

 

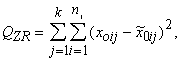                                       (12.24)

kur

             rezultatīvās pazīmes   teorētiskais lielums  i - tai kopas vienībai     

                 j - jā  gradācijā (gadā).

            Tātad    ir jāaprēķina pēc atsevišķu gradāciju (gadu) vienādojumiem. Noviržu kvadrātus summē vispirms katra gada ietvaros, pēc tam pa visiem gadiem. Ir izslēgta visa variācija, kas saistīta tiklab ar kvantitatīviem, kā arī ar kvalitatīvajiem faktoriem, kuri atspoguļoti modelī.

 

 

 

            Formula (12.24) izsaka aprēķināmā rādītāja būtību, bet nav ērta praktiskai izskaitļošanai. Praktiskam darbam ērtāka ir šāda pārveidota formula, analoga kā

lieto regresijas analīzē:

 

                              (12.25)

 

kur

   rezultatīvās pazīmes noviržu  no gradāciju (gadu) vidējiem                                                    lielumiem  kvadrātu summa;

 noviržu no gradāciju (gadu) vidējiem lielumiem reizinājumu                                       summas; nultā pazīme šeit visur ir rezultatīvā,

  regresijas koeficienti. Tie ir jāaprēķina ar kovariācijas analīzi.

 

            Piemēram vajadzīgās summas  var atrast 12.1. tabulā, bet regresijas koeficienti   un   bija aprēķināti 2.5. paragrāfā.

Līdz ar to

 

.

           

            Neizskaidroto dispersiju aprēķina, dalot šo noviržu kvadrātu summu ar novērojumu skaitu visā kompleksā . Vērtējuma standartkļūdu atrod, aprēķinot kvadrātsakni no neizskaidrotās dispersijas:

                                                              (12.26)

                                                            (12.27)

 

            Piemērā                       

                                               

 

            Tātad aprēķinātie atsevišķu gadu vienādojumi neizskaidro graudaugu ražības variāciju vidēji par 3,0 cnt/ha. Vērtējuma intervāls    ir saistīts ar varbūtību, kas saistās ar standartnovirzi. Lielas izlases gadījumā tā ir 0,68. Ja ir nepieciešams izveidot vērtējuma intervālu, kurš ir saistīts  ar citu varbūtību, jāatrod vērtējuma robežķūda, pareizinot standartkļūdu ar varbūtības koeficientu  Pēdējo, atbilstoši esošajam brīvības pakāpju skaitam un izvēlētai varbūtībai, nolasa Stjudenta tabulās.

            Var aprēķināt arī vērtējuma standartnovirzi no vidējā vienādojuma, bet to dara retāk.

 

 

 

 

 

 

 

12.3.3. Determinācijas un korelācijas koeficienti

 

            Determinācijas koeficientu aprēķina parastā kārtībā, dalot izskaidroto dispersiju ar visu dispersiju. Korelācijas koeficientu atrod, aprēķinot kvadrātsakni no determinācijas koeficienta.

            Izskaidroto dispersiju  parasti neaprēķina tieši, bet to atrod, atskaitot no kopējās dispersijas neizskaidroto dispersiju.

            Kovariācijas analīzē aprēķina vairākus determinācijas un korelācijas koeficientus. Viņi atšķiras ar to, ko ņem par visu jeb kopējo dispersiju determinācijas attiecībā (tāpat arī aprēķinot izskaidroto dispersiju).

            Ja interesē kvantitatīvo faktoru sakarību ciešums ar rezultatīvo pazīmi pēc tam, kad kvalitatīvā faktora (gradāciju) ietekme ir izslēgta, tad kopējo dispersiju (variācijas bāzi) aprēķina kā atsevišķu gradāciju dispersiju vidējo. Citiem vārdiem, ņem rezultatīvās pazīmes indviduālo datu novirzes nevis no kopējā, bet no atsevišķu gradāciju (gadu) vidējiem lielumiem. Starpgradāciju (gadu) variācija paliek ārpus pētījuma ietvariem.  Šādu nostādni realizē formulas

 

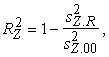                                                         (12.28)

un 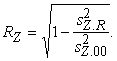                                                               (12.29)

 

            Skaitliskajam piemēram atbilstošā dispersija  bija izskaitļota iepriekš, bet   

 

Līdz ar to          

                        

                        

 

            Divu pētīto kvantitatīvo faktoru ietekme graudaugu ražības variāciju izskaidro aptuveni par 87% pēc tam, kad gadu, resp., meteoroloģisko faktoru ietekme ir izslēgta (determinācijas koeficients).

            Determinācijas un korelācijas koeficientus dažreiz ērtāk izskaitļot, izmantojot  nevis dispersijas, bet noviržu kvadrātu summas.

 

 Tā kā       

 

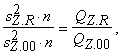
tad           .                                                                                                     (12.30)

 

  Piemērā                

 

 

            Ja pētījuma ietvaros interesē noteikt visu faktoru (kvantitatīvo un atributīvo) sakarību ciešumu ar rezultatīvo pazīmi, tad kopējo dispersiju aprēķina, ņemot indviduālo datu novirzes ap visa kompleksa rezultatīvās pazīmes kopējo vidējo lielumu jeb daudzgadu vidējo. Citādi formulas ir analogas iepriekšējām.

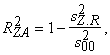                                                                                                                     (12.31)

 vai                                                                                                              (12.32)

 

            Attiecīgo korelācijas koeficientu atrod, aprēķinot kvadrātsakni no determinācijas koeficienta:

 

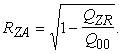                                                                                                                  (12.33)

 

            Skaitliskajam piemēram vajadzīgo   var nolasīt 12.1. tabulā, bet

 kā iepriekš.

 Lidz ar to   

                                                                                

                                                                                     

 

            Tā tad kvantitatīvo faktoru darbība un gadu īpatnības piemērā minētajās saimniecībās izskaidro ap 88% no graudaugu ražības variācijas. Attiecīgais daudzfaktoru korelācijas koeficients 0,937 rāda, ka sakarība  ir ciešas.

 

 

12.4. Izlases kļūdas un nulles hipotēžu pārbaude

 

12.4.1. Regresijas koeficientu izlases kļūdas

 

            Kovariācijas analīzei var izstrādāt visu modeļu parametru un teorētisko lielumu izlases kļūdu vērtēšanas sistēmu  tāpat kā parastās regresijas un korelācijas gadījumā. Īsi aplūkosim tikai regresijas koeficientu izlases kļūdas, jo tās parasti visvairāk interesē, noskaidrojot atklāto sakarību statistisko nozīmību. Tā kā  kopējam un gradāciju vienādojumiem koeficienti sakrīt, vērtējam tikai kopējā vienādojuma koeficientus.

            Regresijas koeficienta standartkļūdas formulas kovariācijas analīzei izveido līdzīgi kā parastās regresijas gadījumā. Tā kā  praktiskai lietošanai ir ērtāka formula, ka satur inversās matricas elementu, minēsim to:

                                                                                                                     (12.34)

kur      --  g -tā faktora regresijas koeficienta standartkļūdas kvadrāts;

            --  visu faktoru neizskaidrotās dispersijas nenobīdīts vērtējums.      

 

            Ja ir zināma parastā neizskaidrotā dispersija, tad 

                                                 

 

            (m -- faktoru skaits,  k -- gradāciju, resp., gadu skaits)

 -- normālvienādojumu sistēmas (12.7) koeficientu inversās matricas diagonālelements, kurš atrodas  g -jā rindiņā un stabiņā.

 

            Analizējamam skaitliskajam piemēram normālvienādojuma sistēma bija sastādīta  12.2.4. paragrafā. Tās koeficientu matrica ir

                                   .      

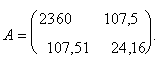 Ja sistēma tika atrisināta ar inversās matricas palīdzību, tad kā starprezultāts bija jāfiksē šī matrica:

                                  .       

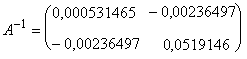             Inversās matricas atrašana, īpaši ja tā ir liela, jāveic, izmantojot lielu zīmīgo ciparu skaitu. Izdarāmās darbības ir tādas, ka to rezulttātā bieži samazinās  zīmīgo ciparu skaits, kas ved pie skaitļošanas kļūdu uzkrāšanās..

            Tālāk koriģējam neizskaidroto dispersiju:

 

                         

            Līdz ar to ir  visi sākotnējie dati regresijas koeficientu standartkļūdu aprēķināšanai ar formulu (12.34):

 

 

            Regresijas koeficientu standartkļūdas izmanto attiecīgo robežkļūdu un vērtējumu robežu aprēķināšanai. Robežkļūdu atrod, standartkļūdu pareizinot ar t koeficientu, kas atbilst attiecīgajam brīvības pakāpju skaitam un izvēlētai varbūtībai. Piemērā mums ir  n - m - k = 40 - 2 - 2  = 36  brīvības pakāpes. Ja izvēlamies intervāla drošības varbūtību  0,95, tad  t  koeficients pēc Stjudenta tabulām ir  2,028.  

Līdz ar to                     

 

 

 

 

 

 

            Regresijas koeficientu vērtējumu robežas atrod no pašiem koeficientiem atskaitot un tiem pieskaitot robežkļūdas.

 

 

            Ar varbūtību  0,95  var apgalvot, ka ģenerālkopā, no kuras ir ņemta izlase, tīrumu kvalitātes nosacīti tīrā papildus ietekme uz  graudaugu ražību nav mazāka par  0,401  cnt/ha uz vienu balli un nav lielāka par 0,695  cnt/ha uz vienu balli. Tāpat minerālmēslojuma papildus ietekme nav mazāka par  4,72  un lielāka par  7,62 cnt uz   1  cnt  mēslojumu tīrvielās, rēķinot abus rādītājus uz  1  ha.

 

 

12.4.2. Svarīgāko nulles hipotēžu pārbaude

 

            Nulles hipotēzi par regresijas koeficientu var pārbaudīt, aprēķinot empīrisko  t  attiecību                                                                                                

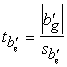                                                                   (12.35)

un to salīdzinot ar  t  - sadalījuma kritisko robežvērtību, ņemot vērā vajadzīgo varbūtību  un  n - m -k  brīvības pakāpes.

 

            Piemēram:

                                                                                                               

                               

                                                                                                                     

 

            Ja saglabājam iepriekš lietoto varbūtību  0,95,  tad pie n - m - k  = 36      

brīvības pakāpēm  t  =  2,028.  Abas empīriskās   t  attiecības ievērojami pārsniedz šo robežvērtību. Tātad nulles hipotēzes par abiem regresijas koeficientiem var noraidīt ar varbūtību, kas ir ievērojami augstāka par 0,95. Abi pētītie faktori šajās sakarībās ir statistiski nozīmīgi.

            Nulles hipotēzi par daudzfaktoru korelācijas koeficientu lietderīgi pārbaudīt,izmantojot  F  kritēriju. To parasti dara tad, ja pietiek pārbaudīt visa vienādojuma statistisko nozīmību. Mazāk atbildīgos uzdevumos tā var rīkoties, ja nav aprēķināta normālvienādojumu sistēmas koeficientu inversā matrica. Tādā gadījumā grūti izskaitļot regresijas koeficientu standartkļūdas. Ja turpretī nulles hipotēzes par regresijas koeficientiem ir pārbaudīts un vismaz viens no tiem ir statistiski nozīmīgs, tad statistiski nozīmīgs būs arī daudzfaktoru korelācijas koeficients.. Tādēļ tā nozīmību var arī nepārbaudīt.

 

 

 

 

 

 

            Daudzfaktoru korelācijas koeficienta empīrisko  F attiecību aprēķina ar formulu

 

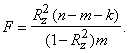                                                    (12.36)

 

Piemēram:       

 

            Ja izmantojam agrāk lietoto varbūtību   0,95,  tad kritiskā  F robežvērtība pie          un       brīvības pakāpēm ir 3,3. Empīriskā  F  attiecība tālu pārsniedz kritisko. Tādēļ nulles hipotēzi par daudzfaktoru korelācijas koeficientu var noraidīt ar varbūtību, kas ir daudz augstāka par  0,95.  Pētītās sakarības kopumā ir statistiski nozīmīgas.