7.
Lielā skaita likums un teorētiskie sadalījumi
7.1.
Lielā skaita likums
7.1.1.
Loģiski statistiskā un matemātiskā
interpretācija
Lielā skaita likums speciālajā
literatūrā ir aprakstīts no dažādiem aspektiem un
dažādās interpretācijās. Var izšķirt
loģiski statistisko un matemātisko interpretāciju.
No loģiski statistiskā
viedokļa lielā skaita likums ir vispārējs
princips, saskaņā ar kuru veidojas masveida objektu un
parādību īpašības, tādas, kuras nav
novērojamas atsevišķām šo objektu un
parādību vienībām.
Piemēram, katrā valstī, katrā
laika periodā ir raksturīgs iedzīvotāju vidējais
mūža ilgums. Latvijā 1994.g. jaundzimušā
paredzamais mūža ilgums bija vīriešiem 60,72 gadi,
sievietēm 72,87, vidēji 66,38 gadi. Šis
rādītājs mainās, mainoties vispārējam tautas
dzīves līmenim, veselības aprūpei u.c. Bet neko
tādu mēs nevaram novērot pie atsevišķa
cilvēka. Atsevišķa cilvēka mūža ilgums var
svārstīties no 0 gadiem līdz vairāk nekā 100
gadiem, un nekādas tiešas saites ar tautas vidējo
mūža ilgumu nav novērojamas.
Katra atsevišķa cilvēka
mūža ilgumu noska individuāli ģenētiski,
medicīniski un sociāli faktori.
Saskaņā ar lielā skaita likumu,
aplūkojot šos individus lielā kopumā, piemēram,
visā tautā, individuālo faktoru iedarbība
savstarpēji kompensējas jeb dzēšas.
Saglabājas galveno, visu kopumu ietekmējošo faktoru
darbība, kas formē masveida objektu un parādību
īpašības. Tās atspoguļo statistiskie
rādītāji.
Individuālo faktoru darbības
savstarpēja kompensēšanās jeb
dzēšanās, tādejādi ļaujot atklāties
masveida objekta pamatīpašībām, ir lielā skaita
likuma loģiski statistikā satura pamats.
Ar lielā skaita likuma matemātisko
interpretāciju (saturu) saprot virkni matemātisku teorēmu,
uz kurām balstās varbūtību teorija, izlases metode un,
tiešāk vai netiešāk, - citas statistikas nodaļas.
Starp šīm teorēmām nozīmīgas ir t.s.
robežteorēmas.
7.1.2.
Lielā skaita likuma robežteorēmas
Vecākā un viena no
nozīmīgākajām robežteorēmām ir Bernulli
teorēma. Tā apgalvo, ka pastāvot zināmiem
nosacījumiem, relatīvais biežums ![]() tiecas uz
varbūtību p, ja neierobežoti palielina novērojumu
skaitu. Uz šīs robežteorēmas balstās
varbūtības statistiskā definīcija.
tiecas uz
varbūtību p, ja neierobežoti palielina novērojumu
skaitu. Uz šīs robežteorēmas balstās
varbūtības statistiskā definīcija.
Ar matemātisku izteiksmi Bernulli
robežteorēmu pieraksta šādi:
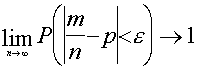 . (7.1)
. (7.1)
Vārdos šī teorēma skan diezgan
smagi: Ja katrā no n neatkarīgiem novērojumiem
gadījuma A notikšanas varbūtība p (mazais) ir
nemainīga, tad, neierobežoti palielinot novērojumu skaitu n,
var panākt, lai varbūtība P (lielais), ka relatīvais
biežums ![]() neatšķiras
no varbūtības p vairāk par brīvi
izvēlētu, pēc patikas mazu lielumu e, ir pēc patikas tuvu
vienam.
neatšķiras
no varbūtības p vairāk par brīvi
izvēlētu, pēc patikas mazu lielumu e, ir pēc patikas tuvu
vienam.
Otra robežteorēma ir Čebiševa
teorēma. Tā pierāda, ka līdzīgos
apstākļos aritmētiskais vidējais neierobežoti
tuvojas matemātiskai cerībai.
Saprotamāka ir Čebiševa teorēma
speciālam gadījumam, to interpretējot no izlases metodes
viedokļa.
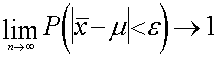 , (7.2)
, (7.2)
kur ![]() - izlases vidējais,
- izlases vidējais,
m -
ģenerālās kopas vidējais.
Vārdos:
Neierobežoti palielinot izlases vienību skaitu n, var panākt,
lai izlases un ģenerālkopas vidējo starpība
būtu pēc patikas mazs skaitlis. Par šī apgalvojuma
pareizību varam būt droši ar varbūtību, kas ir
pēc patikas tuvu vienam.
Vārds "pēc patikas" jāsaprot
tā, ka varbūtība P var būt arvien tuvāka vienam,
ja kopas vienību skaits būs arvien lielāks (tuvāks
bezgalībai).
7.1.3.
Gadījumlieluma vērtēšana, nezinot tā
sadalījumu. Čebiševa nevienādība
Izdarot gadījumlieluma vērtēšanu
(atrodot varbūtību tam atrasties prasītā
intervālā, vai intervāla robežas, kas atbilst
prasītai varbūtībai), parasti pieņem, ka
gadījumlielumam ir normāls sadalījums. Var
būt gadījumi, ka šādam pieņēmumam nav
pamata, vai pat tieši ir zināms, ka sadalījums neatbilst
normālā sadalījuma likumam.
Ja jāizdara gadījuma lieluma
vērtēšana, neko nezinot par tā sadalījumu, var
izmantot Čebiševa nevienādību.
Pierakstot ar matemātisku izteiksmi, Čebiševa
nevienādība ir šāda:
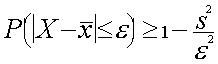 , (7.3)
, (7.3)
kur simboliem ![]() , s², e parastās
nozīmes, tikai ar e nesaprot
pēc patikas mazu, bet brīvi izvēlētu skaitli.
, s², e parastās
nozīmes, tikai ar e nesaprot
pēc patikas mazu, bet brīvi izvēlētu skaitli.
Vārdos: Varbūtība, ka gadījuma
lieluma x novirze no aritmētiskā vidējā ![]() pēc
abssolūtās vērtības nepārsniedz brīvi
izvēlētu skaitli, ir lielāka par skaitli
nevienādības labajā pusē. Pēdējo
aprēķina, atņemot no viena daļskaitli, kuras
skaitītājā ir gadījuma lieluma dispersija s², bet
saucējā - pieļaujamās kļūdas kvadrāts e². Pēdējo
nosaka, vadoties no profesionāliem apsvērumiem.
pēc
abssolūtās vērtības nepārsniedz brīvi
izvēlētu skaitli, ir lielāka par skaitli
nevienādības labajā pusē. Pēdējo
aprēķina, atņemot no viena daļskaitli, kuras
skaitītājā ir gadījuma lieluma dispersija s², bet
saucējā - pieļaujamās kļūdas kvadrāts e². Pēdējo
nosaka, vadoties no profesionāliem apsvērumiem.
Piemērs.
Strādnieku grupā, kura izpilda vienu darbu, vidējais darba
ražīgums ir 100 izstrādājumi maiņā,
rēķinot uz vienu strādnieku, ar standartnovirzi 5
izstrādājumi. Aprēķināt varbūtību,
ka kārtējā novērotā strādnieka
izstrāde nenovirzīsies no vidējās vairāk
kā par 10 izstrādājumiem. Citiem vārdiem, cik procentu
strādnieku pēc darba ražīguma iekļausies
intervālā 90-110 izstrādājumi ? Strādnieku
sadalījums pēc darba ražīguma nav zināms.
Analīze un
atrisinājums. Tāda satura uzdevumus parasti risina ar
normālā sadalījuma palīdzību, pieņemot, ka
reālais sadalījums ir tuvs normālajam. Šoreiz
uzdevumā ir atruna, ka sadalījuma raksturs nav zināms.
Tādēļ uzdevums jārisina ar Čebiševa
nevienādību.
No uzdevuma izriet, ![]() = 100; s = 5, s² = 5² = 25, e = Dx = 10
(pieļaujamā absolūtā kļūda). Tie visi ir
vajadzīgie lielumi, kas jāievieto Čebiševa
nevienādībā.
= 100; s = 5, s² = 5² = 25, e = Dx = 10
(pieļaujamā absolūtā kļūda). Tie visi ir
vajadzīgie lielumi, kas jāievieto Čebiševa
nevienādībā.
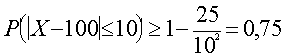 .
.
Secinājums. Varbūtība, ka
konkrēta strādnieka izstrāde nenovirzīsies no
vidējās izstrādes vairāk nekā par 10
izstrādājumiem ir lielāka par 0,75.
Secinājuma alternatīva redakcija.
Pieļauto novirzi 10 pieskaitot un atskaitot no vidējā, varam
izveidot intervālu, kura varbūtību meklējam, un
tā robežas:
x1 = 100 - 10 = 90,
x2 = 100 + 10 = 110,
90 < X > 110
un atrisinājumu
pierakstīt šādi:
P (90 < X < 110) > 0,75.
Varbūtība, ka
kārtējā strādnieka izstrāde nebūs
mazāka par 90 un lielāka par 110, nav mazāka par 0,75. No
tā var secināt, ka vismaz 75% strādnieku pēc darba ražīguma
iekļausies šajā intervālā.
Var rasties jautājums, kāpēc
Čebiševa nevienādību nelieto vienmēr, risinot
šāda tipa uzdevumus, jo vajadzīgie izskaitļojumi ir
vienkāršāki nekā izmantojot normālā
sadalījuma likumu ? Turklāt risinājuma drošība nav
saistīta ar papildus nosacījumiem par sadalījuma raksturu.
Lai pārliecinātos, kā iegūtos
secinājumus ietekmē informācija par sadalījuma
raksturu, atrisināsim iepriekšējo uzdevumu, papildus nosakot,
ka strādnieku sadalījums pēc darba ražīguma ir
normāls.
Tad uzdevums ir atrisināms kā
normālā sadalījuma tiešais uzdevums.
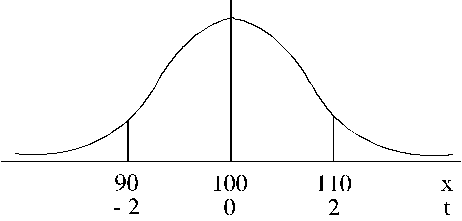
7.1. attēls.
Normālā sadalījuma uzdevuma ilustrācija.
![]() ,
,
![]() ,
,
![]() .
.
Salīdzinot iegūto rezultātu ar to, ko
aprēķinājām ar Čebiševa
nevienādību, atrodam divas būtiskas priekšrocības.
1. Atrisinājums ar normālā
sadalījuma likumu dod konkrētu ar prasīto intervālu
saistītu varbūtību 0,95, kamēr Čebiševa
nevienādība deva tikai šīs varbūtības
vērtējuma zemāko robežu 0,75.
2. Tā kā skaitlis 0,75 varbūtību
skalā ir daudz mazāks par 0,95, tad normālā
sadalījuma likums dod daudz lielāku drošību par to, ko
dod Čebiševa nevienādība.
Tajā pat laikā jāievēro, ka
atrisinājumi nav pretrunīgi. Čebiševa
nevienādība apgalvoja, ka varbūtība nav mazāka
par 0,75, resp. ir vienāda vai lielāka par šo skaitli. 0,95 ir
lielāks par 0,75, tātad formāli nav pretrunā ar
Čebiševa teorēmas apgalvojumu. Tikai Čebiševa
nevienādība dod mazāk un nekonkrētāku
informāciju.
Vēl noskaidrosim, ar kādu
varbūtību varētu saistīt iepriekšējā
uzdevumā prasīto intervālu, ja papildus noteiktu, ka
strādnieku sadalījums pēc darba ražīguma nav vis
normāls, bet vienmērīgs. Tas gan ir tīri formāls
pieņemums, jo reāli vienmēr būs vairāk
strādnieku ar vidējam tuvu darba ražību, bet maz - ar
ļoti lielu vai ļoti mazu darba ražību.
Vienmērīga sadalījuma grafiks ir
taisnstūris x ar robežvērtībām a, b.
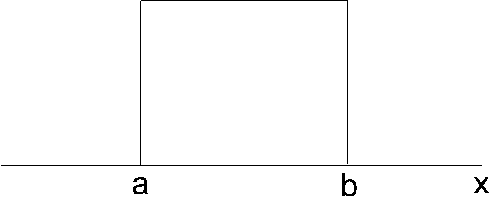
7.2. attēls.
Vienmērīga sadalījuma ilustrācija.
Lai atrisinātu
uzdevumu, ir jāatrod, kur uz skaitļu ass x attiecībā
pret a un b atrodas uzdevumā dotās robežvērtības
90 un 100. To varēs izdarīt, ja būs aprēķinātas
a un b skaitliskās vērtības. To izdarām, zinot
vienmērīga sadalījuma dotos parametrus ![]() = 100 un s = 5 un iesaistot viņus šo parametru
aprēķināšanas formulās:
= 100 un s = 5 un iesaistot viņus šo parametru
aprēķināšanas formulās:
![]() , (7.4)
, (7.4)
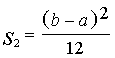 . (7.5)
. (7.5)
Izdarot aizvietojumus un
izteiksmes vienkāršojot, iegūstam:
![]() ;
a + b = 200.
;
a + b = 200.
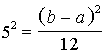 , no kurienes b - a
=17,32.
, no kurienes b - a
=17,32.
Līdz ar to a un b
vērtības varam iegūt, atrisinot sistēmu:
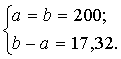
To izdarot, iegūstam,
ka a = 91,34; b= 108,66 (kuri atrodas vienādos attālumos no ![]() =100).
=100).
Uzskatāmības
dēļ visus èetrus punktus (x1 = 90, x2
= 110, a = 91, b = 109) atliekam kopējā grafikā (7.3.
attēls).
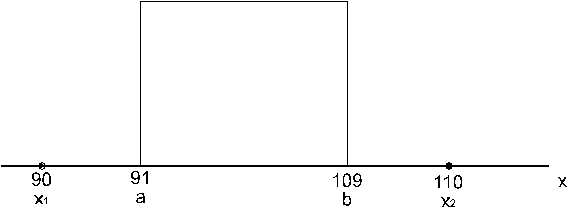
7.3. attēls.
Atrisinājuma ilustrācija.
Redzam, ka viss
teorētiskais sadalījums atrodas starp uzdevumā
prasītajiem punktiem 90 un 110.
Tātad pie hipotēzes, ka strādnieku
sadalījums ir vienmērīgs, nevar būt strādnieku
ar darba ražīgumu zemāku par 90 un augstāku par 110.
Par to, ka kārtējā strādnieka darba
ražīgums atradīsies šajā intervālā
varam būt droši ar vaarbūtību 1:
![]()
Arī tas nav pretrunā ar Čebiševa
nevienādību, jo 1 > 0,75.
7.2.
Normālā un logaritmiski normālā sadalījuma
aprēķināšana
7.2.1.
Normālā sadalījuma aprēķināšana
Variācijas rindā, ja tā ir izveidota
pēc izlases vai citādi ierobežotas kopas datiem,
biežumi no grupas uz grupu neizmainās laideni, plūstoši,
bet ar dažādām atkāpēm no sadalījuma
likumsakarības. Var pieņemt, ka sadalījuma pamatraksturu
nosaka pētījamā statistiskā objekta būtiskas
īpašības, bet dažādas novirzes no šī
pamatrakstura - nejaušu, gadījuma faktoru darbība.
Pēdējā ir jo manāmāka, jo mazāka ir
apstrādājamo datu kopa.
Variācijas rindas novirzes no sadalījuma
pamatrakstura līdz ar to var vērtēt kā izlases
kļūdas.
Lai atbrīvotos no šīm izlases
kļūdām, variācijas rinda, ko sauksim par empīrisko
sadalījumu, ir jāizlīdzina ar kādu laidenu līkni,
citiem vārdiem, empīriskais sadalījums ir
jāaizstāj ar teorētisko.
Ja empīriskais sadalījums ir saistīts
ar konkrētu izlasi, tad teorētiskais sadalījums ir
atbilstošās ģenerālās vai
hipotētiskās kopas vērtējums. Tādejādi
teorētiskā sadalījuma aprēķināšana
no izlases teorijas viedokļa nozīmē izlases
empīriskā sadalījuma izplatīšanu uz
ģenerālkopu.
Atrastais teorētiskais sadalījums dod
iespēju izdarīt interpolāciju novērotā izlases
variācijas apgabala ietvaros: precizēt interesējošo
intervālu absolūtos un relatīvos biežumus,
atbrīvojoties no izlases kļūdām,
aprēķināt biežumus pēc vajadzības
šaurākos un plašākos intervālos. Teorētiskais
sadalījums dod arī iespēju izdarīt
ekstrapolāciju ārpus izlases variācijas apgabala, nosakot,
kādi varētu būt biežumi intervālos, kuri
izlasē ir palikušsi tukši, ja tālāk
palielinātu izlases lielumu, resp. vienību skaitu tajā.
Lai aprēķinātu zinātniski
pamatotu teorētisko sadalījumu, ir jābūt
šādai informācijai:
1. Zinātniskai teorijai vai vismaz hipotēzei
par statistiskā objekta būtiskām
īpašībām, kuras nosaka sadalījuma
vispārējo raksturu. Tas dod iespēju izdarīt
izvēli starp dažādām teorētisko
sadalījumu funkcijām (modeļiem), kādus
piedāvā varbūtību teorija un matemātiskā
statistika. Statistikas teorijā un praksē visbiežāk un
plašāk izmanto normālo sadalījumu un logaritmiski
normālo sadalījumu. Tos aplūkosim plašāk,
mēģinot noskaidrot viņu piemērotību
konkrētajam pētījumu objektam;
2. Ir jābūt iepriekš
aprēķinātiem izraudzītā sadalījuma
parametriem, kuri vispārīgam teorētiskam sadalījumam
piešķir konkrētas īpašības. Normālo
sadalījumu nosaka divi tā parametri: aritmētiskais
vidējais (vispārinot - matemātiskā cerība) un
standartnovirze.
7.1. tabula
Mājsaimniecību
sadalījums pēc gada kopienākuma, rēķinot uz
vienu mājsaimniecības locekli un normālā un
logaritmiski normālā sadalījuma biežumi
|
Kopienākums |
Intervāla |
Mājsaimniecību |
Normālais |
Logaritmiski
normālais |
||
|
gadā Ls |
centrs x |
skaits faktiski |
sadalījums |
sadalījums (lg) |
||
|
|
x |
f |
f1 |
f - f1 |
f2 |
f - f2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 - 200 |
100 |
- |
7,0 |
-7,0 |
0,1 |
-0,1 |
|
200 - 400 |
300 |
10 |
9,4 |
0,6 |
7,5 |
2,5 |
|
400 - 600 |
500 |
26 |
16,6 |
9,4 |
26,7 |
-0,7 |
|
600 - 800 |
700 |
29 |
24,8 |
4,2 |
37,3 |
-8,3 |
|
800 - 1000 |
900 |
37 |
31,0 |
6,0 |
35,3 |
1,7 |
|
1000 - 1200 |
1100 |
22 |
32,7 |
-10,7 |
27,9 |
-5,9 |
|
1200 - 1400 |
1300 |
30 |
28,9 |
1,1 |
20,2 |
9,8 |
|
1400 - 1600 |
1500 |
14 |
21,5 |
-7,5 |
13,9 |
0,1 |
|
1600 - 1800 |
1700 |
14 |
13,4 |
0,6 |
9,3 |
4,7 |
|
1800 - 2000 |
1900 |
6 |
7,1 |
-1,1 |
6,2 |
-0,2 |
|
2000 - 2200 |
2100 |
5 |
3,1 |
1,9 |
4,1 |
0,9 |
|
2200 - 2400 |
2300 |
4 |
1,2 |
2,8 |
2,7 |
1,3 |
|
2400 - 2600 |
2500 |
- |
0,4 |
-0,4 |
1,8 |
-1,8 |
|
2600 - 3000 |
... |
- |
0,1 |
-0,1 |
2,0 |
-2,0 |
|
3000 - 6000 |
... |
- |
|
|
1,8 |
-1,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Kopā |
- |
197 |
197,2»197 |
-0,2»0 |
196,8 |
0,2»0 |
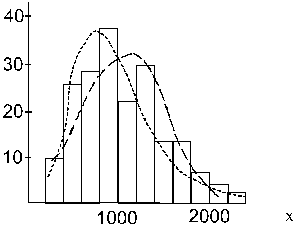
7.4. attēls.
Empīriskā sadalījuma izlīdzināšana ar
normālo un logaritmiski normālo sadalījumu.
_ _ _ _ normālais sadalījums,
------ logaritmiski normālais
sadalījums.
Izstrādājamā teorētiskā
sadalījuma parametri ir jāaprēķina pēc izlases
vai cita rakstura reāli novērotas statistikas kopas datiem. Nav
obligāti, lai abi parametri būtu aprēķināti no
vienas un tās pašas kopas datiem.
Statistikas praksē datu apstrāde parasti ir
organizēta tā, ka vienmēr tiek
aprēķināti novēroto pazīmju
aritmētiskie vidējie un relatīvie biežumi. Tajā
pat laikā ļoti reti aprēķina variācijas
rādītājus. Tādēļ, aprēķinot
teorētisko sadalījumu, ir iespējams izmantot
aritmētisko vidējo, kurš ir
noteikts vai nu pēc ģenerālkopas vai citādas
plašas statistikas kopas datiem. Turpretim standartnovirze bieži ir
jāaprēķina pēc daudz mazākas izlases datiem,
bet atsevišķos gadījumos jānovērtē
ekspertīzes ceļā.
Teiktais nenozīmē, ka visus vajadzīgos
parametrus nevarētu aprēķināt pēc vienas un
tās pašas izlases datiem. Tas pat ir vēlams, īpaši
tad, ja izdarītā izlases nav maza. Tā rīkosimies
turpmāk.
7.1. tabulas pirmajās trīs ailēs un
7.4. attēlā ar histogrammu ir parādīts
vēsturiskais 1936/37.g. izlases mājsaimniecību
sadalījums pēc gada kopienākuma, rēķinot uz
vienu patērētāja vienību. Tā kā
stabiņi histogrammā neveido pakāpeniski augošu un
pēc tam dilstošu piramīdveida figūru, ir pamats šo
histogrammu izlīdzināt ar kādu teorētisku
sadalījumu. Sākumam izvēlēsimies normālo
sadalījumu.
Normālo sadalījumu parasti
aprēķina vai nu ar datoru vai vismaz programmētas
vadības kalkulātoru, tādēļ izskaitļojumus
parādīsim tikai vienam intervālam.
Lai sāktu aprēķināt
normālā sadalījuma biežumus, ir jāzina
sadalījuma aritmētiskais vidējais un standartnovirze.
Apstrādājot 7.1. tabulas datus, par variantiem pieņemot
intervālu centrus, iegūstam, ka ![]() = 1059,39 un s =
476,00. Kopas vienību skaits n
= 197.
= 1059,39 un s =
476,00. Kopas vienību skaits n
= 197.
Aprēķinot normālā
sadalījuma biežumus, parasti izvēlas tādas pašas
intervālu robežas kā empīriskajā
sadalījumā, jo tas atvieglo abu sadalījumu salīdzināšanu
piemēram ar Hī kvadrāta kritēriju. Tomēr tas
nav obligāti. Tabulas lejasdaļā esam izveidojuši divus
plašākus intervālus, kuros nav biežumi empīriskajā,
bet varētu būt biežumi teorētiskajā
sadalījumā.
Normālā sadalījuma
aprēķināšana būtībā
neatšķiras no normālā sadalījuma tiešajiem
uzdevumiem, tikai varbūtība (biežumi) jāaprēķina
nevis dažiem, bet samērā daudziem intervāliem, lai
varētu uzzīmēt normālā sadalījuma
līkni.
Kā piemēru aprēķināsim
normālā sadalījuma biežumu 3.intervālā,
kura zemākā robeža xz = 400 un
augstākā (augšējā) robeža za =
600. Ir jāizpilda šādas darbības.
1. Abas kritiskās robežas
jāstandartizē:
![]()
![]()
2. Matemātiskajās tabulās jāatrod
vai jāizskaitļo šīm vērtībām
atbilstošās normālā sadalījuma F(t) funkcijas un to
starpība.
F(ta = -0,96) = 0,1685;
F(tz = -1,38) = 0,0838.
Varbūtība kārtējai
mājsaimniecībai nonākt 3.intervālā ir 0,1685 -
0,0838 = 0,0847. Tas ir arī normālā sadalījuma
biežums viena daļās.
3. Lai iegūtu normālā sadalījuma
biežumu šajā intervālā, kas atbilstu
empīriskā sadalījuma biežumam, biežumu viena
daļās jāpareizina ar n = 197.
n3(norm.) = 0,0847 × 197 = 16,7
(mājsaimniecības).
Šis skaitlis, izskaitļots ar programmu (ar
lielāku starprezultātu precizitāti) 16,6 ir ierakstīts
7.1. tabulas 4. ailes 3. rindā.
Pārējos normālā sadalījma
biežumus izskaitļo analogi. Ja izmanto neprogrammējamu
skaitļošanas tehniku, aprēķinus lietderīgi
sakārtot darba tabulā.
Darbu beidzot, jāpārbauda, vai
teorētisko biežumu summa, neskaitot noapaļošanas
kļūdas, atbilst empīrisko biežumu summai.
Normālo sadalījumu iezīmē
attēlā, atliekot tajā punktus, kuru koordinātes atbilst
intervālu centriem un normālā sadalījuma
biežumiem. Pēc tam tos savieno ar laidenu līkni. Ja grib
uzzīmēt precīzāku līkni, jāņem
vairāk un šaurāki intervāli normālajā
sadalījumā.
7.4. attēlā redzam, ka normālā
sadalījuma līkne empīriskā sadalījuma histogrammu
izlīdzina diezgan tuvināti.
7.2.2.
Logaritmiski normālā sadalījuma
aprēķināšana
Sociāli ekonomiskajā statistikā ir
bieži jāsastopas ar sadalījumiem, kuriem ir raksturīga
pozitīva asimetrija: sadalījuma labais zars ir vairāk vai
mazāk izstiepts, bet kreisais - aprauts. Tādu sadalījumu
bieži veido iedzīvotāju sadalījums pēc
ienākumiem un līdz ar to arī pēc galvenajām
izdevumu grupām.
Minimālo ienākumu nereti reglamentē
likumdošanas ceļā likumi par minimālo darba algu, par
minimālo pensiju utt. Maksimāli pieļaujamie ienākumi
tādā veidā reglamentēti netiek. Arī
reālā cilvēka izdzīvošana ir saistīta ar
zināmu minimālu ienākumu. Tie ir tiesiski - materiālie
priekšnoteikumi, lai iedzīvotāju sadalījums pēc
ienākumiem un izdevumiem būtu ar pozitīvu asimetriju.
Normālais sadalījums, kā zināms,
ir simetrisks pret aritmētisko vidējo. Tādēļ
minētajos un līdzīgos gadījumos tas nevar būt
pietiekami labs empīrisko sadalījumu matemātiskais modelis,
jo neatklāj vienu būtisku empīriskā sadalījuma
īpatnību. Šādos gadījumos samērā
bieži ar labām sekmēm var izmantot logaritmiski
normālo sadalījumu.
Kopas vienību sadalījums ir logaritmiski
normāls, ja normālo sadalījumu veido nevis paši
sākotnējie dati (grupētu datu gadījumā -
intervālu vidējie vai to centri), bet viņu logaritmi.
Skaitļu logaritmi vienmēr ir daudz
mazāki nekā paši skaitļi. Turklāt mazu skaitļu
un viņu logaritmu starpība nav tik liela kā lielu
skaitļu un viņu logaritmu starpība. Pārejot no
skaitļu skalas uz logaritmu skalu, viss variācijas apgabals tiek
"saspiests", taèu nevienmērīgi. Lielo
skaitļu apgabalā, sadalījuma labajā zarā, skalas
"saspiešana" ir daudz intensīvāka.
Tādēļ, ja sadalījums sākotnējo datu
skalā ir ar izteiktu pozitīvo asimetriju, pārceļot
viņu logaritmiskajā skalā, zināmos
apstākļos tas kļūst simetrisks.
Ja pēc datu logaritmēšanas
empīriskais sadalījums kļūst tuvs normālam, par
sākotnējā sadalījuma matemātisku modeli var
noderēt logaritmiski normālais sadalījums.
Logaritmiski normālo sadalījumu
aprēķina līdzīgi kā normālo
sadalījumu, ,tikai visos galvenajos darba posmos dati ir
jālogaritmē.
Kā teorētiskā sadalījuma
parametri datu aritmētiskā vidējā un standartnovirzes
vietā ir jāņem datu logaritmu aritmētiskais
vidējais un datu logaritmu standartnovirze. Logaritmu bāzei nav
būtiskas nozīmes. Strādājot ar skaitļotāju,
bieži izmanto naturālos logaritmus, bet, strādājot ar
tabulām, ērtāki ir decimāllogaritmi.
Logaritmu vidējo un standartnovirzi var
rēķināt trejādi.
Ja datus apstrādā ar skaitļotāju
un izmanto iepriekš nesagrupētus datus, visprecīzākos
rezultātus var iegūt, logaritmējot katra
atsevišķa novērojuma datus un iegūtajiem logaritmiem
rēķinot aritmētisko vidējo un standartnovirzi ar
parastajām formulām
Ja apstrādā grupētus datus
(viendimensijas variācijas rindu), logaritmē grupu vidējos
vai intervālu centrus un no iegūtajiem logaritmiem izskaitļo
svērto aritmētisko vidējo un svērto
standartnovirzi. Par statistiskajiem svariem izmanto vienību skaitu
katrā grupā (intervālā).
Ja arī sākotnējo datu variācijas
rinda nav pieejama, bet ir zināms interesējošās
pazīmes aritmētiskais vidējais un standartnovirze, no
pēdējiem var tuvināti izrēķināt
logaritmu vidējo un logaritmu standartnovirzi, izmantojot
speciālas redukcijas formulas (decimāllogaritmiem):
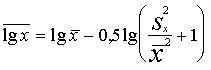 ; (7.6)
; (7.6)
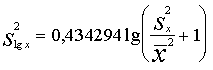 . (7.7)
. (7.7)
Par to, kurš no pēdējiem diviem
paņēmieniem dod precīzākus rezultātus,
literatūrā nav īstas vienprātības.
Pēc mūsu ekspertīzes
vērtējuma, ja datu aritmētiskais vidējais un
standartnovirze arī ir aprēķināti pēc
grupētiem nevis nesagrupētiem datiem un pēc tā
paša grupējuma, ar to pašu intervālu skaitu
rēķina logaritmu vidējo un logaritmu standartnovirzi,
precīzāks varētu būt otrais paņēmiens,
un to lietosim turpmāk.
Ja turpretim datu vidējais un standartnovirze ir
aprēķināti precīzāk pēc
nesagrupētiem datiem vai izvērsta grupējuma ar daudziem
intervāliem, bet logaritmu vidējo un logaritmu standartnovirzi
grib rēķināt pēc vienkāršota
grupējuma ar nedaudz intervāliem, šis paņēmiens
var neattaisnoties. Tad precīzākus rezultātus, zināmos
apstākļos var dot redukcijas formulas (7.6.-7.7.), kuru
izmantošana ir daudz vienkāršāka.
Tā ka logaritmiski normālais sadalījums
kā jebkurš modelis interesējošo objektu apraksta tikai
tuvināti, no prakses viedokļa parasti nav būtiskas
nozīmes, vai logaritmu vidējais un logaritmu standartnovirze ir
aprēķināti ar lielāku vai mazāku
precizitāti, ja vien tie nav būtiski kļūdaini.
Logaritmiski normālo sadalījumu parasti
vispirms aprēķina tādiem pat intervāliem, kādi
izmantoti empīriskajā sadalījumā. Intervālu
robežas standartizē ar formulu
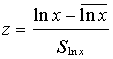 .
.
Ja sākotnējo skaitļu skalā
izmantoti vienāda lieluma intervāli, kā to parasti dara
praksē, tad logaritmu skalā intervāli kļūst
nevienādi. Šaurāki intervāli veidojas pazīmes lielo
vērtību apgabalā (labajā zarā), bet
plašāki - mazo vērtību apgabalā (kreisajā
zarā). Tādēļ ir vērojams, ka logaritmiski
normālais sadalījums labāk izlīdzina
empīriskā sadalījuma labo zaru, bet nereti sliktāk -
kreiso zaru.
Parādīsim ar piemēru logaritmiski
normālā sadalījuma aprēķināšanu
vienam intervālam. Iepriekš pēc 7.1. tabulas datiem ir
aprēķināts, ka ![]() , slgx=0,2122. Izmantosim vēlreiz
trešā intervāla robežās xz = 400; xa
= 600.
, slgx=0,2122. Izmantosim vēlreiz
trešā intervāla robežās xz = 400; xa
= 600.
1. Kritisko
robežu logaritmu standartizēšana:
![]() ;
;
![]() .
.
2. Atbilstošo F(t)
un to starpības atrašana:
F(-1,77) =
0,0384;
F(-0,94) =
0,1736;
F(ta)
- F(tz) = 0,1736 - 0,0384 = 0,1352.
3.
Atbilstošā logaritmiski normālā sadalījuma
biežuma atrašana:
0,1352 × 197 = 26,6.
Pēdējais, izskaitļojot ar programmu
26,7 ir ierakstīts 7.1. tabulas 6.ailē līdz ar citiem
logaritmiski normālā sadalījuma biežumiem. Logaritmiski
normālais sadalījums 7.4. attēlā ir
iezīmēts ar punktētu līniju. Kā jau bija
sagaidāms, tas empīrisko sadalījumu labāk
izlīdzina tā labajā zarā, sliktāk -
kreisajā, mazo x vērtību apgabalā.
7.2.3.
Izlīdzināšanas kvalitātes novērtēšana
ar Hī kvadrāta kritēriju
Ar Hī - kvadrāta kritēriju
salīdzina savā starpā divus sadalījumus un
noskaidro, vai tie atšķiras statistiski nozīmīgi, vai
nē. Visbiežāk salīdzina empīrisko sadalījumu
ar teorētisko, noskaidrojot, vai teorētiskais
sadalījums ir labs empīriskā sadalījuma modelis, vai
nē. Citos gadījumos salīdzina savā starpā divus
empīriskos sadalījumus, īpaši tad, ja tie veidoti pēc
atributīvas pazīmes. Pēdējā
gadījumā parastie variācijas, asimetrijas un citi
rādītāji nav aprēķināmi. Hī -
kvadrāta metode ir tehniski vienkārši realizējama, nav
darbietilpīga.
Hī - kvadrāta metodei ir raksturīga parastā
hipotēzes pārbaudes shēma: aprēķina
empīrisko rādītāju, šajā gadījumā
Hī kvadrātu un to salīdzina ar tabulu robežvērtību.
Atkarībā no tā, kurš skaitlis lielāks,
pieņem lēmumu.
Empīrisko skaitli Hī kvadrāts
aprēķina ar formulu
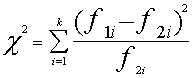 , (7.8)
, (7.8)
kur f1 un f2
ir salīdzināmo sadalījuma rindu biežumi
atbilstošajos intervālos (ar Nr. i). Summēšana notiek pa
visiem intervāliem.
Lielumam Hī - kvadrāts ir
absolūtā skaitļa īpašības. Ja
atsevišķi daļskaitļi
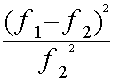
nav nulles, tad summa
parasti būs lielāka, ja saskaitāmo ir vairāk.
Jāievēro, kurus biežumus ņemt
par f1 un kurus par f2, jo formulā šie
lielumi nav simetriski. Ja salīdzina empīrisko sadalījumu ar
teorētisko, par f2 jāņem teorētiskā sadalījuma
biežumi. Salīdzinot eksperimenta rezultātus ar
kontroles rezultātiem, par f2
jāņem kontroles rezultāti. Salīdzinot divus
empīriskos sadalījumus, f2 (saucējā)
aprēķina pēc speciālas metodikas.
Izmantojot Hī kvadrāta kritēriju,
empīrisko sadalījumu var salīdzināt ar jebkuru
teorētisko sadalījumu: normālo, logaritmiski normālo,
binomiālo u.c.
Lai novērtētu empīriskā
sadalījuma atbilstību teorētiskam sadalījumam,
pieņemot, ka tas jau aprēķināts, ir jāizdara
šādas darbības:
1. jāaprēķina
empīriskais Hī kvadrāts c²;
2. jānoteic brīvības
pakāpju skaits n;
3. jāatrod atbilstošais tabulas
kritērijs vai empīriskā c² varbūtība un
jāizdara
vajadzīgais secinājums.
Empīriskais Hī kvadrāts ir summa. Lai
kāds saskaitāmais tajā nekļūtu
nesamērīgi liels, jāseko, lai biežumi visās
grupās, īpaši teorētiskajā sadalījumā,
būtu pietiekami lieli skaitļi, vismaz lielāki par 5. Ja tas
tā nav, daži intervāli ir jāapvieno. Hī
kvadrāta kritērijs mazāk reaģē uz
intervālu apvienošanu nekā uz iespēju , ka kāds f2i formulas (7.8)
saucējā ir mazs skaitlis. Tādēļ pirms
empīriskā Hī kvadrāta izskaitļôšanas
apvienojam 7.1. tabulā pirmos divus intervālus, iegūstot
"0-400 latu" un visus pēdējos intervālus,
iegūstot "vairāk nekā 2000 latu".
Tad empīrisko Hī kvadrātu
normālajam sadalījumam var izskaitļot šādi
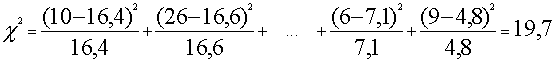 .
.
Summā tik
saskaitāmo, cik salīdzināmo grupu; izskaitļošanu
ieteicams izdarīt ar nelielu programmu.
Salīdzinot empīrisko sadalījumu ar
logaritmiski normālo sadalījumu, iegūstam c²=12,0. Brīvības
pakāpju skaitu nosaka, atskaitot no salīdzināmo grupu
(intervālu) skaita k savstarpēji neatkarīgo nosacījumu
skaitu l, kas izriet no uzdevuma nosacījumiem, kā arī
parametru skaitu, kas izmantots aprēķinot teorētisko
sadalījumu, m:
n = k - l - m.
Pēc intervālu apvienošanas tiek
salīdzinātas 10 grupas, tātad k = 10. Lineāro
nosacījumu skaits ir viens - absolūto biežumu summai
jābūt 197, tātad l = 1. aprēķinot
normālo sadalījumu, tika izmantoti divi no izlases
sadalījuma ņemti parametri ![]() un s². Tātad m = 2. Līdz ar to
brīvības pakāpju skaits ir šāds:
un s². Tātad m = 2. Līdz ar to
brīvības pakāpju skaits ir šāds:
n = l0 - 1 - 2 =
7.
Darba noslēdzošajā posmā
jāaizvēlas varbūtība resp. nozīmības
līmenis, ar kuru pārbauda hipotēzi par
eempīriskāa un teorētiskā sadalījuma atbilstību.
Izmantojam klasisko varbūtību 0,95 (a = 0,05). Tad
speciālās Hī kvadrāta kritisko robežu
tabulās var nolasīt skaitli, kuru empīriskajam Hī
kvadrātam pārsniedzot, hipotēze par abu sadalījumu
atbilstību ir jānoraida.
Atrodam, ka
![]() .
.
Empīriskais Hī - kvadrāts
normālam sadalījumam bija 79,7, tātad hipotēze par
sadalījumu atbilstību ir jānoraida. Logaritmiski
normālajam sadalījumam empīriskais Hī kvadrāts bija
12,0, t.i. mazāks par kritisko robežu. Tātad logaritmiski
normālo sadalījumu varam uzlūkot par apmierinošu
dotā empīriskā sadalījuma modeli.
Hī kvadrāta kritēriju plaši lieto
arī dažādu citu statistikas hipotēžu
pārbaudei, t.sk. neparametriskās statistikas metodēs.
Izmantojot Hī kvadrāta kritēriju,
jāievēro šādi galvenie nosacījumi:
1. kopējam empīriskā
sadalījuma vienību skaitam jābūt pietiekami lielam,
vismaz
n > 50;
2.
biežumiem visos sadalījumu intervālos jābūt
pietiekami lieliem, ne mazākiem kā
5 - 10;
3.
absolūto biežumu vietā nedrīkst ņemt
relatīvos biežumus procentos vai viena
daļās;
4.
secinājumi, pamatojoties uz šo kritēriju nedrīkst
būt kategoriski, jo grupu skaits
empīriskajā
sadalījumā ir noteikts ekspertīzes ceļā.