9.3. Vienkāršas lineārās regresijas vienādojums
9.3.1. Modelis un tā parametru aprēķināšana
Aplūkojot grupējuma attēlā empīriskas regresijas
līniju, redzam, ka tā atspoguļo noteiktu sakarību: kā faktorālās pazīmes
izmaiņu rezultātā izmainās rezultatīvā pazīme. Bet šai sakarībai uzslāņojas
dažādu blakus faktoru darbības rezultāti. Attēlā tie parādās kā tādi vai citādi
līnijas lauzumi vai pat "zāģa zobi". Var pieņemt, ka sakarību
vispārējo raksturu, atbrīvotu no šo nejaušību radītās ietekmes, izteiktu taisne
vai līkne, kura atrastos maksimāli tuvu visām empīriskās regresijas līnijas
virsotnēm. Tādu taisni vai līkni, pretstatā empīriskai, sauc par teorētisko
regresiju.
Teorētisko regresiju vienkāršoti var iegūt
vizuāli izlīdzinot empīrisko. Tomēr tādā veidā var iegūt tikai tuvinātus
rezultātus. Precīzus rezultātus iegūst, aprēķinot matemātiski izlīdzinošās
taisnes vai līknes vienādojumu.
Teorētisko regresiju tuvināti var aprēķināt pēc
analītiskā grupējuma, jo abas metodes risina vienu un to pašu loģiski
statistisko uzdevumu. Tomēr tā parasti nedara, jo grupēšanas rezultātā ir
zudusi liela daļa derīgās iznformācijas, īpaši rezultatīvās pazīmes iekšgrupu
variācija. Tādēļ teorētisko regresijas vienādojumu un arī sakarību ciešuma
rādītājus parasti aprēķina pēc sākotnējiem, nesagrupētiem datiem.
Risināmā uzdevuma nostādni, nesaistot to ar
grupēšanu, var labāk izprast, izgatavojot un aplūkojot korelācijas diagrammu.
Izgatavojot korelācijas diagrammu, tāpat kā izgatavojot analītiskā grupējuma
attēlu, uz abscisu ass atliek faktorālās, bet uz ordinātu ass - rezultatīvās
pazīmes skalu. Pašā attēlā ar punktiem iezīmē visas kopas vienības (katrai savs
punkts) atbilstoši faktiskajiem datiem par divām saistītajām pazīmēm.
Ja pastāv ciešas sakarības, visi punkti grupējas
ap kādu iedomātu taisni vai līkni (kura vēlāk būs jāaprēķina). Ja sakarības ir
vidēji ciešas, vairums punktu koncentrējas iedomātā elipsveida figūrā. Ja
sakarību nav, punkti korelācijas diagrammā ir izvietoti haotiski, ja ap tiem
mēģina apvilkt iedomātu figūru, iegūst apli. Tad tālākie aprēķini nesola
pozitīvus rezultātus.
Teorētiskās regresijas vienādojumu var uzlūkot
par ekonometrisku modeli, kurš, vadoties no noteikta mērķa un atbilstoši
noteiktam kritērijam, vislabāk modelē mūs interesējošās sakarības. Tādēļ tāpat
kā jebkurā modelēšanas procesā vispirms ir loģiski un profesionāli jāpamato
modeļa vispārējais veids. Konkrētā gadījumā ir jāpamato, vai interesējošās
sakarības var modelēt ar lineāru vienādojumu vai jāizmanto nelineārs; ja tā,
tad kāds. Šo darba jomu sauc par sakarību formas izvēli.
Sakarību modeļa formu izvēlas un pamato ar vienu
vai vairākiem paņēmieniem, no kuriem minēsim divus.
Izdarot loģiski profesionālus spriedumus.
Piemēram, lineāra sakarību forma būs pamatota tad, ja var pieņemt, ka
faktorālās pazīmes izmaiņām visumā atbilst rezultatīvās pazīmes aritmētiski
proporcionālas izmaiņas.
Izgatavojot un novērtējot korelācijas diagrammu.
Ja vairums punktu attēlā grupējas ap iedomātu taisni, ir pamats lietot lināru
modeli (vienādojumu). Plašāk par šiem jautājumiem rakstīts nākošajā nodaļā.
Ja, aplūkojot korelācijas diagrammu, par
pieņemamu var uzlūkot visvienkāršāko, lineāro sakarību formu, modeli
vispārējā veidā var pierakstīt šādi:
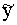 =a+bx, (9.1)
=a+bx, (9.1)
kur y - rezultatīvā
pazīme,
x - faktorālā pazīme,
a, b - modeļa
parametri, kuru skaitliskās vērtības jāaprēķina.
Plašākos pētījumos, kad vienā darbā jāaplūko
vairāki modeļi ar dažādām rezultatīvām un faktorālām pazīmēm, tās kodē ar
skaitļiem. Tad iepriekšējo modeli var pierakstīt, piemēram, šādi:
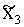 =a+bx5 . (9.2)
=a+bx5 . (9.2)
Šis modelis nav matemātiska funkcija parastā
izpratnē, jo kā parāda grupējumi un individuālie dati, sakarības nav
funkcionālas.
Nepilnīgu (daļēju) sakarību gadījumā gan dabā,
gan sabiedrībā šo sakarību raksturs parasti ir korelatīvs.
Sakarību starp divām pazīmēm sauc par korelatīvu,
ja faktorālās pazīmes izmaiņas ir saistītas ar rezultatīvās pazīmes vidējo
vērtību izmaiņām. Zinot x, viennozīmīgi nevar noteikt (prognozēt) kāds būs y.
Bet, ņemot atbilstoši dažādām x vērtībām vai to intervāliem novērojumu
apakškopas (grupas) un rēķinot grupu vidējās rezultatīvās pazīmes vērtības, tās
pakļaujas noteiktai likumsakarībai - proti ir vairāk vai mazāk precīzi
nosakāmas ar meklējamo modeli.
Ja modeli (9.1) grib pierakstīt kā
funkciju, tajā ir jāparāda arī t. s. nejaušību komponents (citu faktoru
darbības rezultāts e).
Tad 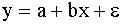 . (9.3)
. (9.3)
Tā kā e
var noteikt kā y un 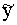 starpību tikai darba
noslēguma posmā, par modeli uzlūko izteiksmi (9.1), bet, lai akcentētu minēto
īpatnību, uz rezultatīvās pazīmes simbola liek vilnīti (citi autori - jumtiņu
^).
starpību tikai darba
noslēguma posmā, par modeli uzlūko izteiksmi (9.1), bet, lai akcentētu minēto
īpatnību, uz rezultatīvās pazīmes simbola liek vilnīti (citi autori - jumtiņu
^).
Kad modeļa (9.1) vispārējais veids ir pamatots,
ir jāaprēķina tā parametru skaitliskās vērtības. Modeli (9.1) statistikā un
ekonometrijā sauc par vienkāršu (pāru) lineāru regresijas
vienādojumu, tā koeficientu b par regresijas koeficientu,
bet
a - par vienādojuma brīvo locekli.
Lai modelis kļūtu konkrēts un atspoguļotu
interesējošas sakarības, ir jānosaka, izmantojot satistiskos datus, parametru a
un b vērtības. To, principā, var izdarīt ar vairākām metodēm. Statistikā un
ekonometrijā visplašāko pielietojumu ir guvusi vismazāko kvadrātu metode.
Saskaņā ar to a un b jāaprēķina tā, lai noviržu kvadrātu summa faktiski
novērotām un ar modeli (9.1) aprēķinātām rezultatīvās pazīmes vērtībām būtu
minimāla.
Matemātiskā pierakstā:
Qz=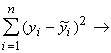 min. (9.4)
min. (9.4)
Matemātiskajā statistikā pierāda, ka šīm
prasībām atbilst taisne, kuras parametri a un b ir aprēķināti sastādot un
atrisinot t. s. normālvienādojumu sistēmu:
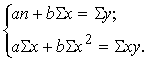 (9.5)
(9.5)
Sistēmu (9.5) var atrisināt vispārīgā veidā,
iegūstot ērtas formulas regresijas koeficienta un brīvā locekļa aprēķināšanai:
b=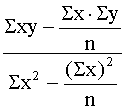 , (9.6)
, (9.6)
a=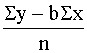 , vai a=
, vai a=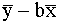 . (9.7)
. (9.7)
Formulās (9.6) un (9.7) ievietojamās summas
jāaprēķina pēc savāktajiem statistiskajiem datiem īpašā darba tabulā. Ja darbu
izpilda ar programmētās vadības datoru, šāda tabula nav jāsastāda. Tā veidojas
mašīnas atmiņā.
9.3.2. Regresijas skaitliska ilustrācija
Turpmākām ilustrācijām izmantosim piemēru no
iedzīvotāju dzīves līmeņa pētījumiem. Viegli iedomāties,ka iedzīvotāju naudas
izdevumus, piemēram, pārtikas iegādei, nosaka, no vienas puses, vajadzība,
piemērā, ēstgriba, bet, no otras puses, maksātspēja, kuru savukārt nosaka mājsaimniecības
ienākumi.
Tādēļ, lai pētītu, kā izmainās iedzīvotāju
izdevumi pārtikas produktu iegādei y, mainoties mājsaimniecības ienākumiem x,
ir jāizmanto modelis:
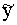 =f(x), kurš atspoguļos korelatīvas sakarības. Tiklab
ienākumi, kā pārtikas izdevumi jāaprēķina uz 1 mājsaimniecības locekli,
precīzāk - uz 1 patērētāja vienību vai nu gadā vai mēnesī. Šādus datus dod
mājsaimniecības budžetu statistika, un tos ievāc Centrālā statistikas pārvalde.
=f(x), kurš atspoguļos korelatīvas sakarības. Tiklab
ienākumi, kā pārtikas izdevumi jāaprēķina uz 1 mājsaimniecības locekli,
precīzāk - uz 1 patērētāja vienību vai nu gadā vai mēnesī. Šādus datus dod
mājsaimniecības budžetu statistika, un tos ievāc Centrālā statistikas pārvalde.
9.5. tabula
Darba tabula sākotnējās informācijas
sagatavošanai, lai aprēķinātu mājsaimniecību pārtikas
izdevumu lineāru modeli pēc naudas ienākumiem, izmantojot 20 mājsaimniecību
budžetu datus, Ls mēnesī, rēķinot uz 1 mājsaimniecības locekli.
|
Ģimenes
|
Sākotnējie dati
|
Aprēķinātie lielumi
|
Novērtēšanas lielumi
|
|
Nr.
|
Naudas ienākums
|
Izdevumi pārtikai
|
|
|
|
|
|
|
i
|
x
|
y
|
x²
|
y²
|
x
y
|
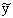
|
y - 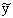
|
|
1.
|
32.17
|
13.84
|
1035
|
191.6
|
445.2
|
14.3
|
-0.46
|
|
2.
|
178.65
|
48.88
|
31916
|
2389
|
8732
|
49.18
|
-0.3
|
|
3.
|
12.15
|
6.31
|
147.6
|
39.82
|
76.67
|
9.54
|
-3.23
|
|
4.
|
73.65
|
25.15
|
5424
|
632.5
|
1852
|
24.18
|
0.97
|
|
5.
|
43.95
|
16.88
|
1932
|
284.9
|
741.9
|
17.11
|
-0.23
|
|
6.
|
100.1
|
32.13
|
10020
|
1032
|
3216
|
30.48
|
1.65
|
|
7.
|
15.42
|
8.37
|
237.8
|
70.06
|
129.1
|
10.32
|
-1.95
|
|
8.
|
78.72
|
27.53
|
6197
|
757.9
|
2167
|
25.38
|
2.15
|
|
9.
|
143
|
40.82
|
20449
|
1666
|
5837
|
40.69
|
0.13
|
|
10.
|
59.77
|
10.45
|
3572
|
109.2
|
624.6
|
20.88
|
-10.43
|
|
11.
|
160.5
|
44.74
|
25760
|
2002
|
7181
|
44.86
|
-0.12
|
|
12.
|
21.05
|
10.31
|
443.1
|
106.3
|
217
|
11.66
|
-1.35
|
|
13.
|
90.08
|
29.87
|
8114
|
892.2
|
2691
|
28.09
|
1.78
|
|
14.
|
122.55
|
36.21
|
15019
|
1311
|
4438
|
35.82
|
0.39
|
|
15.
|
200.3
|
52.55
|
40120
|
2762
|
10526
|
54.34
|
-1.79
|
|
16.
|
51.27
|
19.81
|
2629
|
392.4
|
1016
|
18.85
|
0.96
|
|
17.
|
79.84
|
21.05
|
6374
|
443.1
|
1681
|
25.65
|
-4.6
|
|
18.
|
171.12
|
40.41
|
29282
|
1633
|
6915
|
47.39
|
-6.98
|
|
19.
|
110.55
|
49.76
|
1221
|
2476
|
5501
|
32.97
|
16.79
|
|
20.
|
30.21
|
20.44
|
912.6
|
417.8
|
617.5
|
13.84
|
6.6
|
|
Kopā
|
1775.05
|
555.51
|
221806
|
19609
|
64604
|
555.5
|
-0.02
|
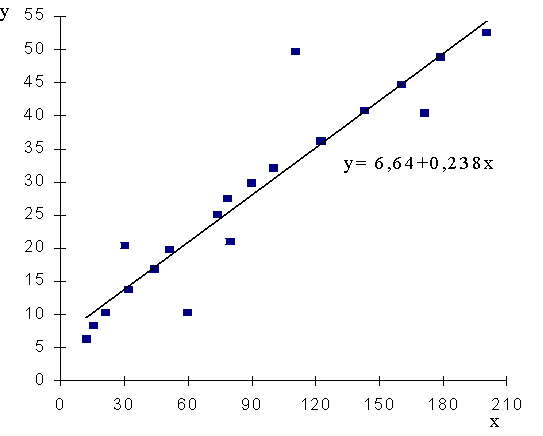
9.3.
attēls. Korelācijas diagramma un regresijas taisne : iedzīvotāju naudas
ienākumi x
un izdevumi
pārtikas iegādei y, rēķinot uz 1 mājsaimniecības locekli
mēnesī, Ls.
9.5. tabulā ir parādīts neliels fragments no
šiem datiem un tie ir attēloti korelācijas diagrammā 9.3. attēlā.
Iedzīvotāju dzīves līmeņa pētījumi ir
pierādījuši, ka šādas t.s. pārtikas izdevumu funkcijas ir nelineāras. Tām ir
jāatspoguļo patēriņa piesātinājuma efekts. Tomēr, ja sākotnējo datu ir maz, to
variācijas apgabals nav liels, sakarību nelinearitāte var izpausties vāji. Tad
nelineāra modeļa vietā var izmantot lineāru kā vienkāršāku.
Šajā vietā mēs arī aprēķināsim vienkāršāko
lineāro modeli, lai vēlāk citā vietā runātu arī par nelineāriem.
Tātad kārtējais uzdevums ir pēc 9.5. tabulas
datiem aprēķināt lineāra modeļa 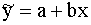 , parametrus a un b,
kur
, parametrus a un b,
kur
x - iedzīvotāju naudas ienākumi mēnesī,
y - izdevumi pārtikas produktu iegādei mēnesī,
abus rēķinot vidēji uz vienu mājsaimniecības
locekli, latos.
Sākotnējā informācija ir parādīta 5. tabulas 1.
- 3. ailēs. Ja strādā ar taustiņu skaitļotāju (kalkulatoru) ir jāaipilda 4. -
6. ailes, kuru kopsummmas kopā ar 2. - 3. aiļu summām var ievietot darba
formulās (9.6) un (9.7).
Kā svarīgākais
regresijas vienādojuma parametrs ir koeficients b. Tādēļ to aprēķina pirmo :
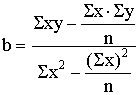 =
=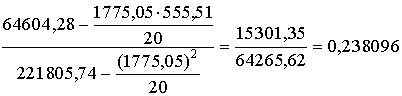 .
.
Skaitļi formulā jāievieto, noapaļojot līdz
vienādam zīmīgo ciparu skaitam, piemēram, līdz sešiem, atbildē atstāj vienu
zīmīgo ciparu mazāk.
Regresijas koeficienta ekonometrisko un
ģeometrisko interpretāciju aplūkosim turpmāk.
Līdzīgi aprēķina vienādojuma brīvo locekli.
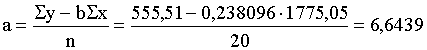 .
.
Tātad meklētais regresijas vienādojums ir:
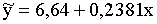 .
.
Lai izdarītu aprēķinu loģisko pārbaudi, atrastam
vienādojumam atbilstošo taisni iezīmē korelācijas diagrammā. Šim nolūkam atrod
divus punktus, kas atrodas uz taisnes. Punktu abscisas izvēlas brīvi, bet
ordinātas atrod, izvēlētās abscisu vērtības ievietojot vienādojumā. Kad punkti
atlikti korelācijas diagrammā, caur tiem novelk taisni.
Ja regresijas vienādojums aprēķināts pareizi,
atzīmēm korelācijas diagrammā jāsadalās tā, lai apmēram puse no atzīmēm atrodas
vienā un puse - otrā pusē no taisnes. Ja taisne atzīmes korelācijas diagrammā
nedala tieši uz pusēm, tad tajā pusē, kurā atzīmju skaits mazāks, to attālumam
no taisnes jābūt lielākam.
Cik labi lineārs regresijas vienādojums modelē
interesējošās sakarības, var vērtēt pēc atzīmju (punktu) sadalījuma abpus
taisnei dažādās korelācijas diagrammas daļās.
Mūsu 9.3 attēlā centrālajā daļā vairums punktu
atrodas virs regresijas taisnes, bet labajā zarā - zem tās. Tādēļ punktu
izvietojumu korelācijas diagrammā precīzāk attēlotu līkne, kura attēla
centrālajā daļā atrastos nedaudz virs taisnes, bet abās malās - zem tās. Tādas
īpašības būtu pakāpes funkcijai, kuru arī plaši izmanto iedzīvotāju dzīves
līmeņa pētījumos.
Tomēr jāņem vērā, ka neviens modelis precīzi
neatspoguļo īstenību, bet tikai tuvināti. Arī pakāpes funkcija mūs interesējošo
sakarību aprakstītu tikai kā vispārēju tendenci. Tādēļ nebūs pareizi teikt, ka
lineārs modelis šīs sakarības atspoguļo nepareizi.
Dažādi modeļi ir jāvērtē tā, ka viens no tiem precīzāk, otrs
tuvinātāk atspoguļo īstenību. Precīzāku modeli izvēlas tad, ja
ir pietiekoši daudz sākotnējās informācijas, lai precīzākā modeļa priekšrocības
būtu statistiski nozīmīgas. Ja informācijas ir maz un tā pēc sava
rakstura ir ļoti aptuvena, ir pamats izvēlēties vienkāršāko modeli.
Piemēriem, kuri bija parādīti 9.1. - 9.3.
tabulās un 9.1. - 9.2. attēlos, un pētī barības atdevi piena lopkopībā,
atbilstošie pāru sakarību regresijas vienādojumi ir šādi:
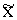 0=71,6x1+3239; r01=0,245;
0=71,6x1+3239; r01=0,245;
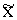 0=99,9x2+2323; r02=0,698, kur
0=99,9x2+2323; r02=0,698, kur
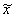 0 - vidējais izslaukums no govs gadā, kg;
0 - vidējais izslaukums no govs gadā, kg;
x1 - siena
patēriņš simtos barības vienību (saka arī "centneros barības
vienību") vidēji uz govi gadā;
x2 -
spēkbarības patēriņš simtos barības vienību vidēji uz govi gadā.
9.3.3. Regresijas parametru interpretācija
Regresijas koeficients b izsaka
rezultatīvās pazīmes papildus pieaugumu Dy, kurš ir
saistīts ar faktorālās pazīmes pieaugumu par vienu vienību, tas ir Dx=1. Iepriekšējā
pārtikas izdevumu modelī b = 0,24. No tā var secināt, ka dotajos apstākļos,
palielinoties iedzīvotāju naudas ienākumiem par 1 latu (rēķinot uz 1 mājsaimniecības
locekli mēnesī), viņi pārtikas produktu iegādei papildus izdod Ls 0,24 jeb 24
santīmus. Tāds izdevumu pieaugums ir jāvērtē kā vidējais visu mājsaimniecību
kopā. Atsevišķās mājsaimniecībās tas būs gan mazāks gan lielāks, jo papildus
naudas ienākumus dažādas mājsaimniecības izlieto dažādi, vadoties no mājsaimniecības
sastāva, dzīvokļa apstākļiem, veselības stāvokļa, ģimenes tradīcijām, interesēm
utt. Tādēļ izpētītā un modelētā sakarība "ienākumi - izdevumi pārtikas
iegādei" nav funkcionāla, bet korelatīva.
Par korelatīvu sauc sakarību, ja mainoties faktorālās
pazīmes vērtībām, likumsakarīgi izmainās rezultatīvās pazīmes vidējie lielumi.
Citā terminoloģijā - rezultatīvās pazīmes grupu vidējie, ja grupējums ir
izdarīts pēc faktorālās pazīmes.
Sekojot ekonomterijas un arī mikroekonomikas
teorijai, saka, ka regresijas koeficients rāda pētītā faktora papildus
rezultātu. Piemērā tie ir papildus izdevumi pārtikai.
Papildus rezultāts ir jāatšķir no vidējā
rezultāta. Piemērā - no vidējiem izdevumiem pārtikas iegādei, kuri visā
novērojumu kopā ir vienādi ar pārtikas izdevumu īpatsvaru mājsaimniecību
budžetos. Pēdējo aprēķina, dalot rezultatīvās pazīmes datu summu ar faktorālās
pazīmes datu summu.
No 9.5. tabulas summu rindas iegūstam, ka 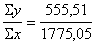 =0,313»31
(santīmi).
=0,313»31
(santīmi).
Ekonometrijas modeļos papildus rezultāts parasti
ir mazāks nekā vidējais rezultāts. No loģikas viedokļa to izskaidro t.s.
piesātinājuma efekts. No formālā viedokļa - pozitīvs brīvais loceklis lineārā
regresijas vienādojumā.
Ģeometriski regresijas koeficients
ir regresijas taisnes un abscisu ass veidotā leņķa a tangenss.
|
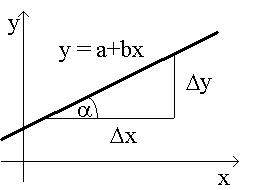
9.4. attēls. Regresijas koeficienta
ģeometriska
interpretācija.
|
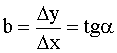 . (9.8)
. (9.8)
Ļoti
svarīgi ievērot, ka leņķa a
tangenss ir jāaprēķina kā pieaugumu Dy
un Dx
attiecība, pēdējos nolasot atbilstoši izvēlētajām x un y
skalām. Leņķi var nolasīt ar leņķmēru un tā tangensu atrast trigonometriskās
tabulās tikai tad, ja uz abām koordinātu asīm ir atliktas pazīmes vienās
vienībās, piemēram, latos, un arī mērogi izraudzīti vienādi. Statistikas praksē
to ievēro reti, tādēļ leņķmēru šādam nolūkam lietot nedrīkst.
Regresijas vienādojuma brīvo locekli dažkārt
interpretē kā rezultatīvās pazīmes vidējo (teorētisko) vērtību ar nosacījumu,
ka faktorālās pazīmes vērtība ir 0.
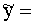 a+b(x=0)=a.
a+b(x=0)=a.
Tāda interpretācija ir pieļaujama tikai
atsevišķos gadījumos. Vispār no tās vajag atturēties. Par to var
pārliecināties, praktiski rēķinot dažādus regresijas vienādojumus. Bieži
brīvais loceklis iznāk negatīvs skaitlis. Bet ekonomikā rezultatīvās pazīmes
parasti nevar būt negatīvi skaitļi (Izņēmums - peļņa, ja ciesti zaudējumi).
Šķietamā pretruna izskaidrojama ar to, ka, pilnīgi trūkstot kādam ražošanas
faktoram, ražošana parasti vispār nav iespējama. Tāpat trūkstot ienākumiem,
vispārējā gadījumā nav iespējami izdevumi. Tādēļ punktā x = 0 sakarību modelis
reāli neeksistē.
Līdz ar to ir jānosaka un jāatrunā regresijas
vienādojuma eksistences apgabals. Izmantojot statistikas metodes, to
nosaka kā dubultnevienādību, zemāko robežu ņemot kā faktorālās pazīmes mazāko
vērtību, kāda sastopama sākotnējos datos, bet augstāko robežu - kā faktorālās
pazīmes lielāko vērtību, kāda sastopama sākotnējos datos.
xmin<x<xmax
. (9.9)
Izskatot sākotnējās informācijas tabulas datus,
varam noteikt, ka atrastais regresijas vienādojums reāli eksistē apgabalā:
|
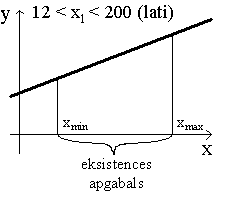
9.5. attēls. Regresijas vienādojuma
ģeometriska
interpretācija
|
Vadoties
no kvalitatīviem apsvērumiem, parasti no ekonomikas teorijas, modeļa
eksistences apgabals varētu būt plašāks. Taču, formāli paplašinot vienādojuma
eksistences apgabalu, varam pieļaut kļūdu, jo interesējošās sakarības, kas
izpētīto datu variācijas apgabalā visumā ir lineāras, ārpus šī apgabala var būt
izteikti nelineāras. Piemēram, ļoti lielu ienākumu gadījumā izdevumi pārtikai
tuvojas piesātinājumam.
Vienādojuma brīvais loceklis ģeometriski nozīmē
nogriežņa garumu uz ordinātu ass no koordinātu sākuma līdz krustpunkatam ar
regresijas taisni. Jāņem vērā algebriskā zīme, un nogriežņa garums jānolasa
ordinātu ass skalā (nevis jāmēra, piemēram, milimetros).
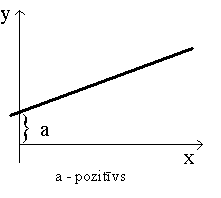
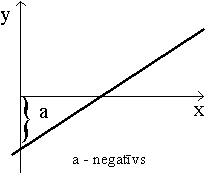
9.6.
attēls. Regresijas brīvā locekļa ģeometriska interpretācija.
Tā kā summa nav atkarīga no saskaitāmo kārtības,
regresijas vienādojumu var pierakstīt:
·
pirmo uzrādot brīvo locekli; tā pieņemts
matemātikā;
·
pirmo uzrādot reizinājumu bx, jo
regresijas koeficients ir galvenais modeļa parametrs; tā ieteicams rīkoties,
demonstrējot modeli praktiķiem.
Vēl daži aizrādījumi par korelācijas diagrammas
izgatavošanu.
Lai korelācijas diagramma un regresijas taisne
neradītu izkropļotu priekšstatu par pētītā faktora ietekmi, pareizi jāizvēlās
mērogi uz abām koordinātu asīm. Ja faktora ietekme jāvērtē kā normāla, attēlu
ieteicams izgatavot tā, lai regresijas taisne veidotu ap 25 - 300
lielu leņķi ar abscisu asi, šoreiz mērot ar parasto leņķmēru. Ja ekspertīzes
ceļā ir novērtēts, ka faktora ietekme ir liela (piemēram, salīdzinot ar
tradicionāliem normatīviem) mērogus var izvēlēies tā, lai taisne iznāk nedaudz
stāvāka (līdz 450). Ja faktora ietekme ir jānovērtē kā nepietiekama,
mērogus var pieņemt tā, lai taisne būtu tuvāka horizontālai (15 - 200).
Jāievēro, ka attēla vizuālo iespaidu veido tas leņķis,
kuru
mēra ar leņķmēru. Tas savukārt ir saistīts ar priekšnoteikumu, ka uz
abām koordinātu asīm atliktas samērojamas pazīmes vienā un tajā pašā mērogā.
Praktiski pazīmes un skalas visbiežāk ir atšķirīgas. Tādēļ visi vērtējumi un
aprēķini jāizdara vadoties no tiem.
Līdz ar to formāli pareizi pēc vieniem un tiem
pašiem datiem var izgatovot neierobežoti daudz attēlu, kuri rada pilnīgi
atšķirīgu vizuālo iespaidu. Šādos nenoteiktības apstākļos ir apzināti jāizlemj,
kādu iespaidu grib radīt un atbilstoši tam jāizveido skalas uz koordinātu asīm.
Piemēram, ir jāattēlo regresijas vienādojums 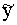 =16 + 8x. Izvēlamies uz x ass attēlot vienu vienību ar 2 cm,
(4 rūtiņas), bet uz y ass ar 1 cm attēlojam 10 vienības. Tad attēls būs šāds
(skat. 9.7. attēlu).
=16 + 8x. Izvēlamies uz x ass attēlot vienu vienību ar 2 cm,
(4 rūtiņas), bet uz y ass ar 1 cm attēlojam 10 vienības. Tad attēls būs šāds
(skat. 9.7. attēlu).
Mērot ar leņķmēru, iegūstam , ka a»240,
kam atbilst tg 240 »
0,45.
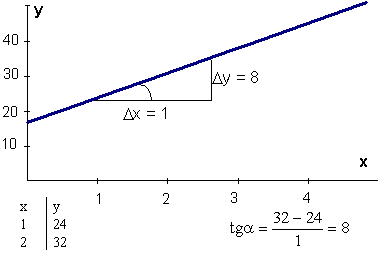
9.7. attēls. Attēls ar saspiestu vertikālo skalu.
Tagad "izstiepsim" y asi divas reizes,
apzīmējot 10 vienības ar 2 cm:
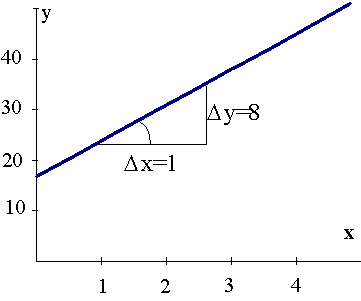
9.8. attēls. Attēls ar izstieptu vertikālo skalu.
Arī šajā gadījumā 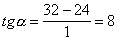 . Toties mērot ar leņķmēru šajā gadījumā a = 400
un tg 400 »
0,84.
. Toties mērot ar leņķmēru šajā gadījumā a = 400
un tg 400 »
0,84.
Abi attēli ir formāli pareizi, bet pirmais rada
vizuālu iespaidu, ka faktora ietekme ir neliela, turpretī otrs: - ka faktora
ietekme ir ļoti liela.
9.3.4. Aprēķināto jeb teorētisko lielumu
un noviržu interpretācija
Par teorētisko jeb pēc regresijas
vienādojuma aprēķināto lielumu sauc rezultatīvās pazīmes lielumu, kuru iegūst,
ievietojot regresijas vienādojumā faktorālās pazīmes simbola vietā kādu fiksētu
skaitli. Teorētiskais lielums ir rezultatīvās pazīmes vidējā, arī visvarbūtīgākā
vērtība, kas atbilst izvēlētai faktorālās pazīmes vērtībai.
Iepriekšējā piemērā aprēķinājām, ka iedzīvotāju
ienākumus x un izdevumus pārtikas iegādei y saista regresijas vienādojums:
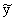 = 6,64+0,2381x.
= 6,64+0,2381x.
Sestai mājsaimniecībai 9.5. tabulā naudas
ienākums rēķinot uz vienu mājsaimniecības locekli, bija Ls 100,10. Ievietojot šo skaitli
vienādojumā, iegūstam
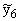 = 6,64 + 0,2381×100,1
= 30,48 (lati).
= 6,64 + 0,2381×100,1
= 30,48 (lati).
Ja šī mājsaimniecība saimniekotu atbilstoši
vidējam, kas raksturīgs šādam ienākumam, viņa pārtikai izdotu Ls 30,48 mēnesī.
Tas ir sava veida statistisks normatīvs ar ko salīdzināt faktisko rezultatīvās
pazīmes lielumu. Piemērā 6. mājsaimniecībai tas ir Ls 32,13. Novirze y - 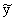 = 32,13 - 30,48 = 1,65
rāda, ka šī mājsaimniecība pārtikai ir izdevusi vairāk nekā vidēji citas
mājsaimniecības līdzīgos apstākļos.
= 32,13 - 30,48 = 1,65
rāda, ka šī mājsaimniecība pārtikai ir izdevusi vairāk nekā vidēji citas
mājsaimniecības līdzīgos apstākļos.
Plašāk nekā dzīves līmeņa pētījumos šādu
aprēķinu un tā rezultātus izmanto, vērtējot rezultātus ražošanā. Ekonometrijā
saka - ražošanas funkciju teorijā. Tādēļ otru piemēru ņemsim no ražošanas
funkcijām lauksaimniecībā.
Pēc 9.1. tabulas datiem ir aprēķināts lineārs
regresijas vienādojums, kas rāda vidējā izslaukuma y izmaiņas, mainot govīm
izbarotās spēkbarības daudzumu x.
Izsakot y kilogramos gadā vidēji no 1 govs, bet
x - centneros barības vienību, kas izbaroti vidēji govij gadā, ieguvām tuvinātu
vienādojumu :
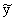 = 2323 + 100x.
= 2323 + 100x.
Mainot x mērvienību, var teikt, ka vidēji viens
kg spēkbarības dod 1 kg piena.
Vidēji saimniecību grupā 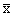 = 12,0 (cntn), bet
= 12,0 (cntn), bet 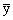 =3523 kg.
=3523 kg.
Mūs interesējošā konkrētā saimniecībā, rēķinot
uz 1 govi gadā ir izbarots 14,6 c. b. v. spēkbarības un iegūts izslaukums
vidēji no govs 3600 kg gadā (4. saimniecība 9.1. tabulā).
Jānovērtē šis saimniecības ražošanas potenciāls
piena ražošanā un tā izmantošana.
Ekonomikas analīzē plaši lieto salīdzināšanu.
Tradicionālā darbā visbiežāk salīdzina ar kopas vidējo, ar pirmrindas uzņēmumu
sasniegumiem, ar uzņēmējdarbības plāna rādītājiem, ar iepriekšējā gada
rezultātiem utt. Šādā gadījumā vai nu pilnīgi vai daļēji neņem vērā reālās
ražošanas iespējas, ražošanas faktorus.
No visiem ražošanas potenciālu veidojošiem
faktoriem pagaidām mums ir zināms tikai viens - spēkbarības devas. Spriežot pēc
šī faktora, un salīdzinot to ar vidējo, saimniecībā ražošanas potenciāls ir
lielāks nekā vidēji līdzīgu saimniecību kopā: x - 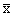 = 14,6 - 12,0 = 2,6
(c. b. v.)
= 14,6 - 12,0 = 2,6
(c. b. v.)
Arī ražošanas
rezultāts - izslaukums vidēji no govs ir lielāks nekā vidēji saimniecību kopā:
y - 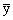 = 3600 - 3523 = 77
(kg).
= 3600 - 3523 = 77
(kg).
Tas tomēr nedod atbildi uz jautājumu, vai
ražošanas potenciāls, kas ir lielāks par vidējo, ir izmantots labāk par vidējo,
vidējā līmenī, vai sliktāk par vidējo.
Šādu atbildi var iegūt, aprēķinot ar regresijas
vienādojumu teorētisko izslaukumu, kas vidēji atbilst faktiskajām spēkbarības
devām. Ievietojam iepriekš minētajā vienādojumā x = 14,6 un iegūstam:
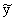 = 2323 + 100×14,6
= 3783 kg.
= 2323 + 100×14,6
= 3783 kg.
Tas ir saimniecības ražošanas potenciāls,
vērtējot ar rezultatīvo pazīmi. Faktiskais rezultāts y = 3600 ir mazāks;
novirze 3600 - 3783 = - 183 (kg).
Tātad ražošanas potenciāls, kas šajā saimniecībā
ir virs vidējā līmeņa, tomēr ir izmantots nepietiekami efektīvi. Savus šķietami
labos panākumus piena lopkopībā saimniecība ir guvusi pārtērējot dārgos
spēkbarības līdzekļus, kurus dažkārt iepērk ārpus Latvijas.
Tādējādi regresijas vienādojums kā ekonometrisks
modelis deva iespēju padziļināt saimnieciskās darbības analīzi, salīdzinot ar
tradicionāliem aprēķiniem, Reālā uzņēmuma analīzē, protams, būtu vēlams ņemt
vērā ne vienu, bet vairākus ražošanas faktorus un sakarību forma nereti jāņem
nelineāra. Tādu uzdevumu mācīšanās ir mūsu tālāks uzdevums.
Ģeometriski teorētiskais rezultatīvās pazīmes
lielums ir punkta ordināta uz regresijas taisnes, bet aplūkotā novirze y -
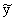 - vertikāla nogriežņa garums no novērojumam atbilstošā punkta
ordinātas korelācijas diagrammā līdz regresijas taisnei, mērot ordinātu skalā.
- vertikāla nogriežņa garums no novērojumam atbilstošā punkta
ordinātas korelācijas diagrammā līdz regresijas taisnei, mērot ordinātu skalā.
Lineāram regresijas vienādojumam ir matemātiska
īpašība, ka ievietojot tajā x = 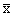 , dabūjam
, dabūjam 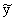 =
= 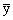 .
.
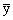 =a + b
=a + b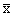 . (9.10)
. (9.10)
Pēdējā piemērā 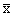 =12,0;
=12,0; 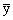 =3523. Vienādojums dod
=3523. Vienādojums dod 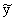 =2323 + 100×12
= 3523.
=2323 + 100×12
= 3523.
Nelielas atšķirības var rasties starprezulātu
noapaļošanas rezultātā. Ja grib iegūt precīzākas ražošanas potenciālu vērtības,
jāizmanto vienādojuma parametri un vidējie lielumi ar vairāk zīmīgiem cipariem,
pēc tam noapaļojot galīgo rezultātu. Ekonomikā daudziem zīmīgiem cipariem
parasti nav nozīmes. To ticamību nenodrošina sākotnējās informācijas nereti
diezgan zemā precizitāte.
Izsniedzot šādas un līdzīgas analīzes rezultātus
praktiķiem, viņu reakcija un uzticība materiālam lielā mērā ir atkarīga no tā,
cik saprotami un profesionāli interpretējami ir visi aprēķina starprezultāti.
Šajā ziņā izdarītajos aprēķinos vājā vieta ir
vienādojuma brīvais loceklis, kuram, kā jau minējām, profesionālā
interpretācija ir ļoti ierobežota vai tās nemaz nav. Tādēļ praktisku apsvērumu
dēļ regresijas vienādojumu ieteicams pierakstīt novirzēs no artimētiskajiem vidējiem.
Vispārējā formā tas ir:
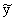 -
- 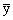 = b (x -
= b (x - 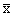 ) (9.11)
) (9.11)
jeb
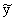 =
= 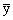 + b (x -
+ b (x - 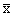 ). (9.12)
). (9.12)
Pēdējam piemēram
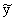 = 3524 + 100 (x - 12,0).
= 3524 + 100 (x - 12,0).
Šis vienādojums ir pilnīgi ekvivalents
iepriekšējiem un dod tos pašus teorētiskos lielumus, tikai viņš nesatur brīvo
locekli un visi aprēķinu starprezultāti ir labi saprotami.
Piemērā ievietojot x = 14,6 un fiksējot visus
starprezultātus iegūstam:
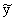 =3523+100(14,6-12,0)=3524+100×2,6=3524+260=
=3783(kg).
=3523+100(14,6-12,0)=3524+100×2,6=3524+260=
=3783(kg).
Konkrētai saimniecībai, kurā izbarots govīm
spēkbarības par 2,6 c. b. v. vairāk nekā vidēji, tā rezultātā vajadzēja iegūt
izslaukuma pieaugumu 260 kg no govs gadā. Pieskaitot to vidējam izslaukumam
visu saimniecību kopā 3524 kg, iegūstam teorētiski sagaidāmo izslaukumu
konkrētai saimniecībai 3783 kg.
Ražošanas rezultāta vērtējumus, salīdzinot ar
vidējo un ar ražošanas potenciālu var ilustrēt šādi (skat 9.9. attēlā) :
|
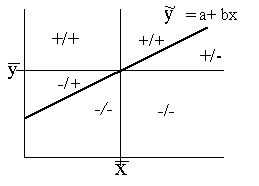
9.9. attēls. Noviržu vērtēšana
|
Vērtējuma
kvalitāti (pozitīva, negatīva) nosaka novirzes algebriskā zīme (+; -)
Vērtējuma gradāciju (apmierinoši, labi, ļoti
labi,slikti, ļoti slikti) - attiecīgās novirzes skaitliskais lielums. Jo
lielāka novirze, jo vērtējums (pozitīvs vai negatīvs) ir kategoriskāks. Kā
novērtēt novirzes lielumu, par to runāsim turpmāk.
9.3.5. Rezultatīvās un faktorālās pazīmes
attiecība (vidējais rezultāts)
Ja rezultatīvai pazīmei y un faktorālai pazīmei
x ir profesionāls (ekonomisks) saturs, tad tāds ir arī viņu attiecība y/x.
Piemērā par iedzīvotāju dzīves līmeni x bija
mājsaimniecību naudas ienākums, bet y - pārtikas izdevumi, abus rēķinot uz 1
mājsaimniecību locekli latos mēnesī. Tādā gadījumā y/x ir pārtikas izdevumi
rēķinot uz vienu latu ienākumu.
Parastā statistisko datu apstrāde dod iespēju
aprēķināt šo attiecību abu mainīgo vidējiem lielumiem 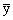 /
/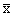 .
.
Piemērā, skat. 9.5. tabulas kopsummu rindu,
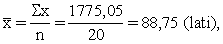
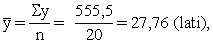
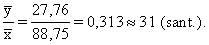
Tātad aplūkojamā mājsaimniecību izlasē no katra
ieņemtā lata mājsaimniecības vidēji izdod pārtikai 31 santīmu. Jau atzīmējām
kādēļ tas nesakrīt ar regresijas koeficientu.
Ir skaidrs, ka mājsaimniecību grupās ar dažādu
ienākumu līmeni pārtikas izdevumu daļa nebūs vienāda. Trūcīgāko mājsaimniecību
grupās šī attiecība būs lielāka un otrādi.
Tātad viens ceļš, kā noteikt šo attiecību
dažādās iedzīvotāju grupās, ir izdarīt sākotnējā materiāla grupēšanu, atrast
grupu vidējos lielumus un pēc tam šo vidējo attiecības.
Ja ir izrēķināts sakarību modelis, to pašu var
izdarīt vienkāršāk, aprēķinot rezultatīvās pazīmes teorētiskā lieluma 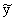 un tam atbilstošā
faktorālās pazīmes x lieluma attiecību(ekonometrijā to sauc par vidējo
rezultātu):
un tam atbilstošā
faktorālās pazīmes x lieluma attiecību(ekonometrijā to sauc par vidējo
rezultātu):
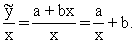 (9.13)
(9.13)
Piemērā 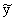 =6,64+0,2381x un
=6,64+0,2381x un 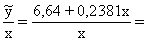
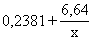 .
.
Izskaitļojam šo attiecību dažām x vērtībām
9.6. tabula
Vidējais rezultāts (pārtikas izdevumu
daļa ienākumos) pie dažādām x (ienākuma) vērtībām.
|
x
|
10
|
20
|
40
|
60
|
80
|
100
|
120
|
150
|
200
|
¥
|
|
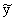 /x /x
|
0,90
|
0,57
|
0,40
|
0,35
|
0,32
|
0,30
|
0,29
|
0,28
|
0,27
|
0,24
|
Tātad, ja modelis ir pareizs, tad saskaņā ar to
vistrūcīgākā mājsaimniecību grupa, kuras mēneša ienākums vidēji uz vienu
mājsaimniecības locekli ir 10 Ls, no katra lata pārtikai izdod 90 sant. Ja
mājsaimniecības ienākums sasniedz 40 latu mēnesī, rēķinot uz 1 mājsaimniecības
locekli, no katra lata pārtikai izdod tikai 40 sant., bet, ja 100 latu - tad 30
santīmu. Vēl tālāk augot labklājībai šī daļa samazinās uz 28 - 27 santīmi,
tiecoties uz savu robežu, kas ir vienāda ar regresijas koeficientu b = 0,238 =
23,8 (sant.).
Šī iemesla dēļ dažreiz ekonometrijā saka, ka regresijas
koeficients atspoguļo faktora robežietekmi, jeb robežefektivitāti. Īpaši
plaši šādu interpretāciju lieto ražošanas funkciju teorijā, analizējot
nelineārus modeļus.
Rezultatīvās un faktorālās pazīmes konkrēto
vērtību attiecība šajā gadījumā ir lielāka par regresijas koeficientu tāpēc, ka
vienādojumā ir no nulles atšķirīgs brīvais loceklis - rezultatīvās pazīmes
lielums, kas formāli nav atkarīgs no faktorālās pazīmes lieluma. Ja a = 0, tad,
kā redzams no ilustrācijām, 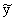 /x = b.
/x = b.
Ja kādā modelī brīvais loceklis būtu negatīvs,
tad vidējais rezultāts būtu mazāks nekā papildus rezultāts, ko atspoguļo
regresijas koeficients.
9.4. Sakarību ciešuma rādītāji
Sakarību ciešuma rādītājus, pēc interpretācijas
un lietošanas iespējām tāpat kā pazīmes variācijas rādītājus var iedalīt trīs
grupās:
1. Bāzes
rādītāji, kuriem nav reālas preofesionālas interpretācijas, bet kuriem ir
svarīga nozīme kā starprezultātiem tālākos aprēķinos. Te pieder rezultatīvās pazīmes neizskaidroto noviržu kvadrātu summa un
neizskaidrotā dispersija.
2. Absolūtie
sakarību ciešuma rādītāji, kuri ir izteikti rezultatīvās pazīmes mērvienībās. Te pieder vērtējuma pēc regresijas
vienādojuma standartkļūda un dažādas robežkļūdas.
3. Relatīvie
sakarību ciešuma rādītāji, kuri nav saistīti ar rezultatīvās pazīmes mērvienību. Svarīgākie - korelācijas un
determinācijas koeficienti. Tieši relatīvos sakarību ciešuma rādītājus praksē
lieto visplašāk. Tādēļ, ja sakarību ciešuma pētīšanai var veltīt ierobežotu
darba apjomu, ar šiem rādītājiem arī apmierinās. Tos aplūkosim pirmos.
9.4.1. Korelācijas un determinācijas koeficienti
Korelācijas koeficientu tieši pēc krossummām var
aprēķināt ar formulu:
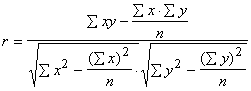 . (9.14)
. (9.14)
Lai aprēķinātu korelācijas koeficientu
iedzīvotāju pārtikas izdevumu modelim no 9.5. tabulas kopsummu rindas ir
jāizraksta formulai vajadzīgie lielumi: n=20; Sx=1775,05;
Sy=555,51; Sxy=64604,28; Sx2=221805,7;
Sy2=19609,05.
Līdz ar to
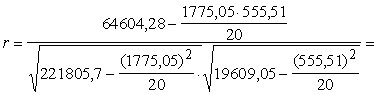
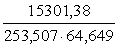
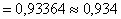 .
.
Piemēram, kas raksturoja izslaukuma atkarību no
spēkbarības patēriņa, r=0,698.
Ja r=0, tad sakarību nav nemaz. Ja r=1, tad ir
funkcionālas pozitīvas, bet ja r=-1 - funkcionālas negatīvas sakarības. Pārējos
gadījumos sakarības ir korelatīvas. Turklāt lielāks pēc absolūtās vērtības
(moduļa) koeficients norāda uz ciešākām sakarībām un otrādi.
Pieaugot sakarību ciešumam, korelācijas
koeficients neizmainās lineāri, bet palēnināti. Tā piemēram, robežās no 0,0
līdz 0,3 korelācijas koeficients norāda uz vājām, maznozīmīgām sakarībām; 0,4 -
0,7 sakarības var vērtēt kā vidēji ciešas. Un tikai tad kad r sasniedz 0,8 -
0,9, ir pieņemts uzskatīt, ka sakarības ir ciešas. Vēl tālāk pieaugot sakarību
ciešumam, nozīmīgas jau ir korelācijas koeficienta simtdaļas. Šāda korelācijas
koeficienta interpretācija gan jāvērtē kā orientējoša, jo precīzākai sakarību
ciešuma un nozīmības vērtēšanai vēl ir svarīgs kopas apjoms, pēc kāda
koeficients aprēķināts, koeficienta stabilitāte laikā u.c. Atgriežoties vēlreiz
pie korelācijas koeficienta nelinearitātes, var salīdzināt korelācijas
diagrammas, kurām atbilstošie r ir 0,2 un 0,3. Vizuāli abi attēli izskatīsies
gandrīz līdzīgi, jo punktu izvietojums maz atšķiras no haotiska. Turpretī,
salīdzinot korelācijas diagrammas, kurām atbilstošie r ir 0,92 un 0,97 būs
vērojama uzkrītoša atšķirība.
Neskatoties uz minēto šķietamo trūkumu,
korelācijas koeficients ir visbiežāk lietotais sakarību ciešuma rādītājs.
Otrs bezmērvienības (relatīvais) sakarību
ciešuma rādītājs ir determinācijas koeficients. To aprēķina kā korelācijas
koeficienta kvadrātu. Arī determinācijas koeficients var iegūt
skaitliskas vērtības no 0 līdz 1, bet tam nav algebriskās zīmes, līdz ar ko
viņš nenorāda, vai sakarības ir pozitīvas vai negatīvas.
Iepriekšējos piemēros
D=r2=(0,93364)2=0,872
un D=r2=(0,698)2=0,487.
Determinācijas koeficientu var interpretēt kā izskaidrotās
rezultatīvās pazīmes dispersijas attiecību pret kopējo (parasto)
dispersiju. Tādēļ to kā struktūras relatīvo lielumu var izteikt procentos.
Korelācijas koeficientam nav šādas īpašības, tādēļ to procentos izteikt nevar.
Tātad, pētot iedzīvotāju pārtikas izdevumu
veidošanos dotajos apstākļos, no pārtikas izdevumu visas variācijas, mērot ar
dispersiju, 87,2% izskaidro ienākumu variācija.
Pētot vidējo izslaukumu, tā variāciju dotajos
apstākļos 48,7% apmērā izskaidro govīm izbarotās spēkbarības daudzumus.
Specifisku korelācijas koeficienta
interpretāciju iegūst, ja abus korelatīvi saistītos mainīgos lielumus izsaka standartizētās
vienībās. Mainīgo standartizāciju izdara ar formulu 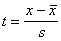 , kur s standartnovirze jeb vidējā kvadrātiskā novirze.
, kur s standartnovirze jeb vidējā kvadrātiskā novirze.
Tad korelācijas koeficientu var interpretēt
līdzīgi kā regresijas koeficientu. Ar formulu to pieraksta šādi:
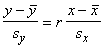 . (9.15)
. (9.15)
Korelācijas koeficients rāda, par cik
standartnovirzēm no vidējā papildus izmainās rezultatīvā pazīme, ja faktorālā
pazīme izmainās par vienu standartnovirzi no sava vidējā.
Pirmajā piemērā, pieaugot iedzīvotāju naudas
ienākumiem par vienu standartnovirzi, ir sagaidāms, ka izdevumi pārtikas
iegādei pieaugs par 0,93 standartnovirzēm.
Otrajā piemērā, palielinot spēkbarības devas
govīm par vienu standartnovirzi, ir sagaidāms, ka izslaukums papildus pieaugs
par 0,70 standartnovirzēm no sava vidējā.3
Strādājot ar programmētās vadības datoru, tajā
ievadot un apstrādājot jau standartizētus datus, regresijas un korelācijas
koeficienti tiek uzrādīti kā vienādi skaitļi.
Ņemot vērā, ka korelācijas koeficients nevar būt
lielāks par 1, rezultatīvā pazīme standartizētās vienībās nevar pieaugt
straujāk nekā faktorālā. Tā ir standartizēto datu īpatnība.
Ja abus mainīgos x un y izsaka standartizētās
vienībās un izveido koordinātu sistēmu ar šādām asīm, korelācijas koeficientu
var attēlot kā taisni, kura iet caur koordinātu sistēmas sākumu. Tā kā leņķa
koeficients pēc absolūtās vērtības vienmēr mazāks par 1, resp. -1, tad
izveidojot uz abām asīm vienāda mēroga skalas, šīs taisnes leņķis ar
horizontālo asi vienmēr mazāks par 450 (tiklab aprēķinot kā
pieaugumu attiecību, kā arī mērījot ar leņķmēru).
_____________________
3 Standartnovirze, salīdzinot ar datu
variācijas apgabalu ir liela vienība. Tādēļ šāda interpretācija ir
pieļaujama vienīgi lineāra modeļa
gadījumā, kur papildus rezultāts visā modeļa eksistences apgabalā ir
konstants.
Minēto interesanto korelācijas koeficienta
īpašibu var pierādīt, zinot, ka katra standartizētā lieluma vidējā vērtība ir
nulle, bet standartnovirze un dispersija - viens. Līdz ar to Sx=0 un Sy=0, bet Sx2=Sy2=n.
Ievietojot šos lielumus regresijas un korelācijas koeficientu formulās iegūstam
vienu un to pašu izteiksmi 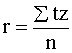 , (9.16)
, (9.16)
kur Stz
jāaprēķina standartizētiem datiem, kas atbilst sākotnējiem x, y.
Korelācijas koeficientu var apēķināt arī ar
dažādām citām formulām, kuras dod tos pašus rezultātus kā pamatformula.
Dalot formulas (9.14) skaitītāju un saucēju ar
konstantu lielumu n, iegūstam
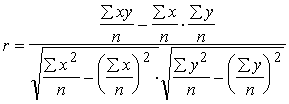 . (9.17)
. (9.17)
Pēdējās formulas saucējā saskaņā ar momentu
metodi ir abu pazīmju standartnovirzes. Skaitītāju 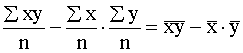 sauc par jaukto
dispersiju jeb kovariāciju un apzīmē ar simbolu covxy. Līdz ar to
korelācijas koeficientu var izteikt ar abu saistīto pazīmju kovariāciju un
standartnovirzēm:
sauc par jaukto
dispersiju jeb kovariāciju un apzīmē ar simbolu covxy. Līdz ar to
korelācijas koeficientu var izteikt ar abu saistīto pazīmju kovariāciju un
standartnovirzēm: 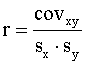 . (9.18)
. (9.18)
Tā kā
dispersija ir otrās kārtas centrālais moments, šo formulu sauc arī par korelācijas koeficienta momentu formulu.
Kovariācija tādā gadījumā ir otrās kārtas jauktais centrālais moments.
Zinot, ka dispersija ir noviržu kvadrātu summas
dalījums ar kopas vienību skaitu, reizināsim pēdējās formulas (9.18) skaitītāju
un saucēju ar n un iegūstam korelācijas koeficienta formulu, kur par sākotnējo
informāciju ir izmantotas jaukto noviržu reizinājumu un noviržu kvadrātu
summas:
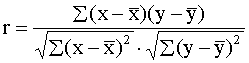 =
=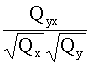 . (9.19)
. (9.19)
Formulas iegūstamas viena no otras ar
identiskiem pārveidojumiem, tādēļ tās dod vienus un tos pašus rezultātus.
Pēdējo formulu plaši izmanto matemātiskos pārveidojumos un pierādījumos.
9.7. tabula
Svarīgāko
regresijas un korelācijas rādītāju aprēķināšanas formulu sakopojums.
|
Rādītājs,
simbols
|
Summu
metode
|
Noviržu
metode
|
Momentu (dispersiju, kovariāciju) metode
|
|
Regresijas
koeficients b
|
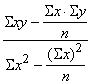
|
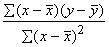
|
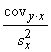
|
|
Vienādojuma brīvais loceklis a
|
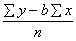
|
*****
|
*****
|
|
Korelācijas koeficients r
|
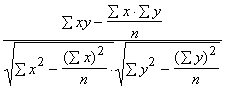
|
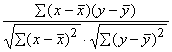
|
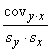
|
|
Vērtējuma standartkļūda sxy
|
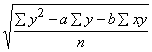
|
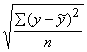
|
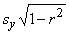
|
9.4.2 Noviržu kvadrātu summas un
dispersijas
Noviržu kvadrātu summas un dispersijas var
uzskatīt par sakarību ciešuma bāzes rādītājiem.
Bāzes sakarību ciešuma rādītājiem nav
patstāvīgas profesionālas interpretācijas un pielietojuma, bet tos izmanto kā
vērtīgus starprezultātus absolūto rādītāju aprēķināšanai, kā arī citos
aprēķinos.
Sakarību ciešuma bāzes rādītājus izveido,
sadalot sastāvdaļās rezultatīvās pazīmes noviržu kvadrātu summu un dispersiju.
Analizējot pāru sakarības, izdala izskaidroto un neizskaidroto daļu.
Matemātikā to pierāda kā dispersiju saskaitīšanas teorēmas speciālu gadījumu.
Loģisko izpratni veicina lineāro noviržu sakarību izpēte. Tādēļ izveidosim un
aplūkosim 9.6. attēlu.
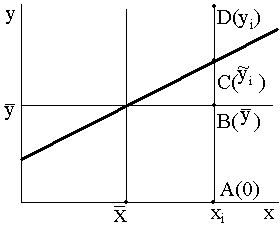
9.10.
attēls. Noviržu veidošana un kvadrātu summu sakarība.
a: AD=AB+BC+CD, kur
AD=yi=yi
AB=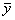
BC= -
-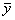
CD=y-
b: y=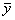 + (
+ ( -
-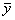 ) + (y -
) + (y - )
)
c: y-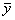 = (
= ( -
-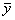 ) + (y -
) + (y - )
)
d: 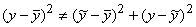
20: 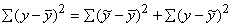
21: Q=Qf+Qz Q=å(y-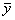 )2 Qf=å(
)2 Qf=å( -
-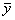 )2
)2
22: s2=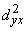 +
+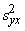 Qz=å(y-
Qz=å(y- )2
)2
Attēlā ar slīpu taisni attēlots regresijas
vienādojums 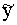 =a+bx, bet ar horizontālu rezultatīvās pazīmes vidējais
lielums y =
=a+bx, bet ar horizontālu rezultatīvās pazīmes vidējais
lielums y =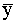 . Punkta D koordinātas xi yi atbilst
vienas kopas vienības jeb i-tā novērojuma datiem. Punkts C attēlo rezultatīvās
pazīmes teorētisko lielumu un tā ordināta ir
. Punkta D koordinātas xi yi atbilst
vienas kopas vienības jeb i-tā novērojuma datiem. Punkts C attēlo rezultatīvās
pazīmes teorētisko lielumu un tā ordināta ir 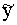 i. Punkts B attēlo rezultatīvās pazīmes
aritmētisko vidējo, un tā ordināta ir
i. Punkts B attēlo rezultatīvās pazīmes
aritmētisko vidējo, un tā ordināta ir 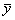 . Visu punktu abscisas ir vienādas un atbilst izvēlētai,
fiksētai faktorālās pazīmes vērtībai xi. No attēla redzams, ka
pastāv šāda nogriežņu lielumu sakarība
. Visu punktu abscisas ir vienādas un atbilst izvēlētai,
fiksētai faktorālās pazīmes vērtībai xi. No attēla redzams, ka
pastāv šāda nogriežņu lielumu sakarība
AD=AB+BC+CD.
(a)
Šo nogriežņu lielumus var izteikt algebriski un
dot tiem ekonomisku interpretāciju:
AD=yi-0=yi
raksturo rezultatīvās pazīmes faktisko lielumu
i-tai kopas vienībai;
AB=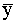 -0=
-0=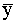
raksturo rezultatīvās pazīmes aritmētisko
vidējo;
BC=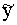 i -
i -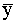
raksturo rezultatīvās pazīmes aprēķinātā jeb
teorētiskā lieluma novirzi no aritmētiskā vidējā:
CD=yi-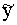 i
i
raksturo faktiskā rezultatīvās pazīmes lieluma
novirzi no teorētiskā lieluma.
Ievietojot jaunos apzīmējumus vienādībā (a), dabūjam:
yi=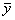 + (
+ ( i -
i -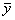 ) + (yi -
) + (yi - i). (b)
i). (b)
Tas nozīmē, ka rezultatīvās pazīmes lielumu
atsevišķi ņemtai kopas vienībai var izteikt kā trīs lielumu summu:
·
rezultatīvās pazīmes aritmētiskais
vidējais;
·
teorētiskā un aritmētiskā vidējā lielumu
starpība;
·
faktiskā un teorētiskā rezultatīvās
pazīmes lielumu starpība.
Ir svarīgi izprast šo sakarību ekonometrisko
saturu. No vienādības (b) seko, ka
yi-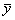 = (
= ( i -
i -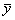 ) + (yi -
) + (yi - i). (c)
i). (c)
Kāpinot visus locekļus kvadrātā, vienādība nav
spēkā
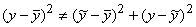 . (d)
. (d)
Bet, kā pierāda matemātiskā statistika,
vienādība atjaunojas, ja šādus noviržu kvadrātus summē pa visu statistisko kopu
(kurai aprēķināts vidējais 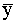 un regresijas
vienādojums
un regresijas
vienādojums 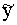 i aprēķināšanai).
i aprēķināšanai).
S (yi-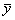 )2=S(
)2=S( i -
i -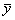 )2 + S(yi
-
)2 + S(yi
- i)2 . (9.20)
i)2 . (9.20)
Dispersijas analīzē parasti kopējo noviržu
kvadrātu summu apzīmē ar Q, izskaidroto noviržu kvadrātu summu ar Qf
(faktorālā), bet neizskaidroto - ar Qz. Tad iepriekšējo sakarību var
pierakstīt īsāk
Q=Qf
+Qz. (9.21)
Izteiksmē (9.20) summēšana jāizdara pa visu
statistisko kopu. Sakarība nav spēkā pa atsevišķām vienībām kā arī pa kopas
daļām.
Sakarība (9.20) rāda, ka rezultatīvās pazīmes
individuālo datu noviržu no aritmētiskā vidējā kvadrātu summa sastādās no divām
daļām:
·
teorētisko lielumu noviržu no vidējā
aritmētiskā kvadrātu summas;
·
faktisko lielumu (datu) noviržu no
teorētiskajiem lielumiem kvadrātu summas.
Pirmais saskaitāmais raksturo teorētisko lielumu
variāciju ap vidējo, tātad to rezultatīvās pazīmes variācijas daļu, kas
saistīta ar faktorālās pazīmes izmaiņām. Otrs saskaitāmais - faktisko datu
variāciju ap teorētiskajiem, tātad to variācijas daļu, kas nav saistīta ar
faktorālās pazīmes izmaiņām. Variāciju šajā gadījumā mērī ar noviržu kvadrātu
summām. Pirmo daļu sauc par izskaidroto, bet otru par neizskaidroto jeb
atlikuma noviržu kvadrātu summu.
Līdzīga sakarība ir starp dispersijām. Dalot
sakarības (9.20) visus locekļus ar kopas vienību skaitu n, iegūst dispersijas:
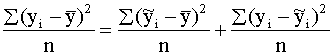 ,
,
kur 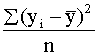 =s2y - visa jeb parastā rezultatīvās
pazīmes dispersija;
=s2y - visa jeb parastā rezultatīvās
pazīmes dispersija;
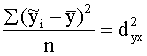 - izskaidrotā
dispersija;
- izskaidrotā
dispersija;
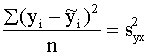 - neizskaidrotā jeb
atlikuma dispersija.
- neizskaidrotā jeb
atlikuma dispersija.
Līdz ar to visa dispersija ir sadalīta
izskaidrotajā un neizskaidrotajā daļā
s2y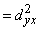 +
+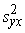 , (9.22)
, (9.22)
kas atbilst dispersiju saskaitīšanas teorēmai.
Piezīme. Šī sakarība ir pilnīgi precīza, ja
apstrādā ģenerālkopas datus, tāpat, ja, apstrādājot izlases datus, neņem vērā
brīvības pakāpju skaita zudumus. Ja tos ņem vērā, tad kopējo dispersiju
aprēķina ar n-1 brīvības pakāpēm, bet izskaidroto un neizskaidroto dispersiju
(ja regresijas vienādojumā ir divi parametri) - ar n-2 brīvības pakāpēm. Dalot
sakarības (9.20) kreiso pusi ar n-1, bet labo ar n-2, sakarība kļūst aptuvena
un precīzāka tad, ja n ir samērā liels skaitlis.
Salīdzinot izskaidroto un neizskaidroto
dispersiju, var spriest par sakarību ciešumu. Jo lielāka ir izskaidrotā un
mazāka ir neizskaidrotā dispersija, jo sakarība ir ciešāka un otrādi.
Parasti aprēķina kopējo un neizskaidroto
dispersiju. Izskaidroto dispersiju atrod, atņemot neizskaidroto dispersiju no
kopējās dispersijas. Jo s2y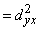 +
+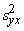 .
.
Neizskaidroto jeb atlikuma dispersiju,
izmantojot izlases datus, var aprēķināt ar iepriekšminēto formulu (definīcijas
formula):
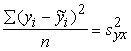 , (9.23)
, (9.23)
bet tās nenobīdītu vērtējumu ar formulu  . (9.24)
. (9.24)
Minētās formulas uzskatāmas par pamatformulām,
jo viņu saturs atbilst definīcijai. No skaitļošanas darba samazināšanas
viedokļa izdevīgāk lietot pārveidotas formulas, kuras neprasa aprēķināt
faktisko datu novirzes no teorētiskajiem lielumiem visām kopas vienībām.
Izdevīgi lietot šādu formulu:
Qz=Sy2-aSy-bSxy (9.25)
un
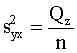 . (9.26)
. (9.26)
Formulas (9.25) lietošanai nepieciešamās summas Sy un Syx ir
aprēķinātas agrāk, jo tās nepieciešamas, sastādot normālvienādojumu sistēmu.
Lielumi a un b ir regresijas parametri, kuri aprēķināti no iepriekš minētās
normālvienādojumu sistēmas. Summa Sy2
ir jāaprēķina korelācijas koeficienta un vērtējuma standartkļūdas noteikšanai.
To nav grūti izdarīt, izstrādājot kopējo darba tabulu.
Izmantojot 9.5. tabulas datus, var aprēķināt
visas dispersijas apskatītajam piemēram, t. i., regresijas vienādojumam 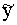 =6,64+0,2381x, kurš modelē pārtikas izdevumu atkarību no
mājsaimniecību ienākumiem.
=6,64+0,2381x, kurš modelē pārtikas izdevumu atkarību no
mājsaimniecību ienākumiem.
Kopējo jeb parasto noviržu kvadrātu summu un
dispersiju aprēķinām ar momentu formulām:
Q=Sy2-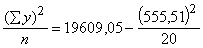 = 4179,482 (mērvienības nav);
= 4179,482 (mērvienības nav);
s2y=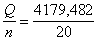 =208,974 (mērvienības nav);
=208,974 (mērvienības nav);
sy= 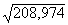 =14,46 (lati).
=14,46 (lati).
Neizskaidroto noviržu kvadrātu summu un
dispersiju aprēķinām ar formulām (9.25) un (9.26):
Qz=19609,05-6,6439×555,51-0,238096×64604,28=
=536,278 (mērvienības nav);
s2y×x=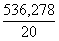 =26,814 (mērvienības nav);
=26,814 (mērvienības nav);
Izskaidroto dispersiju atrod kā kopējās un
neizskaidrotās dispersijas starpību d2y×x=s2y-s2y×x=208,974-26,814=182,160.
(skat. (9.22))
Kad tas ir izdarīts, aprēķinu pārbaudes nolūkos
var izskaitļot determinācijas koeficientu kā izskaidrotās un kopējās
dispersijas attiecību.
D=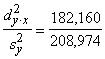 =0,87169.
=0,87169.
Tas sakrīt ar iepriekš aprēķināto korelācijas
koeficienta kvadrātu. Pēdējie zīmīgie cipari var atšķirties dažādu
starprezultātu noapaļojumu rezultātā.
9.4.3 Vērtējuma standartkļūda un
robežkļūda.
Ja mēģinātu interpretēt noviržu kvadrātu summas
un dispersijas, tām būtu jāuzrāda kā formāla mērvienība sākotnējās rezultatīvās
pazīmes vienības kvadrāts. Bet nav profesionālas jēgas latiem kvadrātā vai
kilogramiem kvadrātā. Šādai formālai mērvienībai ir sava nozīme tikai tad, ja
grib mainīt sākotnējo vienību, piemēram, pāriet no kilogramiem uz centneriem.
Tad vidējie un citi ar šo vienību saistītie lielumi ir jādala ar 100, bet
dispersijas un noviržu kvadrātu summas ar 1002=10000.
Lai iegūtu ar reālu vienību saistītus rādītājus,
no visām dispersijām aprēķina kvadrātsaknes.
Kvadrātsakne no
parastās dispersijas ir statistikā labi pazīstamā standartnovirze jeb
vidējā kvadrātiskā novirze:
sy=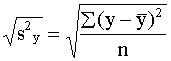 .
.
Analogi kvadrātsakne no neizskaidrotās
dispersijas ir vērtējuma pēc regresijas vienādojuma standartkļūda, kuru
vienkāršāk sauc par vērtējuma standartkļūdu. To sauc arī par atlikuma standartkļūdu
sy×x=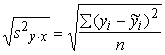 (9.27)
(9.27)
un
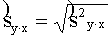 . (9.28)
. (9.28)
Piemērā pārtikas izdevumu vidējā kvadrātiskā
novirze ir sy=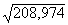 =14,46 (lati), bet vērtējuma standartkļūda sy×x=
=14,46 (lati), bet vērtējuma standartkļūda sy×x=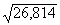 =5,18(lati). Pēdējās īpatsvaru (daļu) no pirmās nerēķina.
Tādu īpatsvaru rēķina, izmantojot atbilstošās dispersijas.
=5,18(lati). Pēdējās īpatsvaru (daļu) no pirmās nerēķina.
Tādu īpatsvaru rēķina, izmantojot atbilstošās dispersijas.
Vērtējuma
standartkļūdas īpašības un
lietošana.
Vērtējuma standartkļūda ir neizskaidrotās
variācijas absolūtā lieluma mērs. Tā ir nosaukts skaitlis un izteikta rezultatīvās
pazīmes mērvienībās. Vienā piemērā - latos, otrā - kilogramos.
Ja sakarības starp pētāmām pazīmēm nav, tad
regresijas vienādojums var nesaturēt faktoru - argumentu x un regresijas
vienādojumu var pierakstīt formā 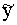 =a, kur a=
=a, kur a=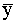 . Tādā gadījumā izskaidrotā dispersija ir nulle un
neizskaidrotā vienāda ar kopējo dispersiju. No tā seko, ka sy×x£ sy.
. Tādā gadījumā izskaidrotā dispersija ir nulle un
neizskaidrotā vienāda ar kopējo dispersiju. No tā seko, ka sy×x£ sy.
Ja sakarības starp pētāmām pazīmēm ir
funkcionālas, tad visas starpības yi-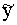 i ir nulles. Korelācijas diagrammā visi punkti
atrodas uz regresijas līnijas. Visu rezultatīvās pazīmes y variāciju izskaidro
faktorālās pazīmes x variācija. No tā seko, ka sy×x³0.
i ir nulles. Korelācijas diagrammā visi punkti
atrodas uz regresijas līnijas. Visu rezultatīvās pazīmes y variāciju izskaidro
faktorālās pazīmes x variācija. No tā seko, ka sy×x³0.
Līdz ar to vērtējuma standartkļūda vienmēr
atrodas apgabalā, ko ierobežo dubultnevienādība:
0£ sy×x£sy.
(9.29)
Ja sākotnējie dati veido normālu vai tam tuvu
sadalījumu, tad arī starpības yi- i veido normālu vai tam tuvu sadalījumu. Tādā
gadījumā vērtējuma standartkļūdu var interpretēt, izmantojot normālā sadalījuma
īpašības. Pareizinot standartkļūdu ar varbūtības koeficientu tp,
iegūst robežkļūdu Dy×x:
i veido normālu vai tam tuvu sadalījumu. Tādā
gadījumā vērtējuma standartkļūdu var interpretēt, izmantojot normālā sadalījuma
īpašības. Pareizinot standartkļūdu ar varbūtības koeficientu tp,
iegūst robežkļūdu Dy×x:
Dy×x=tp×sy×x.
(9.30)
Varbūtības koeficients tp brīvi
izvēlētām varbūtībām P ņem no normālā sadalījuma tabulām, ja izlase ir liela,
vai no Stjūdenta t tabulām, ja izlase maza.
Atskaitot un pieskaitot robežkļūdu rezultatīvās
pazīmes teorētiskajiem lielumiem, dabūjam vērtējuma apgabala robežas. Starp
šīm robežām ir ietverts vērtējuma apgabals. Vērtējuma apgabalu var pierakstīt
šādi:
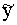 i -Dy×x£ yi£
i -Dy×x£ yi£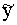 i+Dy×x
(9.31)
i+Dy×x
(9.31)
Vērtējuma apgabala jēdziens kļūst skaidrāks,
aplūkojot tā ģeometrisko attēlu.
Vērtējuma robežas var attēlot korelācijas
diagrammā ar taisnēm. Šīs taisnes ir paralēlas regresijas taisnei un atrodas no
tās, mērot pa vertikāli, robežkļūdas attālumā (skat. 9.11. attēlu).
Ja vērtējuma apgabalu nosaka ar varbūtību 0,683,
tad lielas izlases gadījumā varbūtības koeficients ir viens un robežkļūda
vienāda ar standartkļūdu Dy×x=sy×x.
Ja korelācijas diagrammā novelk regresijas taisnei divas paralēlas taisnes,
kuras atrodas, mērot pa vertikāli, vienas standartkļūdas attālumā, tad starp
tām teorētiski jāatrodas ap 68% punktu korelācijas diagrammā, pie tam pa katru
pusi no regresijas taisnes aptuveni 34%
(skat. 9.11. attēlu).
Ja regresijas līnijai novelk divas paralēlas
taisnes divu standartkļūdu attālumā (Dy×x=2sy×x),
tad starp tām jāatrodas aptuveni 95,4% novērojumu. Starp divām paralēlām
taisnēm trīs standartkļūdu attālumā (Dy×x=3sy×x)
jāatrodas praktiski visām atzīmēm korelācijas diagrammā.
Šīs īpašības var izmantot grafiskās un
matemātiskās analīzes rezultātu savstarpējai salīdzināšanai un pārbaudei.
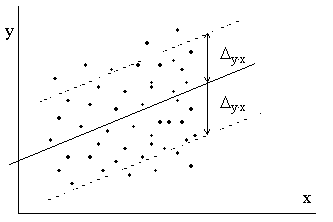
9.11. attēls. Vērtējuma pēc regresijas
vienādojuma robežkļūdu grafisks attēls.
Neizskaidrotās dispersijas un vērtējuma
standartkļūdas nenobīdītos vērtējumus lieto tad, ja secinājumus grib attiecināt
nevien uz apstrādāto datu kopu, bet uz ģenerālkopu no kuras apstrādātie dati
ņemti kā gadījumizlase. Tad jārēķinās, ka vērtējuma kļūda var būt lielāka nekā
iepriekš aprēķināts, īpaši ja izlase ir maza. Lai to fiksētu, izdara vajadzīgo
rādītāju korekciju ar t. s. brīvības pakāpju skaita zudumu.
Neizskaidrotā dispersija pēc šādas korekcijas
būs 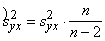 =26,814
=26,814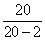 =29,793, bet vērtējuma standartkļūda
=29,793, bet vērtējuma standartkļūda 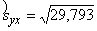 =5,46 (lati).
=5,46 (lati).
Vērtējuma standartkļūdas ekonometrisku lietojumu
parādīsim, izmantojot lauksaimniecības piemēru, jo saimnieciskās darbības
analīzē šis lietojums ir uzskatāmāks.
Iepriekš aprēķinājām, ka kādas saimniecības
teorētiski sagaidāmais izslaukums vidēji no govs ir 3783 kg, bet faktiski
iegūtais izslaukums ir 3600 kg gadā, tātad ražošanas potenciāls nav izmantots
par 183 kg. Palika neatbildēts jautājums, vai šī negatīvā novirze ir uzskatāma
par tik lielu, lai saimniecisko darbību vērtētu krasi negatīvi, vai tā ir tik
maza, ka viņu var uzlūkot vienkārši kā nejaušu faktoru darbības rezultātu.
Vienkāršākajā gadījumā šo novirzi salīdzina ar
vērtējuma standartkļūdu. Ja faktiskā novirze pārsniedz standartkļūdu, tā
jāvērtē kā būtiska, ja nē - to var uzskatīt kā nejaušību.
Vērtējuma standartkļūda aprēķinos izmantotai
izslaukuma funkcijai ir sy×x=189kg,
bet tās nenobīdītais vērtējums 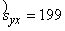 kg. Faktiskā novirze ir nedaudz mazāka par šo lielumu. Tātad
konkrētās saimniecības darbs ir jāvērtē kā tuvs kritiski negatīvam, tomēr šajā
kritiskajā apgabalā nenonāk.
kg. Faktiskā novirze ir nedaudz mazāka par šo lielumu. Tātad
konkrētās saimniecības darbs ir jāvērtē kā tuvs kritiski negatīvam, tomēr šajā
kritiskajā apgabalā nenonāk.
Ja grib precīzāku atbildi, var aprēķināt kāda ir
varbūtība, ka saimnieciskais darbs būs tik slikts vai sliktāks, kā atzīmēts
vērtējamā saimniecībā.
Šim nolūkam jāaprēķina varbūtības koeficients t=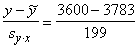 =-0,92 un jāatrod normālā sadalījuma tabulās varbūtība, ka
punkts atradīsies ārpus šī koeficienta izdalītā apgabala (vienpusējs kritērijs)
P=0,5-y(0,92)=0,5-0,321=0,18.
=-0,92 un jāatrod normālā sadalījuma tabulās varbūtība, ka
punkts atradīsies ārpus šī koeficienta izdalītā apgabala (vienpusējs kritērijs)
P=0,5-y(0,92)=0,5-0,321=0,18.
Tik sliktu spēkbarības izmantošanu, kāda bijusi
šajā saimniecībā, vai vēl sliktāku var sagaidīt ar varbūtību 0,18.
Citiem vārdiem tik slikta un vēl sliktāka
spēkbarības izmantošana ir raksturīga 18% saimniecību.
Šādi un līdzīgi ražošanas potenciāla un tā
izmantošanas vērtējumi tirgus ekonomikas apstākļos ir vajadzīgi:
·
uzņēmuma vadītājam sava darba
pašvērtēšanai;
·
kredītu pieprasījumu pamatošanai un šo
pieprasījumu ekspertīzei;
·
saimniecības ienesības un vērtības
noteikšanai pirkšanas - pārdošanas gadījumā u. c.
9.5. Vienkāršās regresijas un korelācijas
rādītāju izlases kļūdas
un nulles hipotēžu pārbaude
9.5.1. Regresijas koeficienta
standartkļūda un robežkļūda
Regresijas vienādojumu un korelācijas
koeficientu bieži aprēķina pēc izlases datiem. Ir lietderīgi uzskatīt, ka
regresijas un korelācijas rādītāji aprēķināti pēc izlases datiem arī tad, ja
īstenībā izmantoti ģenerālkopas dati, jo parasti mūs neinteresē vienkārša faktu
konstatācija ierobežotā ģenerālkopā, bet vispārēja likumsakarība, kas saista
pētāmos objektus un parādības. Šādā gadījumā statistiskie secinājumi
jāattiecina uz iedomātu hipotētisku ģenerālkopu, kura vienmēr ir plašāka, nekā
aptver savāktie dati.
Līdzīgi, kā dara, vērtējot aritmētisko vidējo,
var iedomāties, ka no vienas un tās pašas ģenerālkopas ņemtas daudzas viena
lieluma izlases un katrai aprēķināts savs regresijas vienādojums. Šie
regresijas vienādojumi, protams, būs atšķirīgi. Atšķirības rada nenovēršama
izlases kļūda.
Pēc daudzu no vienas kopas ņemtu vienāda lieluma
izlašu datiem aprēķinātie regresijas koeficienti, tāpat kā aritmētiskie
vidējie, veido sadalījumu, kurš tuvs normālajam, ja vien pētāmā kopa pēc abām
saistītajām pazīmēm aptuveni atbilst normālā sadalījuma likumam un izlašu
lielums ir pietiekami liels. Tādēļ regresijas koeficienta izlases kļūdas
vērtēšanā var izmantot parasto shēmu un Stjudenta sadalījuma tabulas.
Ievērojot šos nosacījumus, regresijas
koeficienta standartkļūda 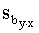 ir tieši proporcionāla regresijas vienādojuma vērtējuma
standartkļūdai
ir tieši proporcionāla regresijas vienādojuma vērtējuma
standartkļūdai 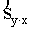 un apgriezti
proporcionāla faktorālās pazīmes standartkļūdei sx un kvadrātsaknei
no izlases kopas vienību skaita
un apgriezti
proporcionāla faktorālās pazīmes standartkļūdei sx un kvadrātsaknei
no izlases kopas vienību skaita 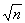 :
:
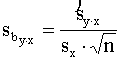 . (9.32)
. (9.32)
Regresijas koeficienta robežkļūdu 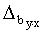 aprēķina, pareizinot
standartkļūdu ar varbūtības koeficientu tp:
aprēķina, pareizinot
standartkļūdu ar varbūtības koeficientu tp:
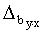 = tp×
= tp×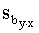 . (9.33)
. (9.33)
Ja tas nerada pārpratumus, apzīmējumus var
vienkāršot, apzīmējot regresijas koeficienta standartkļūdu ar sb,
robežkļūdu ar Db.
Regresijas koeficienta vērtējuma robežas ar
izvēlētajām varbūtībām P1 un P2 ir
b
-Db£ b £b+Db,
(9.34)
kur b
- ģenerālās kopas regresijas koeficients, kura nezināmo lielumu vērtējam.
Ja P1 = P2, tad var
izmantot abpusējās integrālās tabulas, ja P1 ¹ P2,
jāizmanto vienpusējās tabulas, un varbūtību koeficienti apakšējai un augšējai
robežai jānosaka patstāvīgi.
Regresijas koeficienta robežkļūdas un līdz ar to
arī standartkļūdas kā robežkļūdas speciālgadījums, kad tp = 1,
ģeometriska interpretācija ir šāda (9.12. attēls). Ar izvēlēto varbūtību var
apgalvot, ka nezināmā ģenerālkopas regresijas taisne atrodas leņķu pārī, kuru
virsotnes ir punktā ar koordinātēm 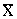 ,
, 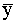 un tos veido divas
taisnes PP' un QQ' ar leņķu koeficientiem b-Db
un b+Db.
Konstruējot taisnes PP' un QQ', jāizmanto vienādojumi, kuri uzrakstīti mainīgo
lielumu novirzēs no vidējiem:
un tos veido divas
taisnes PP' un QQ' ar leņķu koeficientiem b-Db
un b+Db.
Konstruējot taisnes PP' un QQ', jāizmanto vienādojumi, kuri uzrakstīti mainīgo
lielumu novirzēs no vidējiem:
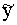 -
- 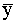 = (b - Db)
(x -
= (b - Db)
(x - 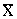 ),
),
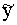 -
- 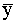 = (b + Db)
(x -
= (b + Db)
(x - 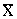 ). (9.35)
). (9.35)
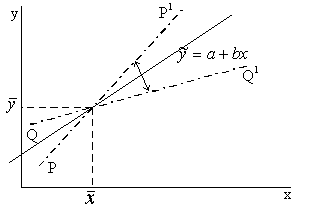
9.12. attēls. Regresijas
koeficienta izlases kļūdas grafisks attēls
Vienādojumi sākotnējās mērvienībās  =a + (b ±
Db)x
pareizus rezultātus nedod.
=a + (b ±
Db)x
pareizus rezultātus nedod.
Aprēķināsim dzīves līmeņa piemēra regresijas
koeficienta b=0,2381 standartkļūdu. Jau bija aprēķināts 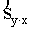 = 5,4583. Vienību
skaits izlasē n = 20. Vēl jāaprēķina faktorālās pazīmes standartnovirze, ko
ērti izdarīt ar momentu formulu (dati no 9.5. tabulas kopsummas rindas)
= 5,4583. Vienību
skaits izlasē n = 20. Vēl jāaprēķina faktorālās pazīmes standartnovirze, ko
ērti izdarīt ar momentu formulu (dati no 9.5. tabulas kopsummas rindas)
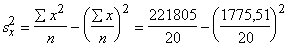 = 3209,16;
= 3209,16;
sx=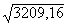 =56,649.
=56,649.
Tagad ir visi skaitļi, ko ietvert regresijas
koeficienta standartkļūdas formulā
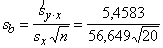 =0,0215.
=0,0215.
Lai aprēķinātu robežkļūdu, izvēlas varbūtību, ar
kuru grib garantēt vērtējuma apgabala pareizību. Tā, piemēram, izvēlamies P=0,9
un nosakām simetrisku pieļaujamo apgabalu, jo vienlīdz nozīmīgas ir abos
virzienos pieļautās kļūdas. Tad no Stjūdenta sadalījuma kritisko vērtību
tabulām var nolasīt, ka varbūtībai 0,9 un 18 brīvības pakāpēm atbilst
varbūtības koeficients tp=1,73. Līdz ar to saskaņā ar formulu (9.33)
Db=1,73×0,0215=0,0372.
Vērtējamais regresijas koeficients b ar varbūtību
0,9 sagaidāms robežās, ko nosaka dubultnevienādība (9.34)
0,2381-0,0372 £
b £ 0,2381+0,0372;
0,2009£
b £ 0,2753.
Ar varbūtību 0,9 var sagaidīt, ka atbilstošais
regresijas koeficients ģenerālkopā, no kuras ņemta izlase, nav mazāks par
0,2009 un nav lielāks par 0,2753.
Piemēra ietvaros ar varbūtību 0,9 var sagaidīt,
ka pieaugot iedzīvotāju ienākumiem, rēķinot uz vienu mājsaimniecības locekli
par 1 latu, papildus izdevumi pārtikas produktu iegādei nebūs mazāki par 20
santīmiem un nebūs lielāki par 28 santīmiem.
Izlases kļūdas iznāca samērā lielas tādēļ, ka
izlase mācību nolūkos ņemta ļoti maza. Reālos ekonometrijas pētījumos parasti
jāņem dažus simtus vai tūkstošu vienību lielas izlases.
9.5.2. Regresijas vienādojuma brīvā
locekļa standartkļūda un robežkļūda
Pēc izlases datiem noteikta regresijas taisne
arī pēc novietojuma (pacēluma) virs abscisu ass atšķirsies no analogas taisnes,
kas aprēķināta pēc ģenerālkopas datiem. Tas nozīmē, ka arī regresijas
vienādojuma brīvais loceklis satur izlases kļūdu.
Regresijas vienādojuma brīvā locekļa standartkļūdu
aprēķina ar formulu
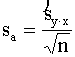 . (9.36)
. (9.36)
Iepriekšējā piemēra regresijas vienādojuma brīvā
locekļa 6,64 standartkļūda ir
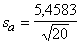 = 1,22.
= 1,22.
Regresijas vienādojuma (9.13. attēls) brīvā
locekļa standartkļūdu ģeometriski var interpretēt šādi. Ar varbūtību 0,68 (tp
= 1) var sagaidīt, ka vienādojuma brīvā locekļa kļūdas dēļ ģenerālkopas
regresijas taisne atrodas starp divām izlases regresijas taisnei paralēli
novilktām taisnēm, kuras atrodas no izlases regresijas taisnes sa
attālumā, mērot pa vertikāli.
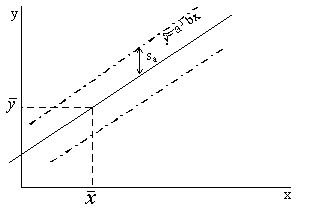
9.13.
attēls. Regresijas vienādojuma brīvā locekļa izlases kļūdas grafisks attēls
Šī standartkļūda ir jāatšķir no vērtējuma pēc
regresijas vienādojuma standartkļūdas sy×x.
Vienādojuma brīvā locekļa standartkļūda atspoguļo izlases kļūdu, un tā
samazinās, palielinot izlases vienību skaitu, bet vērtējuma standartkļūda sy×x
atspoguļo neizskaidroto variāciju un no izlases lieluma praktiski nav atkarīga.
Regresijas vienādojuma brīvā locekļa robežkļūdu
atrod kā parasti, pareizinot standartkļūdu ar varbūtības koeficientu.
Ja ņem to pašu varbūtību, ko izmantojām regresijas koeficienta vērtēšanā, 0,9
tad
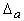 =tp × sa
= 1,73 ×
1,22 = 2,11.
=tp × sa
= 1,73 ×
1,22 = 2,11.
Nezināmā ģenerālkopas vienādojuma brīvā locekļa a vērtējuma
robežas un apgabals ir šādi:
a - 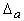 £ a £ a +
£ a £ a + 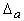 ;
;
Piemērā
6,64 - 2,11 £
a £ 6,64 + 2,11;
4,53 £
a £ 8,75.
5.3 Regresijas vienādojuma un vērtējuma
pilnā kļūda
Zinot regresijas vienādojuma koeficienta un
brīvā locekļa izlases kļūdu aprēķināšanas metodes, var izvirzīt jautājumu par
visa regresijas vienādojuma kopējās izlases kļūdas aprēķināšanu. Tas nozīmē, ka
jānosaka standartkļūdas un robežkļūdas teorētiskiem lielumiem, kas
saistīti ar noteiktām faktorālās pazīmes vērtībām.
Regresijas vienādojumu, kurš ir teorētisko
lielumu aprēķināšanas formula, var pierakstīt šādā veidā:
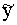 =
= 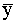 +b(x -
+b(x -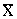 ) (skat.
(9.12)).
) (skat.
(9.12)).
No tā redzams, ka teorētisko lielumu 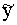 izlases kļūda ietver
vidējā lieluma
izlases kļūda ietver
vidējā lieluma 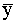 un regresijas
koeficienta izlases kļūdas. Vidējā lieluma kļūdu šajā gadījumā var samazināt
līdz regresijas vienādojuma brīvā locekļa kļūdai.
un regresijas
koeficienta izlases kļūdas. Vidējā lieluma kļūdu šajā gadījumā var samazināt
līdz regresijas vienādojuma brīvā locekļa kļūdai.
No dispersiju saskaitīšanas teorēmas ir zināms,
ka apvienoto kļūdu šādos gadījumos var iegūt, summējot atsevišķo kļūdu
kvadrātus. Bez tam ir zināms, ka konstanta lieluma un mainīga lieluma
reizinājuma dispersija ir vienāda ar mainīgā lieluma dispersiju, pareizinātu ar
konstantā lieluma kvadrātu. Tātad regresijas standartkļūdas kvadrāts  ir šāds:
ir šāds:
 =
=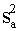 +
+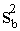 (x -
(x - 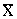 )2 . (9.37)
)2 . (9.37)
Ievietojot izteiksmē (9.37) abu jau iepriekš
aprēķināto kļūdu vērtības no formulām (9.32) un (9.36), iegūstam:
 =
=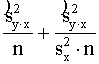 (x -
(x - 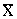 )2 . (9.38)
)2 . (9.38)
Ņemot vērtējuma standartkļūdu  ārpus iekavām un
aprēķinot no abām pusēm kvadrātsakni, iegūstam regresijas vienādojuma
standartkļūdas (izlases kļūdas) formulu:
ārpus iekavām un
aprēķinot no abām pusēm kvadrātsakni, iegūstam regresijas vienādojuma
standartkļūdas (izlases kļūdas) formulu:
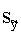 =
=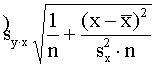 . (9.39)
. (9.39)
Šī standartkļūda ir jāatšķir no vērtējuma pēc
regresijas vienādojuma standartkļūdas sy×x.
Regresijas standartkļūda 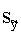 atspoguļo izlases
kļūdu, un to lieto tikai tad, ja apstrādājamos datus uzskata par izlasi;
vērtējuma standartkļūda sy×x
atspoguļo neizskaidroto variāciju, un tā jāņem vērā vienmēr, kad pētāmās
sakarības ir korelatīvas.
atspoguļo izlases
kļūdu, un to lieto tikai tad, ja apstrādājamos datus uzskata par izlasi;
vērtējuma standartkļūda sy×x
atspoguļo neizskaidroto variāciju, un tā jāņem vērā vienmēr, kad pētāmās
sakarības ir korelatīvas.
No formulas (9.39) redzams, ka pie fiksētiem
pārējiem lielumiem regresijas izlases kļūda samazinās, palielinot izlases
lielumu n. Robežgadījumā, ja n®¥,
šī kļūda tiecas uz nulli. Fiksējot nemainīgā līmenī visus pārējos lielumus,
izlases kļūda ir atkarīga no faktorālās pazīmes x vērtībām. Tā palielinās,
palielinoties novirzes (x - 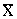 ) absolūtajai vērtībai. Līdz ar to regresijas standartkļūdu
nevar izteikt ar vienu skaitli; katrai argumenta vērtībai tā ir citāda.
) absolūtajai vērtībai. Līdz ar to regresijas standartkļūdu
nevar izteikt ar vienu skaitli; katrai argumenta vērtībai tā ir citāda.
Regresijas standartkļūdu var attēlot ģeometriski
ar divām liektām līnijām (9.14. attēls). Līniju attālumu no regresijas taisnes,
mērot pa vertikāli, nosaka formula (9.39).
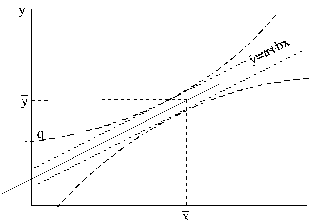
9.14.
attels. Regresijas vienādojuma izlases kļūdas grafisks attēls.
Regresijas robežkļūdu aprēķina parastā kārtībā,
pareizinot standartkļūdu ar varbūtības koeficientu.
Vērtējuma pilnās kļūdas kvadrātu,
atbilstoši dispersiju saskaitīšanas teorēmai, aprēķina, summējot vērtējuma
standartkļūdas sy×x
kvadrātu un regresijas vienādojuma standartkļūdas 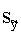 kvadrātu:
kvadrātu:
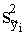 =
=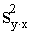 +
+ . (9.40)
. (9.40)
Ievietojot šajā izteiksmē  vietā tā nozīmi no
iepriekšējās formulas, ņemot
vietā tā nozīmi no
iepriekšējās formulas, ņemot 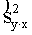 ārpus iekavām un no
abām pusēm aprēķinot kvadrtātsakni, iegūstam vērtējuma pilnās kļūdas formulu:
ārpus iekavām un no
abām pusēm aprēķinot kvadrtātsakni, iegūstam vērtējuma pilnās kļūdas formulu:
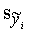 =
=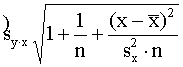 . (9.41)
. (9.41)
Formula (9.41) no (9.39) atšķiras ar pozitīvu
vieninieku zemsaknes izteiksmē. To loģiskā atšķirība ir šāda. Neierobežoti
palielinot izlases lielumu n, var panākt pēc patikas mazu izlases kļūdu. Šādā
gadījumā regresijas standartkļūda (9.39) tiecas uz nulli. Bet ar šādu paņēmienu
nevar samazināt neizskaidroto variāciju. Tādēļ vērtējuma pilnā kļūda,
neierobežoti palielinot izlases lielumu, tiecas uz vērtējuma standartkļūdu sy×x.
Šajā gadījumā zūd tā kļūdas daļa, ko radījusi izlases metodes lietošana, bet
paliek tā daļa, ko neizskaidro regresijas vienādojums, resp., faktorālās
pazīmes variācija.
Vērtējuma pilno robežkļūdu atrod, vērtējuma
pilno standartkļūdu (9.41) pareizinot ar varbūtības koeficientu.
Vērtējuma pilnās standartkļūdas un robežkļūdas
norobežoto apgabalu var attēlot grafiski ar divām liektām līnijām (9.15.
attēls), kuras atrodas abās pusēs regresijas taisnei, bet tālāk no tās,
salīdzinot ar atbilstošajām regresijas izlases kļūdu līnijām.
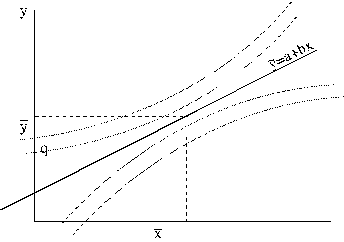
9.15.
attēls. Vērtējuma pēc regresijas vienādojuma pilnās kļūdas grafisks attēls.
Regresijas vienādojuma izlases kļūdu un
regresijas vienādojuma pilno kļūdu lieto tad, ja ir nepieciešams precīzāk
izvērtēt ar regresijas vienādojumu aprēķinātos rezultatīvās pazīmes teorētiskos
lielumus.
Ja vien izlase nav ļoti maza, tad ar regresijas
vienādojumu neizskaidrotā variācija parasti ir daudz lielāka nekā pašas
regresijas izlases kļūda. Tādēļ parasti, ja precizitāte nav vajadzīga sevišķi
liela, aprobežojas ar vērtējuma pēc regresijas vienādojuma standartkļūdu un
robežkļūdu, kuras aprēķināt daudz vienkāršāk.
Regresijas vienādojuma izlases kļūda un
regresijas pilnā kļūda ir vairāk vajadzīgas, ja regresijas vienādojumu kā
modeli izmanto ārpus faktisko datu variācijas apgabala t. s. ekstrapolācijas
apgabalā. Tad, pieaugot novirzēm x - 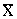 , regresijas vienādojuma izlases un pilnā kļūda jau
ievērojami atšķiras no parastās vērtējuma standartkļūdas. Precīzākās formulas
tad uzskatāmi parāda, ka šāda ekstrapolācija ir daudz nedrošāka nekā vērtējumi
faktisko datu variācijas apgabalā.
, regresijas vienādojuma izlases un pilnā kļūda jau
ievērojami atšķiras no parastās vērtējuma standartkļūdas. Precīzākās formulas
tad uzskatāmi parāda, ka šāda ekstrapolācija ir daudz nedrošāka nekā vērtējumi
faktisko datu variācijas apgabalā.
9.5.4 Korelācijas koeficienta izlases
vērtējuma apgabals
Standartkļūda ir objektīvs izlases kļūdas
lieluma mērs tad, ja rādītājs, kam to aprēķina, izlases atkārtojot, veido
normālu sadalījumu. Tāda īpašība ir aritmētiskam vidējam, regresijas
koeficientam un daudziem citiem rādītājiem. Pirmais priekšnoteikums, lai
sadalījums varētu būt normāls, ir vērtējamā rādītāja neierobežots variācijas
apgabals.
Ja no vienas un tās pašas ģenerālkopas ņem
daudzas vienāda lieluma izlases un katrai no tām aprēķina korelācijas
koeficientu, tad šie koeficienti veido sadalījumu, kurš ir atšķirīgs no normālā
sadalījuma. Korelācijas koeficienti nevar veidot normālu sadalījumu tādēļ, ka
to iespējamās vērtības ir samērā šaurā apgabalā -1 £ r £ +1. Izlases
korelācijas koeficientu sadalījums sevišķi stipri novirzās no normālā
sadalījuma tad, ja korelācijas koeficients ģenerālkopā ir augsts. Pieņemsim, ka
tas ir 0,9. Tālāk var pieņemt, ka pusē no izlasēm iegūstam lielāku un pusē
mazāku izlases korelācijas koeficientu nekā tas ir ģenerālajā kopā, 50%
gadījumos izlases korelācijas koeficientam jābūt robežās 0,9 < r < 1,0,
un 50% gadījumos tas var izkliedēties robežās -1 < r < 0,9. Tāds
sadalījums ir krasi asimetrisks, un tā pētīšanai normālā sadalījuma īpašības
izmantot nevar. (9.16. attēls)
Lai aprēķinātu korelācijas koeficienta vērtējuma
robežas, var izmantot pārveidojumu, kuru ieteicis Ronalds Fišers. Viņš
pierādījis, ka funkcijai z, kuras arguments ir korelācijas koeficients,
sadalījums ir ļoti tuvs normālajam. Funkcija z dota ar formulu (9.42).
z
=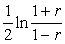 . (9.42)
. (9.42)
Aprēķinu vispārējā shēma ir šāda:
1. Aprēķina vai nolasa
speciālās tabulās funkcijas z vērtību, kura atbilst pēc izlases datiem
aprēķinātajam korelācijas koeficientam r (formula 9.42).
2. Aprēķina funkcijas z
standartkļūdu, izmantojot formulu:
sz
= 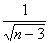 . (9.43)
. (9.43)
3. Zinot, ka funkcijai z
ir normāls sadalījums, nosaka tās vērtējuma robežas:
z
- tp sz £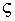 £
z + tp sz. (9.44)
£
z + tp sz. (9.44)
4. Aprēķina vai nolasa
speciālās tabulās z augšējai un apkšējai robežai atbilstošos korelācijas
koeficientus, kuri arī ir meklētās vērtējuma robežas. Aprēķinam izmanto inverso
formulu
r
= 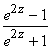 (9.45)
(9.45)
Pārtikas izdevumu piemērā korelācijas
koeficients r bija 0,9336.
1.Aprēķinām atbilstošo z
funkciju z =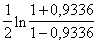 = 1,6857.
= 1,6857.
2.Aprēķinām z izlases
standartkļūdu sz = 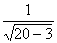 = 0,2425.
= 0,2425.
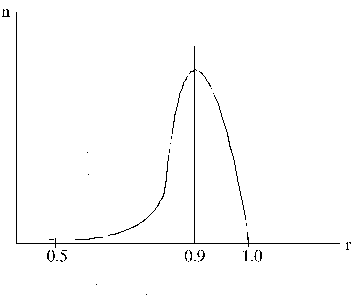
9.16. attēls.
Hipotētisks izlases korelācijas koeficienta
r sadalījums, ja ģenerālkopas
korelācijas koeficients r
= 0.9
3. Saglabājot iepriekš
izmantoto varbūtību 0,9 un tai atbilstošo varbūtības koeficientu 1,73,
aprēķinām funkcijas z vērtējuma apgabalu.
1,6857-
1,73 × 0,2425 < < 1,6857 + 1,73 ×
0,2425;
< 1,6857 + 1,73 ×
0,2425;
1,2662< < 2,1052.
< 2,1052.
4. Izdarām inverso
transformāciju no z robežām uz r robežām :
rmin
= 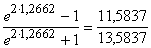 =0,8528;
=0,8528;
rmax
= 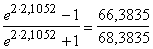 =0,9708.
=0,9708.
5. Pierakstām
korelācijas koeficienta vērtējuma apgabalu ģenerālajā kopā. Vērtējamo ģenerālkopas
korelācijas koeficientu apzīmē ar grieķu burtu r
(ro) : 0,8528£r£0,9708.
Izdarot aprēķinu loģisko pārbaudi,
jāpārliecinās, vai izlases korelācijas koeficients 0,9336 atrodas atrastajā
vērtējumu apgabalā.
Tātad ar varbūtību 0,9 var apgalvot, ka
iedzīvotāju naudas ienākumus un izdevumus pārtikas iegādei tajā ģenerālajā
kopā, no kuras ņemta izlase, saista korelācija ar sakarību ciešumu ne mazāku kā
r = 0,85 un ne lielāku ka r = 0.97.
9.5.5. Nulles hipotēžu pārbaude
Dažreiz nav nepieciešams aprēķināt regresijas un
korelācijas koeficientu vērtējumu robežas, bet pietiek pārbaudīt, vai pētītās
sakarības ir statistiski nozīmīgas. Šajā nolūkā izvirza hipotēzes,
saskaņā ar kurām attiecīgie koeficienti ģenerālajā kopā ir nulles, un pārbauda,
vai pēc izlases datiem aprēķinātie rādītāji atbilst šīm hipotēzēm.
Nulles hipotēzi, kas apgalvo, ka korelācijas
koeficients ģenerālkopā ir nulle, var pārbaudīt, izmantojot gatavas
skaitļošanas tabulas. Tabulās ir norādītas korelācijas koeficienta kritiskās
robežas, kuras empīriskajam korelācijas koeficientam pārsniedzot, nulles
hipotēzi noraida. Kritiskās robežas ir tabulētas n
= n - k brīvības pakāpēm, kur n - kopas vienību, bet k - vienādojuma parametru
skaits (pāru sakarību vienādojumā 2).
Mūsu piemērā n
= n - k = 20 - 2 = 18. Tam atbilst šādas kritiskās robežas: varbūtībai
0,95 (a
= 0,05) - 0,444; varbūtībai 0,99 (a
= 0,01) - 0,561. Pēc statistiskajiem datiem aprēķinātais r = 0,9336 ir daudz
lielāks. Tātad nulles hipotēzi var noraidīt ar vēl augstāku varbūtību. Līdz ar
to sakarības ir statistiski nozīmīgas.
Nulles hipotēzi var izvirzīt arī par regresijas
koeficientu. Tādā gadījumā empīriskā t attiecība ir šāda:
t
= 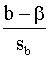 , (9.46)
, (9.46)
bet saskaņā ar hipotēzi b = 0, tādēļ
t
= 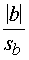 . (9.47)
. (9.47)
Atrasto t salīdzina ar Stjūdenta sadalījuma
kritiskajām robežām un pieņem lēmumu vispārējā kārtībā. Iepriekšējam piemēram b
= 0,2381; sb = 0,0215; t =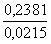 = 11,07.
= 11,07.
Ja vēlamies nulles hipotēzi pārbaudīt ar
varbūtību 0,99, tad atbilstoši 18 brīvības pakāpēm Stjudenta tabulās atrodam
kritisko robežu ta
= 2,87. Tā kā empīriskais t ir daudz lielāks par t kritisko robežu, nulles
hipotēzi var noraidīt ar varbūtību lielāku par 0,99. Izpētītās sakarības ir
statistiski nozīmīgas.
Jāatzīmē, ka ekonomikas pētījumos hipotēžu
pārbaudē tradicionāli izmantotie kritēriji
P = 0,95 un P = 0,99 ir stipri augsti. Tomēr literatūrā tos plaši lieto, gan
tradīcijas dēļ, gan tādēļ, ka šiem kritērijiem piemērotas tabulas visbiežāk
sastopamas skaitļošanas tabulu krājumos. Tomēr, ja konkrētais pētījums neprasa
tik augstu ticamību, tad vajadzētu izvēlēties zemāku varbūtību.
9.6. Daži papildjautājumi.
9.6.1. Saistītās regresijas
Pētot sakarības ekonomikā, parasti samērā viegli
noteikt, kura no pētāmām pazīmēm ir neatkarīga un kura atkarīga to savstarpējā
mijiedarbībā. Atkarīgos un neatkarīgos mainīgos lielumus nosaka, vadoties no to
kvalitatīvajām īpašībām, resp., no zināšanām, ko dod mikro vai makroekonomika,
kā arī inženierzinātnes vai lauksaimniecības zinātnes.
Taču nereti nākas sastapties ar statistiskām
pazīmēm, kuras atspoguļo tādus notikumus vai parādības, par kurām nevar
pateikt, kura no tām ir cēlonis un kura - sekas. Tad nevar izveidot
cēloņsakarību ķēdi "faktors - rezultāts". Šāds stāvoklis visbiežāk
izveidojas, apstrādājot izmēģinājumu un eksperimentu rezultātus.
Tā, piemēram, ir zināms, ka dažādu vielu saturu
augsnē (fosfora, kālija) var noteikt ar vairākām analīžu metodēm. Ja katrā
laukā analīze izdarīta ar divām metodēm, tad iegūtie dati ir cieši korelatīvi
saistīti. Taču nav iespējams pateikt, kuras analīzes rezultāts ir cēlonis un
kuras - sekas. Īstais cēlonis - patiesais fosfora saturs augsnē paliek
nezināms. To atspoguļo divi dažādi mērījumi, kuri no cēloņsakarību viedokļa ir
vienādi nozīmīgi. Līdzīgus piemērus var atrast citās zinātņu nozarēs.
Šādos gadījumos vienai un tai pašai sakarībai
var aprēķināt divus regresijas vienādojumus  =a+bx un
=a+bx un 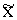 =a'+b'y. Ja ir zināms viens no šiem vienādojumiem, no tā
algebrisku pārveidojumu ceļā nevar atrast otru, jo katrs ir atrasts ar citiem
nosacījumiem. Pirmo atrod, minimizējot vertikālo noviržu kvadrātu summu Qy=S(y-
=a'+b'y. Ja ir zināms viens no šiem vienādojumiem, no tā
algebrisku pārveidojumu ceļā nevar atrast otru, jo katrs ir atrasts ar citiem
nosacījumiem. Pirmo atrod, minimizējot vertikālo noviržu kvadrātu summu Qy=S(y-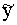 )2®min,
bet otro - minimizējot horizontālo noviržu kvadrātu summu Qx=S(x-
)2®min,
bet otro - minimizējot horizontālo noviržu kvadrātu summu Qx=S(x-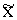 )2®min.
)2®min.
Regresijas vienādojumu 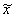 =a'+b'y un tai atbilstošo taisni grafiskajā attēlā sauc par
saistītu ar vienādojumu
=a'+b'y un tai atbilstošo taisni grafiskajā attēlā sauc par
saistītu ar vienādojumu  =a+bx un arī otrādi. Saistīto regresijas taišņu galvenās
īpašības ir šādas.
=a+bx un arī otrādi. Saistīto regresijas taišņu galvenās
īpašības ir šādas.
1.Ja sakarības starp
mainīgajiem lielumiem x un y nav, tad abas taisnes ir savstarpēji
perpendikulāras un krustojas punktā ar koordinātēm 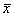 ;
;  . To vienādojumi ir
. To vienādojumi ir  =a un
=a un 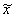 =a' jeb
=a' jeb  =
= un
un  =
=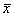 .
.
2.Ja sakarības ir
funkcionālas, tad abas regresijas līnijas sakrīt, resp., vienādojumu 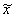 =a'+b'y var tieši aprēķināt no vienādojuma
=a'+b'y var tieši aprēķināt no vienādojuma  =a+bx, un otrādi, algebrisku pārveidojumu ceļā.
=a+bx, un otrādi, algebrisku pārveidojumu ceļā.
3.Ja sakarības ir
korelatīvas, tad abas taisnes krustojas punktā ar koordinātēm 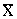 ;
; 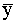 , veidojot leņķi a.
Leņķis a
ir šaurāks, ja sakarības ir ciešākas un otrādi.
, veidojot leņķi a.
Leņķis a
ir šaurāks, ja sakarības ir ciešākas un otrādi.
4.Abas saistītās
regresijas raksturojas ar vienu un to pašu korelācijas koeficientu. Turklāt ir
spēkā sakarība:
r2
= by×x×bx×y,
(9.48)
kur
by×x
un bx×y
ir abu saistīto regresijas vienādojumu
koeficienti. Šo sakarību var izmantot otras saistītās regresijas atrašanai, ja
viena no tām ir zināma.
Ja pazīmju cēloņsakarība nav zināma vai nav
vismaz izteikta darba hipotēze par šādu cēloņsakarību iespēju, abu saistīto
regresijas vienādojumu profesionālās interpretācijas iespējas ir mazas.
Korelācijas un determinācijas koeficientu interpretāciajas iespējas nemazinās,
jo tie ir simetriski pret abām korelatīvi saistītām pazīmēm.
9.6.2. Svarīgākie regresijas un
korelācijas analīzes priekšnoteikumi
Regresijas un korelācijas rādītāju ekonomiskā
interpretācija un pēc izlases datiem aprēķināto rādītāju attiecināšana uz
ģenerālkopu lielā mērā ir atkarīga no sākotnējās informācijas īpatnībām. Tas
pats sakāms par jebkuru citu statistikas rādītāju. Tā, piemēram, aritmētiskais
vidējais labi raksturo pazīmes centrālo tendenci, ja sākotnējie dati veido
simetrisku sadalījumu ar vienu modālo lielumu. Vislabāk, ja sadalījums ir
normāls. Turpretī, ja sākotnējie dati veido multimodālu sadalījumu
(viļņveidīgu, u-veidīgu utt.) vai arī sadalījums nav simetrisks (I-veidīgs),
aritmētiskajam vidējam trūkst dziļākas ekonomiskas jēgas.
Tāpat arī regresijas un korelācijas rādītāju
reālais saturs ir atkarīgs no sāktnējo datu īpašībām. Tādēļ, lietojot
korelācijas un regresijas analīzes metodes, kaut vai aptuveni ir jāzina, kādu
sadalījumu veido apstrādājamās kopas vienības pēc vienas un otras korelatīvi
sastītās pazīmes un kāds ir to kopējais sadalījums. Jānovērtē, vai datu kopā
nav krasi atšķirīgas vienības.
Atkarībā no sākotnējās informācijas īpatnībām,
izšķir divus uzdevumus un līdz ar to modeļu veidus, kuri atšķiras ar
interpretācijas un izmantošanas iespējām.
Pirmais veids atšķiras ar šādām
galvenām īpašībām:
·
darba izpildītāja rīcībā ir zinātniska
teorija vai hipotēze par pētāmo sakarību cēloņsakarību, resp., ir zināms, kura
ir rezultatīvā un kura faktorālā pazīme;
·
faktorālās pazīmes vērtības var noteikt
speciālista brīva izvēle. Tas sevišķi raksturīgi organizētos eksperimentos,
piemēram, pētot mēslojuma ietekmi uz ražību izmēģinājumu lauciņos, tāpat dažādos
inženiertehniskos eksperimentos;
·
neprasa, lai faktorālās pazīmes
sadalījums izlasē reprezentē attiecīgu sadalījumu ģenerālkopā;
·
nav izvirzītas nekādas prasības par
faktorālās pazīmes sadalījumu;
·
ir nepieciešams, lai katrai fiksētai
faktorālās pazīmes x vērtībai atbilstu normāls rezultatīvās pazīmes y
sadalījums;
·
teorētiskie jeb aprēķinātie lielumi
ģenerālkopā atrodas uz regresijas līnijas;
·
ir nepieciešams, lai rezultatīvās pazīmes
y dispersijas visās grupās, kuras izdalītas, grupējot pēc pazīmes x, būtu
aptuveni vienādas.
Ja
sākotnējie dati atbilst šim modelim, tad aprēķinātos sakarību rādītājus var
interpretēt un izmantot šādi:
·
regresijai  =a+bx ir reāla nozīme. Attiecinot to uz ģenerālkopu, pēdējā
jāsaprot kā sastādīta no tādām vienībām, kādas veidoja to kopu, kurai
aprēķināta regresija (izmēģinājuma apstākļi);
=a+bx ir reāla nozīme. Attiecinot to uz ģenerālkopu, pēdējā
jāsaprot kā sastādīta no tādām vienībām, kādas veidoja to kopu, kurai
aprēķināta regresija (izmēģinājuma apstākļi);
·
saistītai regresijai nav reāla satura un
to nevar loģiski interpretēt;
·
korelācijas koeficientam un citiem
sakarību ciešuma rādītājiem ir ierobežota nozīme. To vērtējuma robežas, kas
aprēķinātas ar augstāk minētām metodēm, nav drošas, jo ir atkarīgas no
eksperimentatora izvēlētajām argumenta x vērtībām.
Otrais datu modelis klasiskā vaidā
raksturojas ar šādām īpašībām:
·
teorijas vai hipotēzes par cēloņsakarību
dabu var nebūt. Abus saistītos mainīgos var uzlūkot par cēloniski vienādi
nozīmīgiem;
·
katru kopas vienību iekļauj izlasē,
iepriekš nezinot, kādas ir to x un y vērtības;
·
abi mainīgie lielumi x un y ģenerālkopā
veido divu dimensiju normālu sadalījumu;
·
abu mainīgo lielumu x un y sadalījumi
izlasē raksturo attiecīgos ģenerālkopas sadalījumus.
Šī modeļa gadījumā:
·
abām saistītajām regresijām ir vienlīdz
reāls saturs, un līdz ar to mazas interpretācijas iespējas;
·
visi sakarību rādītāji izlasē raksturo
attiecīgos parametrus ģenerālkopā. Pēdējos var novērtēt, lietojot iepriekš
apskatītās vērtējuma robežu noteikšanas metodes;
·
reāla nozīme ir sakarību ciešuma
rādītājiem; var aprēķināt drošas korelācijas koeficienta vērtējuma robežas. Tie
šajā gadījumā ir galvenie sakarību rādītāji.
Ekonomikas pētījumos diezgan reti var izveidot
kopu, kura bez atrunām atbilst vienam vai otram no aplūkotajiem modeļiem.
Parasti:
·
var izvirzīt teoriju vai hipotēzi par
sakarību cēloņiem (pirmā modeļa pazīme);
·
faktorālo pazīmju vērtības darba
izpildītāji nenoteic brīvi, bet tās rodas izlases rezultātā (otrā modeļa
pazīme);
·
abu pazīmju sadalījumi ir diezgan tuvi
normālajam, bet pēc stingriem pārbaudes kritērijiem pilnīgi tam neatbilst
(otrais modelis ar atrunām).
Tādēļ bieži nākas lietot jauktu modeli. Tādā
gadījumā nosacīti lieto visus sakarību rādītājus, tomēr jāievēro, ka tie ir
aptuveni. Īpaši reālie vērtējumu apgabali var būt plašāki nekā parāda aprēķini.
Tādēļ jāpatur prātā, ka īstie pētījuma rezultāti nav tik precīzi, kā šķietami
parāda sakarību rādītāji. Tādēļ nav nozīmes galīgajos rezultātos uzrādīt vairāk
par 2 - 3 zīmīgajiem cipariem. Tāpat jāseko, lai apskatītie priekšnosacījumi
netiktu rupji pārkāpti, jo tad aprēķinu rezultāti var būt principā nepareizi.
Parasti tas notiek tad, ja izlasē ieslēdz vienu vai vairākas vienības, kas
krasi izdalās no pārējās kopas. Krasi atšķirīgās kopas vienības pirms datu
apstrādes jāizslēdz no kopas. To izdara, vai nu izskatot sākotnējo informāciju
ekspertīzes ceļā, vai izmantojot kādus matemātiskus kritērijus.
Viens no grūti izpildāmiem regresijas -
korelācijas analīzes priekšnoteikumiem ir homoskedativitāte. Tā nozīmē, ka
mainoties faktorālās pazīmes vērtībām nedrīkst sistemātiski mainīties
rezultatīvās pazīmes dispersija (precīzāk - grupu dispersija).
Ja šī prasība nav izpildīta, statistikās kopas
sadalījums ir heteroskedatīvs un mazāk piemērots regresijas analīzei.
Ekonomikas pētījumos ir raksturīgi, ka, pieaugot
faktorālās pazīmes vērtībām, sistemātiski pieaug nevien rezultatīvās pazīmes
vidējā vērtība, bet arī dispersija (variācija).
Mērenu heteroskedativāti praksē parasti ignorē
un aprēķina regresijas modeļus. Ja šī parādība krasi izteikta, var būt
vajadzīgas citas pētīšanas metodes.
Minētajiem priekšnoteikumiem lielu vērību
pievērš matemātiskā statistika, kura ir eksakta zinātne un pretendē uz pilnīgi
precīziem rezultātiem.
Ekonomterija un citas zinātnes, kas izstrādā un
izmanto modeļus, pretendē tikai uz tuvinātiem rezultātiem. Modeļa pamatīpašība
ir tā, ka tas atspoguļo tikai pašas galvenās pētāmā objekta vai parādības
īpašības, bet ne visas. Tādēļ, izstrādājot modeļus ekonometrijā, minētos un vēl
citus priekšnoteikumus tik stingri nepārbauda, kā to paredz matemātiskā
statistika.
Tomēr šie priekšnoteikumi ir jāapzina. To rupja
ignorēšana var novest pie t.s. melu korelācijas, kas var pilnīgi
izkropļot reālo sakarību raksturu.
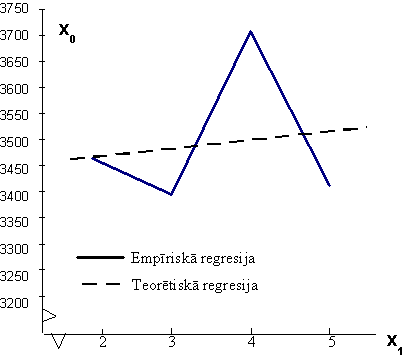
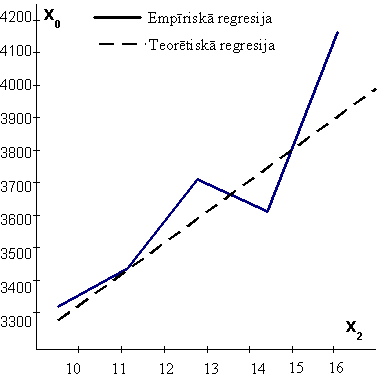
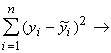 min.
min.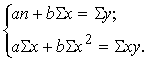
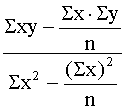 ,
,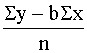 , vai a=
, vai a=
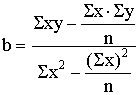 =
=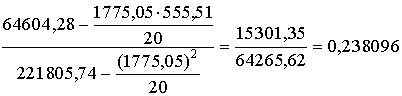 .
.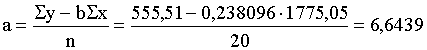 .
.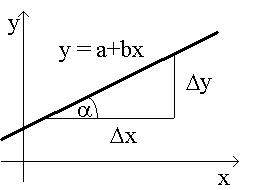
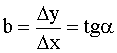 .
.
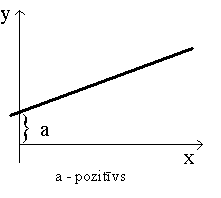



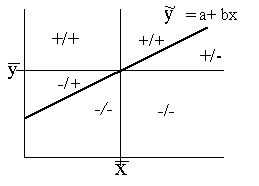
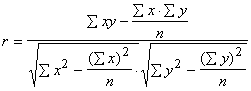 .
.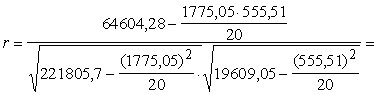
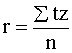 ,
, 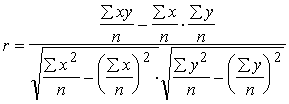 .
.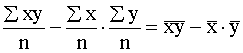
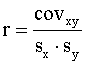 .
. 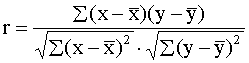 =
=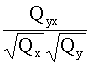 .
.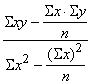
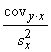
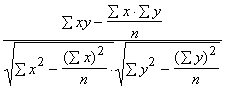
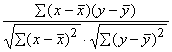
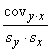
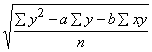
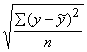
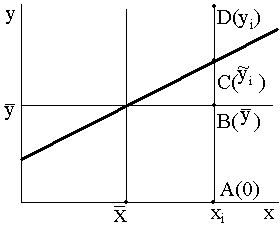
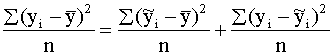 ,
,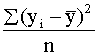 =s2y - visa jeb parastā rezultatīvās
pazīmes dispersija;
=s2y - visa jeb parastā rezultatīvās
pazīmes dispersija;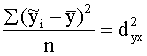
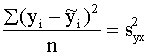
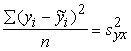 ,
, 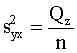 .
. 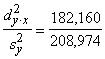 =0,87169.
=0,87169.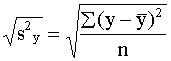 .
.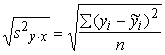

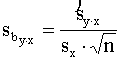 .
.
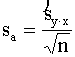 .
. 
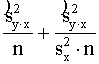 (x -
(x - 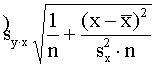 .
.
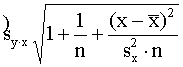 .
.
