11. Daudzfaktoru re­gresija un korelācija

 

11.1. Lineāra  daudzfaktoru  re­gresijas uzdevuma  nostādne  un
         pamatformulas

 

Lai izpētītu kādu interesējošu jautājumu ekonomikā, socioloģijā vai citās rad­niecīgās zinātnēs, reti pietiek aplūkot tikai divas pazīmes un to sakarības, ko var izdarīt ar vienkāršo regresiju un korelāciju. Visbiežāk jautājuma nostādne paredz izmantot vairākas pazīmes, kuras visas saista tādas vai citādas sakarības.

Var izšķirt divas tipveida situācijas.

1.      Pētījumam ir nozīmīga viena faktorālā pazīme, kura lielākā vai mazākā mērā no­saka vairāku rezultatīvo pazīmju veidošanos (to vidējos lielumus).

Tādā gadījumā ir iespējams pētījumu organizēt tā, ka pakāpeniski izpēta un modelē visus ar sakarībām saistīto pazīmju pārus.

Piemēram, dzīves līmeņa pētījumos galvenā faktorālā pazīme ir mājsaimniecības ienākums, rēķinot uz vienu mājsaimniecības locekli. Par rezultatīvajām pazīmēm var uzlūkot dažādu izdevumu grupas: 1) pārtikai, 2) dzīvoklim, 3) apģērbiem un apaviem, 4) zālēm un medicīnai utt. Šādā gadījumā katrai no rezultatīvajām pazīmēm veidojam savu modeli - lineāru vai nelineāru regresijas vienādojumu, par faktorālo pazīmi visu laiku izmantojot mājsaimniecības ienākumus.

2.      Pētījumā ir nozīmīga viena rezultatīvā pazīme, kuru nosaka vairākas faktorālās pazīmes.

Šāda situācija vienmēr izveidojas, modelējot ražošanas procesu, respektīvi izstrādājot ražošanas funkci­jas.

Piemēram, lauksaimniecībā vidējo izslaukumu no vienas govs nosaka dažādu barības līdzekļu patēriņš, rēķinot uz 1 govi: 1) siena, 2) zaļbarības, 3) spēkbarības, kā arī citi ražošanas faktori.

Mēģinājumi arī šīs sakarības sadalīt pa pazīmju pāriem, un šos pārus pētīt un modelēt secīgi, ātri noved pie statistiska paradoksa.

Aprēķinot katram sakarību pārim parasto determinācijas koeficientu un šos koeficientus saskaitot, bieži izrādās, ka summa ir lielāka par 1, respektīvi 100%. Bet vienas un tās pašas rezultatīvās pazīmes variāciju, piemēram, vidējā izslaukuma dažādību saimniecībās, var izskaidrot ar faktorālo pazīmju dažādību vai nu nepilnīgi, vai pilnīgi, bet ne­var izskaidrot vairāk nekā par 100%!

Statistiskā paradoksa cēlonis slēpjas tajā apstāklī, ka arī faktorālās pazīmes nav savā starpā statistiski neatkarīgas, ja arī viņu sakarību cēlonība ne vienmēr ir skaidra.

Piemēram, saimniecībās ar intensīvāku lopkopību govīm izbaro nevien lielākas spēkbarības devas, bet parasti dod arī vairāk siena, sakņu utt. Pētot ar pāru re­gresijas vienādojumu, kā spēkbarības devas ietekmē izslaukumu, spēkbarības pozitīvai ietekmei pieraksta arī citu barības līdzekļu devu pozitīvo līdzietekmi.

Aplūkojot šādas sakarības un to modeļus kopumā, izrādās, ka atsevišķu faktoru ietekme uz rezultatīvo pazīmi ir uztverta atkārtoti. Līdz ar to determinācijas koefi­cientu summa var pārsniegt 1 (100%).

Līdzīgs paradoks ir vērojams arī izmantojot elementārās statistikas pāru sakarību pētīšanas metodes, piemēram, vienkāršos analītiskos grupējumus. Tikai šajā gadījumā grupējumu tabulas nevar tieši "saskaitīt" un parādīt paradoksa esamību. Tomēr viņu interpretācijā ir jāņem vērā viss turpmāk teiktais.

Šādos apstākļos rodas vēlēšanās izpētīt interesējošo faktoru komplekso ietekmi uz rezul­tatīvo pazīmi, novēršot ietekmes dublēšanos, un, ja iespējams, izdalīt katra faktora pat­stāvīgo jeb tīro ietekmi uz rezultatīvo pazīmi ar nosacījumu, ka citu faktoru līdzietekme ir izslēgta. Pilnībā šādu uzdevumu nevar atrisināt, ja faktoru, kas vienlaicīgi ietekmē rezultatīvo pazīmi, ir ļoti daudz. Daļējs atrisinājums ir iespējams. Var pētīt, kā rezultatīvo pazīmi ietekmē galīgs un parasti neliels skaits pašu svarīgāko faktoru. Ja turklāt vēlas izdalīt katra faktora patstāvīgo jeb tīro ietekmi, svarīgs analīzes priekšnoteikums ir, lai pašu faktoru korelatīvās sakarības nebūtu ciešas. Ja šīs sakarības ir ciešas (multikolinearitāte), atsevišķu faktoru patstāvīgo ietekmi nevar izdalīt.

Vairāku faktoru ietekmi uz rezultatīvo pazīmi, faktorus aplūkojot vienkopus, bet izdalot katra ietekmi atsevišķi, ar elementārām metodēm pēta, sastādot kombinētu analītisku grupējumu. Pēc 9.1. tabulas datiem sastādīts kombinēts grupējums ir parādīts 11.1. tabulā.

Tomēr šādi grupējumi ir grūti pārskatāmi, un tajos praktiski nevar izmantot vairāk nekā divas grupēšanas pazīmes (faktorālās pazīmes).

Izmantojot ekonometrijas metodes, vienas rezultatīvās pazīmes atkarību no vairākām faktorālām pazīmēm modelē ar daudzfaktoru regresijas vienādojumu. Šis vienādojums vienkāršākajā gadījumā ir lineārs, sarežģītākos ir vajadzīgs nelineārs vienādojums.

 

11.1. tabula

Siena un spēkbarības patēriņa ietekme uz vidējo izslaukumu no 1 govs
(tabulas centrālās daļas rūtiņās - vidējais izslaukums kilogrammos; kombinēts analītisks grupējums)

 

	Siena patēriņš, rēķinot uz 1 govi	Grupas numurs un spēkbarības patēriņš, rēķinot uz 1 govi gadā, simtos barības vienību					Vidējais izslaukums pa
Grupas	gadā, simtos	1	2	3	4	5	grupām un visās
numurs	barības vienību X1	9.01 - 10.5	10.51 - 12.0	12.01 - 13.5	13.51 - 15.0	15.01 - 16.5	saimniecībās X0
1.	2.01 - 3.0	3324	-	3600	3600	-	3462
2.	3.01 - 4.0	3128	3381	3706	-	-	3393
3.	4.01 - 5.0	3594	3548	3940	3618	4160	3705
4.	5.01 - 6.0	3228	-	3594	-	-	3411
	Vidējais izslau-kums pa grupām un visās saim-niecībās X0	3320	3437	3710	3613	4160	3534

 

Šajā nodaļā aplūkosim lineāru vairāku faktoru regresijas vienādojumu, sākumā aprobežo­joties ar tā vienkāršāko gadījumu, ja vienādojumā ir tikai divas faktorālās pazīmes.

Triju mainīgu lielumu korelācijas diagrammu var izveidot trīs dimensiju telpā. Šajā nolūkā uz horizontālajām asīm atliek divu faktorālo pazīmju skalas, bet uz vertikālās ass - rezultatīvās pazīmes skalu. Punktus telpā atliek atbilstoši trim savstarpēji saistītiem datiem par katru kopas vienību.

Ja ir izveidota korelācijas diagramma telpā, tālākais uzdevums ir atrast virsmu, kura atrastos vistuvāk visām atzīmēm diagrammā. Ja sakarības ir lineāras, tad šāda vir­sma ir plakne. Algebras valodā šāds uzdevums nozīmē atrast meklējamās plaknes vienādojumu.

Funkcionālu sakarību gadījumā visi punkti korelācijas diagrammā atradīsies uz mek­lējamās plaknes. Ja sakarību starp faktorālajām un rezultatīvo pazīmi nav, meklējamā plakne ir paralēla horizontālai (faktoru) plaknei un punkti ap to izvietoti pilnīgi haotiski. Ja sakarības ir korelatīvas, meklējamā plakne ir novietota slīpi pret faktoru plakni. Tās leņķis pret x₁ asi atspoguļo rezultatīvās pazīmes x₀ vidējo lielumu izmaiņu, mainoties faktoram x₁, bet leņķis pret x₂ asi - x₀ vidējo lielumu izmaiņu, mainoties x₂. Punkti grupējas abās pusēs plaknei.

Trīs dimensiju telpiskā attēla projekciju var izveidot plaknē uz papīra lapas, tomēr nolasījumi no skalām šādā gadījumā nav precīzi. Tādēļ tādam attēlam ir vienīgi ilustratīva nozīme. (11.1. attēls)

Četru vai vairāku mainīgu lielumu korelācijas diagrammas nevar izveidot, jo reāli neeksistē četru un vairāku dimensiju telpa. Tomēr no iepriekšējā izrietošos loģiskos un matemātiskos secinājumus var attiecināt arī uz vairāku faktoru sakarībām ar vienu rezultatīvo pazīmi.

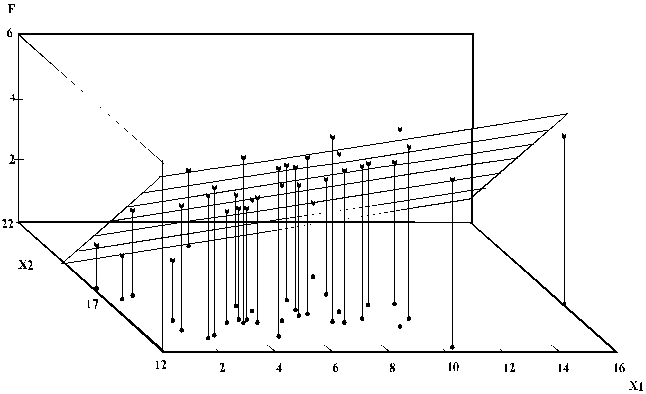
11.1 attēls. Trīsdimensiju korelācijas diagrammas un regresijas plaknes projekcija

 

 

Lineārs daudzfaktoru regresijas vienādojums modelē rezultatīvās pazīmes x₀ atkarību no vairākiem faktoriem x₁; x₂; …; x_k. Trīs mainīgu lielumu, no kuriem divi ir faktorālie, regresijas vienādojumu vienkāršoti pieraksta šādi:

 

 = a+b₁x₁ + b₂x₂ .                                                               (11.1)

 

Ja vajag atsaukties uz vairāku vienādojumu atsevišķiem locekļiem, jālieto sarežģītāks, bet precīzāks pieraksts, lai būtu pilnīgi skaidrs, no kāda vienādojuma, katrs loceklis ņemts. Tad pierakstu veido šādi:

 = a_0.12+b_01.2x₁ + b_02.1x₂ .                                                 (11.2)

 

Regresijas koeficienti ģeometriski nozīmē leņķu tangensus, kurus regresijas plakne veido ar faktoru asīm. Nolasījumi jāizdara uz asīm, nevis ar leņķmēru, jo mainīgo skalas parasti ir dažādas.

Vienādojumu neierobežotam faktoru skaitam vienkāršoti pieraksta šādi:

 

.                                                   (11.3)

 

Vienā daudzfaktoru regresijas vienādojumā var būt tikai viens atkarīgais mainīgais lielums (rezultatīvā pazīme), bet vairāki neatkarīgie mainīgie lielumi (faktorālās pazīmes). Ekonometrijas praksē nākas aprobežoties ar 2 - 6, retāk 8 - 10 faktoriem. Lai izmantotu vairāk faktoru, strauji jāpalielina apstrādājamo datu masīvs, jo pretējā gadījumā atsevišķu regresijas koeficientu statistiskā nozīmība iznāk ļoti zema.

Tāpat kā vienkāršam, arī daudzfaktoru regresijas vienādojumam ir noteikts eksistences apgabals. To parasti ierobežo ar sākotnējos datos sastopamajām faktorālo pazīmju minimālajām un maksimālajām vērtībām un pieraksta ar vairāku dubultnevienādību sistēmu.

Daudzfaktoru regresijas vienādojuma parametrus a, b₁, b₂ …, tāpat kā vienkāršā regresijas vienādojuma parametrus, parasti aprēķina ar vismazāko kvadrātu metodi.

Tas nozīmē, ka tiek izvirzīta prasība

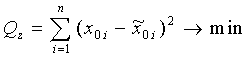,                                             (11.4)

kur:         Q_z -      atlikusī jeb neizskaidrotā noviržu kvadrātu summa;
                        x_0.i -     rezultatīvās pazīmes faktiskā vērtība i-tajā novērojumā;

 -    rezultatīvās pazīmes pēc regresijas vienādojuma aprēķinātā vērtība i-tajam
                         novērojumam (kopas vienībai);

            n  -       novērojumu (kopas vienību) skaits.

 

Ievietojot izteiksmē (11.4)  vietā regresijas vienādojuma (11.3) labo pusi, ņemot visiem parametriem a, b₁, b₂, …, b_k atbilstošos parciālos atvasinājumus, pielīdzinot tos nullēm un apvienojot sistēmā, pēc tās vienkāršošanas iegūstam normālvienādojumu sistēmu daudzfaktoru regresijas vienādojuma parametru a, b₁, b₂ …, b_k aprēķināšanai.

 

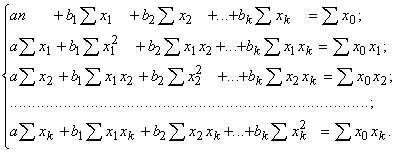                                    (11.5)

Lai pārietu no normālvienādojumu sistēmas vispārīgā pieraksta uz konkrētu uzdevumu, lie­lumi n; Sx₁; Sx₂; …; Sx₀x_k jāaizstāj ar skaitļiem, ko aprēķina pēc konkrēta novērojuma vai eksperimenta datiem. Šos skaitļus ekonometrijas literatūrā sauc par krossummām. Mūsdienās tās aprēķina ar datoru, izmantojot speciālu pro­grammu.

Normālvienādojumu sistēma jāatrisina par nezināmiem lielumiem uzlūkojot a, b₁, b₂ …, b_k. Atrisinājums  dod  vienādojuma brīvo locekli a un visus vajadzīgos regresijas koeficientus.

Normālvienādojumu sistēmu var atrisināt, izmantojot jebkuru paņēmienu. Atrisinot to ar datoru, ieteicams lietot inversās matricas paņēmienu. Ar programmētās vadības kalkulatoru bez grūtībām var atrast inverso matricu līdz 3´3. Tas nav pats precīzākais un ekonomiskākais paņēmiens, bet dod ļoti vērtīgus starprezultātus, respektīvi, vienādojuma sistēmas koeficientu inverso matricu. To izdevīgi izmantot, vienādojuma parametru izlases kļūdu aprēķināšanai.

Lietojot šo paņēmienu, atrisinājumu var pierakstīt šādi:

X{a, b₁, b₂, ..., b_k}=A^-1b,                                                                     (11.6)

 

   kur       A = 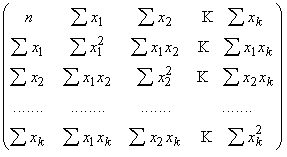                                         (11.7)

 

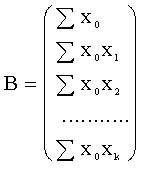.                                                                                   (11.8)

 

 

11.2. Uzdevuma  skaitliska  ilustrācija.

 

Paplašināsim pāru sakarībām veltītajā nodaļā izmantoto piemēru, kurā bija pētīta spēkbarības devu ietekme uz izslaukumu, rēķinot vidēji no 1 govs. Tā kā spēkbarība nav vienīgais barības veids, ko izbaro govīm, un kas ietekmē izslaukumu, iekļausim analīzē otru faktoru - izbarotā siena devas.

Līdz ar to ir jāaprēķina šāda regresijas vienādojuma parametri:

 

,

 

kur:         x₀ - vidējais gada izslaukums no 1 govs, kg;

            x₁  - izbarotā siena daudzums;

x₂ - izbarotās spēkbarības daudzums, abus barības veidus izsakot simtos barības
        vienību uz 1 govi gadā.

 

Siena devas izvirzām kā pirmo faktoru, jo siens ir liellopu bāzes barība ziemas periodā, neskatoties uz to, ka vienas vienības spēkbarības atdeve parasti ir lielāka.

Lai sastādītu un atrisinātu vajadzīgo normālvienādojumu sistēmu, pēc statistikas novērojumiem vai speciāli organizētu zootehnisku izmēģinājumu rezultātiem ir jāaprēķina visas vajadzīgās krossummas. To ir 10.

aprēķinot pēc 9.1. tabulas, tās ir šādas:

 

n=20;                              Sx₁²=333,04;                           Sx₁x₂=962,52;

Sx₀=70483;                    Sx₂²=2960,07;                         Sx₀x₁=281685,2;

Sx₁=79,6;                       Sx₀²=2,49785×10⁸;                   Sx₀x₂=854353,7.

Sx₂=240,5;                    

 

   Šāds uzdevuma apjoms ir maksimālais, ko vēl, pārvarot zināmas grūtības, var izstrādāt ar taustiņu skaitļošanas mašīnām. Izmantojot programmētās vadības kalkulatoru, šo uzde­vumu var atrisināt bez grūtībām.

Ja uzdevums ir lielāks - 3 vai vairāk faktorālās pazīmes - tiklab krossummu aprēķināšana, kā arī normālvienādojumu sistēmas atrisināšana ir jāizdara ar datortehniku.

Šajā gadījumā speciālista galvenais uzdevums ir profesionāli pareizi saprast un interpretēt datortehnikas izdrukas, vispirms - galīgos rezultātus, bet vēlams arī starprezultātus.

Tomēr, iepazīstoties pirmo reizi ar kādu jaunu metodi, ja vien tas vispār iespējams, ir vēlams vismaz vienu uzdevumu atrisināt ar vienkāršākām skaitļošanas mašīnām. Tas dod iespēju labāk izsekot aprēķinu gaitai un to labāk izprast.

Novērtējot piemērā iegūtās krossummas, pievērš uzmanību, ka Sx₀²=2,49785×10⁸ ir ļoti liels skaitlis, ko tiklab datori, kā mazie skaitļotāji parāda normalizētā veidā. Pierakstot šo skaitli parastā veidā, kommats jāpārceļ 8 vietas uz labo pusi, trūkstošos zīmīgos ciparus aizstājot ar nullēm.

Ja grib izvairīties no maziem un ļoti lieliem skaitļiem tiklab starprezultātos, kā arī galīgajos rezultātos, ir jāseko, lai sākotnējie dati veidotu aptuveni vienas kārtas skaitļus.

Piemēram, ja vidējo izslaukumu no vienas govs būtu ņēmuši nevis kilogrammos, bet centneros, tad Sx₀; Sx₀x₁; Sx₀x₂ būtu 100 reizes mazāki skaitļi, bet Sx₀² - 100² = 10000 reizes mazāks skaitlis.

Strādājot ar lineāru modeli, šāda racionāla mērvienību izvēle nodrošina vienīgi darbu ar ērtākiem skaitļiem, bet, izmantojot nelineārus modeļus, mērvienību izvēle var ietekmēt visus darba rezultātus pēc būtības.

Ievietojot piemēra krossummas normālvienādojumu sistēmā, iegūstam:

 

 

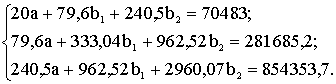
Sistēmas satādīšanas pareizību var pārbaudīt, izmantojot tās simetrijas īpašības (simetrija pa galveno diagonāli).

No skaitļošanas matemātikas viedokļa visām krossummām vajadzētu būt pierakstītām ar vienādu zīmīgo ciparu skaitu, piemēram, ar sešiem. Tas nodrošinātu vismazāko skaitļošanas noapaļojumu kļūdu. Konkrētajā gadījumā tas nav iespējams, ja sākotnējie dati ir pierakstīti ļoti noapaļoti: x₁ un x₂ ar diviem zīmīgiem cipariem. Izdarot saskaitīšanu, Sx₁ un Sx₂ zīmīgo ciparu skaits ir pieaudzis līdz trīs (vairāk nezinam), bet saskaitot šo skaitļu kvadrātus un pāru reizinājumus - līdz seši un septiņi. Noapaļojot visas krossummas līdz trim zīmīgajiem cipariem arī nav lietderīgi, jo tas tomēr pazeminātu aprēķinu precizitāti.

Atrisinot normālvienādojumu sistēmu un rezultātus pierakstot ar lielu zīmīgo ciparu skaitu, iegūstam:

        a = 2202,279;

        b₁ = 39,877933;

        b₂ = 96,728211.

 

Sistēmas atrisinājuma precizitāti var pārbaudīt, ievietojot atrastos parametrus a, b₁, b₂, normālvienādojumu sistēmā attiecīgo burtu vietā. Visām vienādībām teorētiski jāpārvēršas skaitliskās identitātēs. Prakstiski tālākie zīmīgie cipari (parasti sākot ar sep­tīto) atšķirsies noapaļošanas kļūdu rezultātā. Šīs atšķirības var izmantot, lai novērtētu, cik precīzi izpildīts skaitļošanas darbs.

Strādājot ar datortehniku, ir jāpieraksta arī normālvienādojumu sistēmas koeficientu ma­tricas inversā jeb apgrieztā matrica. Tās elementi ļoti atvieglo dažādu izlases kļūdu aprēķināšanu. Piemēram, inversā matrica ir šāda:

 

A^-1.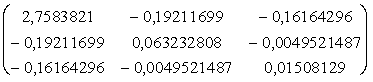

 

Tā kā inversās matricas elementi var būt vajadzīgi tālākos aprēķinos, tie jāpieraksta ar lielu zīmīgo ciparu skaitu, turklāt visi elementi jānoapaļo līdz vienādam zīmīgo ciparu skaitam (piemērā - 8). Nedrīkst noapaļot līdz noteiktam ciparu skaitam aiz komata.

Ja starp krossummām ir ļoti lieli skaitļi, tad atsevišķi inversās matricas elementi būs ļoti mazi skaitļi. Ja no tā grib izvairīties, racionāli jāizvēlas mērvienības sākotnējos datos.

Pārbaudot inverso matricu, jāievēro, ka tās elementiem jābūt simetriskiem pa galveno diagonāli. Uz šīs diagonāles visiem skaitļiem jābūt pozitīviem.

Pareizinot inverso matricu no labās puses ar normālvienādojumu sistēmas brīvo locekļu vektoru, iegūstam sistēmas atrisinājumu.

Novērtējot no skaitļošanas kļūdu uzkrāšanās viedokļa, šis algoritms nav pats labākais, jo prasa izdarīt lielāku skaitu skaitļošanas darbību. Par to var pārliecināties atrisinot normālvienādojumu sistēmu ar dažādām metodēm un rezultātus ievietojot sistēmā a, b₁, b₂ vietā. Skaitliskās identitātes tiks sasniegtas ar atšķirīgu precizitāti.

Tomēr praktiskā ekonometrijas darbā nav vajadzības īpaši noskaidrot, ar kādu metodi strādā dators, jo vajadzīgā galīgo rezultātu precizitāte tiek sasniegta vienmēr.

Līdz šim, pierakstot skaitļošanas starprezultātus un galīgos rezultātus, izmantojām 6 - 8 zīmīgos ciparus, rūpējoties, lai neuzkrājas skaitļošanas kļūdas.

Praktiskai interpretācijai un lietošanai izmantojamos rezultātus daudz vairāk nekā skaitļošanas kļūdas ietekmē sākotnējo datu novērošanas un reģistrācijas kļūdas. Tādēļ galējie rezultāti parasti  ir jānoapaļo līdz 2 -3, retāk 4 zīmīgajiem cipariem.

Pēc tādas parametru noapaļošanas meklētais daudzfaktoru regresijas vienādojums ir šāds:

 

.

 

Bez jau minētajām kļūdām ir jārēķinās vēl ar izlases un modelēšanas kļūdām, par kurām runāsim turpmāk.

 

 

11.3.  Daudzfaktoru  regresijas  vienādojuma  interpretācija

 

11.3.1. Regresijas koeficientu interpretācija

 

Salīdzinot pēc vieniem un tiem pašiem datiem aprēķinātos vienkāršos  un daudzfaktoru regresijas  vienādojumus, var pārliecināties, ka atbilstošo faktoru koeficienti vienmēr atšķiras.

Pētot siena un spēkbarības devu ietekmi uz izslaukumu, tikko kā ieguvām vienādojumu:

 

.

 

Pētot katra faktora ietekmi uz izslaukumu secīgi ar pāru regresijas vienādojumu palīdzību iegūstam:

 

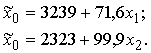
Ja, vadoties no vienkāršā vienādojuma, 100 barības vienību siena nodrošina 71,6 kg papildus izslaukuma, tad, vadoties pēc divu faktoru vienādojuma, tikai 39,9 kg - gandrīz divreiz mazāk. Spēkbarības papildus ietekmes rādītāji abos vienādojumos atšķiras mazāk. Tādēļ ir jāsecina, ka vienkāršo un daudzfaktoru regresijas koeficientu ekonometriskais saturs ir dažāds. (Tāpat kā dažāds saturs un uzdevumi ir vienkāršam un kombinētam analītiskam grupējumam.)

Vienkāršais regresijas koeficients izsaka pētītā faktora nosacīto papildus ietekmi jeb efektivitāti. Nosacītība izpaužas  tajā apstāklī, ka pētītajam faktoram pieraksta visu pārējo faktoru līdzietekmi, kuriem ar  pētīto faktoru ir korelatīvas sakarības. Piemēram, palielinot siena devas par

100 barības vienībām un attiecīgi palielinot spēkbarības devas un pārējos ražošanas faktorus, ir sagaidāms izslaukuma papildus pieaugums par 71,6 kg. Uz to norāda vienkāršais regresijas koeficients.

Daudzfaktoru regresijas koeficients izteiktu pētītā faktora tīro papildus ietekmi jeb efektivitāti, ja vienādojumā būtu ietverti visi faktori, kas ietekmē rezultatīvo pazīmi. Praktiski tas nav iespējams, tādēļ praktiski var izslēgt tikai nedaudzu pašu svarīgāko faktoru līdzietekmi, un daudzfaktoru regresijas koeficients raksturo faktora nosacīti tīro papildus rezultātu jeb efektivitāti. Piemēram, palielinot siena devas par 100 barības vienībām un attiecīgi izmainot pārējos ražošanas faktorus, bet nepalielinot spēkbarības devas, vidējā izslaukuma papildus pieaugums sagaidāms tikai par 39,9 kg. To rāda divu faktoru regresijas vienādojuma koeficients.

Ietverot vienādojumā vēl kādu faktoru, līdzšinējo faktoru papildus ietekmes rādītāju nosacītība samazinās. Tā kā ekonomikā vairumu ražošanas faktoru saista pozitīva korelācija, tālāk samazinās arī attiecīgā faktora regresijas koeficienta skaitliskā vērtība. Par cik kāda faktora ietekme ir vairāk attīrīta no citu faktoru līdzietekmes, par tik šī ietekme ir mazāka.

No ražošanas funkciju teorijas viedokļa regresijas koeficients ir papildus rezultāta jeb robežrezultāta funkcija, kura lineāru sakarību gadījumā ir konstante. Papildus rezultāta funkciju atrod kā sākotnējā modeļa (regresijas vienādojuma) pirmo atvasināto. No tā ceļas termins - robežrezultāta funkcija - papildus rezultāta attiecība pie neierobežoti maza faktorālās pazīmes pieauguma.

Vienkāršo un daudzfaktoru regresijas koeficientu atšķirības matemātiskais cēlonis ir daudzfaktoru vienādojumā ietverto faktoru savstarpējā korelācija. Piemērā siena un spēkbarības devu x₁ un x₂ savstarpējo korelāciju raksturo korelācijas koeficients r₁₂=0,160. Sakarības nav ciešas.

Ideālā gadījumā vismazāko kvadrātu metode paredz, lai vienādojumā ietveramie faktori nebūtu korelatīvi saistīti. Pilnīgas faktoru dekorelācijas gadījumā pāru un daudzfaktoru regresijas koeficienti sakristu. Apstrādājot reālus statistikas datus, to nevar nodrošināt. Tomēr rezultāti ir drošāki, ja faktoru savstarpējā korelācija ir zemāka. Ja tā ir augsta, runā par divu faktoru korelativitāti vai vairāku faktoru multikorelativitāti (arī par kolinearitāti).

Šī paša iemesla dēļ nākas aprobežot daudzfaktoru vienādojumā ieslēdzamo faktoru skaitu, parasti ar 3 - 5, retāk 6 - 10. Cenšoties vēl tālāk palielināt faktoru skaitu, vienādojums kļūst nestabils. Tas nozīmē, ka, aprēķinot šīs pašas sakarības, nedaudz izmainot datu kopu (atmetot vai pievienojot dažas vienības), rezultāti var ievērojami mainīties. Jāsecina, ka sākotnējās informācijas nepietiek, lai pietiekami ticami sadalītu vairāku faktoru komplekso ietekmi pa faktoriem, ņemot tos katru atsevišķi. Lai saglabātu nepieciešmo vienādojumu statistisko nozīmību un stabilitāti, tad palielinot faktoru skaitu, vienlaicīgi vajag palielināt arī izmantojamās informācijas masīvu. Pie tam sākotnējās informācijas masīvam ir jāaug straujāk nekā faktoru skaitam. Ja faktoru savstarpējā korelācija nav augsta, orientējoši var pieņemt, ka kopas vienību skaitam ir jābūt vismaz 10 reizes lielākam nekā faktoru skaitam; labāk, ja 50 un vairāk reizes.

Regresijas koeficientu skaitliskās vērtības ir cieši saistītas ar mainīgo lielumu mērvienībām un vienmēr jāaplūko kopā ar tām. Tādēļ viena vienādojuma dažādu faktoru koeficienti vispārējā gadījumā nav savā starpā tieši salīdzināmi, lai secinātu, kuram faktoram ir lielāka ietekme uz rezultatīvo pazīmi.

Mainot kāda mainīgā lieluma mērvienību, mainās regresijas koeficienti. Piemēram, ja iepriekšējā divu faktoru regresijas vienādojuma rezultatīvo pazīmi x₀ (izslaukumu no govs) izsakām nevis kilogramos, bet centneros, visa vienādojuma labā puse ir jādala ar 100, jo teorētiskiem izslaukumiem jābūt 100 reizes mazākiem. Iegūstam:

 

.

 

 

 

Ja izslaukumu atstājam kilogramos un kilogramos barības vienību izsakām otro faktoru (spēkbarības devas, kuras ir precīzāk dozējamas), ar simtu jādala tikai otrā faktora regresijas koeficients. Iegūstam:

 

.

 

Šoreiz vizuāli izskatās, ka siena devu ietekme uz izslaukumu ir daudz lielāka nekā spēkbarības devu, kaut gan pēc sākotnējā vienādojuma izskatījās otrādi.

Lineārā regresijas vienādojumā manīgo lielumu mērvienības var brīvi mainīt. Ja rezultatīvās pazīmes vienību ņem k reizes sīkāku (lielāku), tad vienādojumā visa labā puse jāreizina (jādala) ar šo skaitli. Ja ņem k reizes sīkāku (lielāku) vienas faktorālās pazīmes vienību, tad attiecīgi jādala (jāreizina) tikai šis regresijas koeficients.

Vienādojumu aprēķinot, mērvienības izvēlas tā, lai visi koeficienti būtu sagaidāmi aptuveni vienas kārtas skaitļi, vismaz robežās no 0,1 - 100. Tas palielina skaitļošanas un izdrukas precizitāti. Vēlamo panāk, pārveidojot sākotnējo informāciju tā, lai visi izmantojamie dati būtu apmēram vienas kārtas skaitļi.

Interpretācijas un izmantošanas stadijā vienādojumu var pārveidot tā, lai visu mainīgo vienības atbilstu tradicionāli statistikā un ekonomikā pieņemtajām. Tas uzlabo rezultātu izpratni. Piemēram, nodrošinājumu ar pamatfondiem tradicionāli izsaka latos vai tūkst. latu, bet ne simtos latu.

 

 

11.3.2. Regresijas koeficientu standartizācija

 

Ja faktori ir dažādi vai dažādas to mērvienības, viena regresijas vienādojuma koeficienti nav savstarpēji salīdzināmi, un pēc tiem nevar pateikt, kurš faktors rezultatīvo pazīmi ietekmē vairāk un kurš mazāk. Lai regresijas koeficientus varētu izmantot šādam nolūkam, tie ir jāpārveido.

Viens no paņēmieniem, kā padarīt salīdzināmus dažādu faktoru ietekmes rādītājus, ir visu mainīgo lielumu standartizēšana. Tas nozīmē, ka visi mainīgie tiek izteikti standartnovirzēs no aritmētiskā vidējā.

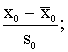
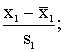
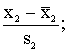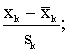……                                 (11.9)

Ja ir aprēķināti parastie regresijas koeficienti un no  tiem jāpāriet uz koeficientiem standartizētā mērgā, lieto formulu:

 

b_j=b_j,                                                                                              (11.10)

 

kur s_j - attiecīgās faktorālās pazīmes, bet s₀ - rezultatīvās pazīmes standartnovirze.

Piemērā s₀=263,827; s₁=0,900888; s₂=1,84469. Līdz ar to:

 

b₁=39,8779.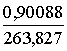=0,13617;

 

b₂=96,7282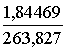=0,67633;

 

 

Apzīmējot ar

 

z_j=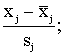j=0,1, …,k,                                             (skat. 11.9)

 

var pierakstīt visu regresijas vienādojumu standartizētā mērogā. Piemērā

 

=0,1362z₁+0,6763z₂.

 

Standartizēto regresijas koeficientu ekonomiskā interpretācija piemērā ir šāda:

·         izmainoties siena devām, rēķinot uz 1 govi par 1 standartnovirzi, papildus izslaukums ir 0,136 standartnovirzes;

·         izmainoties spēkbarības devām, rēķinot uz 1 govi, par 1 standartnovirzi, papildus izslaukums ir 0,676 standartnovirzes.

 

Tā kā standartizētie regresijas koeficienti ir savstarpēji salīdzināmi, var secināt, ka piemēra ietvaros spēkbarības devām ir lielāka ietekme uz izslaukumu nekā siena devām.

Standartizēto regresijas koeficientu nosacītība ir tāda pati kā parasto regresijas koeficientu nosacītība (nosacītie un nosacīti tīrie faktoru papildus ietekmes rādītāji).

Ja pētītie faktori modelī ir salīdzināmi un to mērvienības vienādas, mainīgo standartizācija nav vajadzīga. Piemērā abi faktori ir izteikti barības vienībās, tātad salīdzināmi. Parasto regresijas koeficientu salīdzināšana, ja tā vispār iespējama, balstās uz reālām vienībām un to vidējiem, kamēr standartizētie koeficienti - uz variācijas rādītājiem. Pēdējie ekonomikā tomēr ir mazāk nozīmīgi un mazāk saprotami.

Ja regresijas koeficienti sākotnējās mērvienībās nav aprēķināti un ir vajadzīgi tieši standartizētie koeficienti, pēdējos var aprēķināt, sastādot un atrisinot sekojošu normālvienādojumu sistēmu (divu faktoru gadījumam):

 

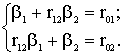                                                     (11.11)

 

Šī ir normālvienādojumu sistēma, kurā izmantoti pāru korelācijas koeficienti. Šīs sistēmas koeficientu matricu sauc par korelācijas matricu un tai ir liela nozīme teorētiskos pētījumos. To izmanto kā sākotnējo informāciju galveno komponentu analīzē, faktoranalīzē u. c., kuras ir vienas no modernajām un samērā sarežģītām daudzdimensiju analīzes metodēm.

Korelācijas matrica vispārējā veidā ir šāda:

 

                                                   (11.12)

 

r_ij=r_ji.

 

Citos gadījumos korelācijas matricā ietver arī pāru korelācijas koeficientus ar rezultatīvo pazīmi t. i. r₀₁; r₀₂; …; r_0k. Tos parasti raksta pirmajā rindiņā un pirmajā kolonā. Tā iegūst t. s. paplašināto korelācijas matricu.

Piemērā (ar paaugstinātu precizitāti):

 

 

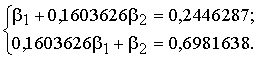
No tās b₁=0,1361711; b₂=0,676327. Ja ir izrēķināti standartizētie regresijas koeficienti, bet darba gaitā vajag parastos, nestandartizētos koeficientus, kuri nav izrēķināti, tos var iegūt ar formulu:

b_j=b_j,                                                                                 (11.13)

 

Piemēram b₂ = 0,6763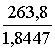 = 96,7, kas sakrīt ar iepriekšējo.

 

 

11.3.3. Parciālā regresija

 

Parciālo regresiju izmanto galvenokārt, lai rastu iespēju attēlot grafiski nosacīti tīrās sakarības.

Šai nolūkā izmanto daudzfaktoru regresijas vienādojumu un fiksē tajā visus faktorus, izņemot vienu - interesējošo - nemainīgā līmenī. Parasti vidējā līmenī.

Pētot, kā izslaukumu ietekmē divu barības veidu patēriņš, ieguvām šādu vienādojumu   = 39,9x₁ + 96,7x₂ + 2202.

 

Zinot, ka             = 3,98,                                = 3524,

                           = 12,0,

 

varam iegūt divus parciālos vienādojumus:

 

= 39,9 × 3,98 + 96,7x₂ + 2202 = 96,7x₂ + 2361  un

= 39,9x₁ + 96,7 × 12+ 2202 = 39,9x₁ + 3362.

 

Tos ērti salīdzināt ar pāru sakarību vienādojumiem:

 

= 71,6x₁ + 3239;

= 99,6x₂ + 2323,

 

un iezīmēt pa divām taisnēm vienā attēlā. Tad viegli izsekot, kā mainījies sakarību modelis, izslēdzot otra faktora līdzietekmi.

 

 

 

 

11.3.4. Daudzfaktoru  regresijas  vienādojuma  lietošana

 

Daudzfaktoru regresijas vienādojumu ekonomikā visbiežāk lieto kā ražošanas funkciju. Tādēļ viņa lietošanas iespējas var noteikt, izmantojot ražošanas funkciju teoriju.

Ja sakarību forma ir lineāra,tad daudzfaktoru regresijas vienādojumu tāpat kā vienkāršo regresijas vienādojumu visbiežāk lieto teorētisko rezultatīvās pazīmes lielumu aprēķināšanai, kas ir saistīti ar noteiktām faktorālo pazīmju vērtībām. Ja ir runa par sakarībām ražošanā, tad tādējādi aprēķinātu lielumu var saukt par ražošanas potenciālu. Tālāk var pētīt šī potenciāla izmantošanu, salīdzinot faktiskos rezultātus ar teorētiskajiem.

Daudzfaktoru modeļus plašākā nozīmē var izmantot, nosakot faktoru samaināmības normas, racionālās faktoru attiecības un pētot dažādus citus jautājumus. Lineāri modeļi gan pēdējiem uzdevumiem izrādās pārāk vienkāršoti. Tādiem pētījumiem ir vajadzīgi nelineāri modeļi, par kuriem runāsim nodaļā par ražošanas funkcijām.

Ražošanas potenciālu konkrētai saimniecībai piemēra ietvaros var aprēķināt vienkārši ievietojot šīs saimniecības faktorālās pazīmes vērtības regresijas vienādojumā.

Pieņemsim, ka kādā saimniecībā, kurai piešķiram ceturto koda numuru, ir izmantotas šādas lopbarības devas: x₁=3,0; x₂=14,6 (siens un spēkbarība simtos barības vienību vidēji uz 1 govi gadā). Izmantojot iepriekš aprēķināto regresijas vienādojumu:

 

 =2202+39,9x₁+0,967x₂,

 aprēķinam

=39,9×3,0+96,7×14,6+2202=3734 (kg).

Tas ir visvarbūtīgākais izslaukums vidēji gadā no vienas govs, dodot faktiski izmantotās barības devas.

Šāds aprēķins ir pareizs, bet nereti psiholoģiski nepietiekoši pārliecinošs. Šaubas rada tas, ka vienādojuma brīvajam loceklim 2202 nav skaidras profesionālas interpretācijas. Līdz ar to tādas nav arī citiem saskaitāmiem aprēķinā. Tādēļ ir lietderīgi pārliecināties, ka ražošanas potenciālu var aprēķināt arī citādi. Aprēķini turklāt ir nedaudz garāki, bet toties visi starprezultāti profesionāli interpretējami. Šajā nolūkā sākotnējo regresijas vienādojumu pieraksta novirzēs no aritmētiskajiem vidējiem. Tāds pieraksts ir iepriekšējā pieraksta identisks pārveidojums. Diviem faktoriem vispārējā veidā tas būs:

bet piemēram

   -3524=39,9(x₁-3,98)+96,7(x₂-12,0),

jeb

   =3524+39,9(x₁-3,98)+96,7(x₂-12,0).

Kā redzams, brīvā locekļa šajā vienādojumā nav; formāli tā vietā nāk rezultatīvās pazīmes (izslaukuma) vidējais aritmētiskais (3524), tātad lielums ar pilnīgi reālu saturu. Potenciālā izslaukuma tālāko aprēķinu ērti sakārtot nelielā tabuliņā. (11.2. tabula)

 

 

 

 

 

 

 

 

 

 

11.2. tabula

 

Noviržu un to ietekmes uz izslaukumu aprēķins 4. saimniecībai

 

	Ražošanas faktoru lielums			Faktora	Sagaidāmā
Ražošanas faktors	4.saimniecībā	Vidēji saimniecību grupā	Novirze + / -	papildus ietekmes (regresijas) koeficients	izslaukuma novirze uz attiecīgā faktora novirzes rēķina, kg
Siens x1	3,0	3,98	- 0,98	39,9	-39
Spēkbarība x2	14,6	12,0	+2,6	96,7	+251
Kopā	x	x	x	x	+212

 

No tabulas redzams, ka 4. saimniecībā, rēķinot vidēji uz govi, ir patērētas 98 barības vienības (0,98 simti jeb centneri barības vienību) siena mazāk nekā vidēji saimniecību grupā. Pareizinot šo novirzi ar siena papildus ietekmes koeficientu 39,9, iegūstam, ka šīs ražošanas faktora negatīvās novirzes rezultātā vidējais izslaukums varēja būt par 39 kg mazāks nekā caurmērā saimniecību grupā. Ceturtajā saimniecībā toties izēdinātas vairāk 260 barības vienības (2,6 simti) spēkbarības. To pareizinot ar papildus ietekmes koeficientu 96,7, iegūstam, ka saimniecībai uz šī faktora pozitīvās novirzes rēķina bija iespējams kāpināt izslaukumu par 251 kg no govs. Rezultātā uz abu faktoru rēķina saimniecības izslaukuma potenciāls ir par 212 kg lielāks nekā vidējais faktiskais izslaukums visā saimniecību grupā (3524 kg). Saskaitot abus pēdējos skaitļus, iegūstam, ka 4. saimniecības izslaukuma potenciāls ir 3736 kg. Aprēķinu gala rezultāts starprezultātu noapaļošanas dēļ var nedaudz atšķirties no rezultāta, ko iegūst ar faktorālo pazīmju vērtību tiešu ievietošanu pamatvienādojumā. Piemērā starpība ir 2 kg, tātad ļoti maza, un to izskaidro starprezultātu dažādi noapaļojumi.

Aprēķināto izslaukuma potenciālu var izmantot kā samērā objektīvu bāzi dažādiem vērtējumiem un prognozēm.

4. saimniecībā faktiskais izslaukums ir 3600 kg. Vidēji saimniecību grupā - 3524 kg. Tātad aplūkojamā saimniecībā faktiskais izslaukums ir par 76 kg jeb par 2,2% augstāks. Saimniecība iegūst pozitīvu vērtējumu. Turpretī, salīdzinot ar izslaukuma potenciālu, faktiskais izslaukums ir nepietiekošs. Veidojas negatīva novirze 136 kg (3600 - 3736), jeb izslaukuma potenciāls ir izmantots tikai par 96,4%.

Jāsecina, ka 4. saimniecība ir panākusi izslaukuma pieaugumu virs vidējā, patērējot ievērojami vairāk spēkbarības, iespējams - iepirktās, nepanākot tās atdevi vidējā līmenī. Pozitīvi jāvērtē saimniecības darbs lopbarības ražošanā, iespējams - sagādē iepērkot, bet negatīvi - šīs lopbarības izmantošanā. Minētie vērtējumi nedrīkst būt kategoriski, jo aprēķinātās novirzes nav lielas.

Novirzes lielumu var novērtēt, salīdzinot to ar vērtējuma standartkļūdu un robežkļūdu. Kā to izdarīt daudzfaktoru analīzes gadījumā, aplūkosim turpmāk.

 

 

11. 4. Daudzfaktoru sakarību ciešuma rādītāji

 

11.4.1. Neizskaidrotā dispersija un vērtējuma standartkļūda

 

Daudzfaktoru regresijas vienādojums, tāpat kā divu mainīgo lielumu regresijas vienādojums, neizsaka funkcionālu, bet korelatīvu sakarību. Tāpēc arī šajā gadījumā ir svarīgi izmērīt sakarību ciešumu, aprēķināt sakarību ciešuma rādītājus.

Tāpat kā vienkāršās regresijas gadījumā, pirms profesionāli interpretējamu rādītāju aprēķināšanas, aprēķina bāzes rādītājus, kuri uzskatāmi par vērtīgiem starprezultātiem. Tie ir :

 

1. neizskaidrotā noviržu kvadrātu summa un

2. neizskaidrotā dispersija.

 

 

Pamatformulas ir analogas vienkāršo pāru sakarību gadījumam. Neizskaidroto dispersiju s²_0.1,2…k jeb vienkāršotā pierakstā s²_z aprēķina ar formulu:

 

,                                                (11.14)

bet tās nenobīdītu vērtējumu ar formulu:

 

.                       (11.15)

 

kur  - ar daudzfaktoru regresijas vienādojumu aprēķinātais jeb teorētiskais rezultatīvās pazīmes lielums.

 

Daudzfaktoru regresijas vērtējuma standartkļūdu aprēķina analogi vienkāršai pāru sakarību vērtējuma standartkļūdai. Vērtējuma standartkļūdu atrod, aprēķinot kvadrātsakni no neizskaidrotās dispersijas:

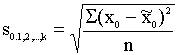,                                                  (11.16)

 

.                                                            (11.17)

 

Formulas (11.14) un (11.15) labi atklāj šo rādītāju loģisko saturu, taču ir maz piemērotas praktiskai lietošanai, jo prasa lielu skaitļošanas darbu. Praksē ieteicams lietot pārveidotas formulas:

-noviržu kvadrātu summu aprēķināšanai:

 

Q_z=S(x₀-)²=Sx²₀-aSx₀-b₁Sx₀x₁-b₂Sx₀x₂-…-b_kSx₀x_k;                      (11.18)

 

- neizskaidrotās dispersijas aprēķināšanai:

 

.           (11.19)

 

Formulu identitāti var pierādīt, izdarot virkni algebrisku pārveidojumu. Formulu (11.18) un (11.19) izmantošanai nepieciešams zināt regresijas parametrus (a, b₁, b₂, …, b_k), un sākotnējo datu krossummas.

Aprēķināsim vērtējuma standartkļūdu agrāk atrastajam regresijas vienādojumam =2202+39,9x­₁+96,7x₂. Vajadzīgās krossummas bija dotas iepriekš. Lai vienkāršotu aprēķinus, mainīsim rezultatīvās pazīmes mērvienību. Dalot rezultatīvās pazīmes datus ar 100, resp., izsakot izslaukumus nevis kilogrammos, bet centneros vajadzīgās krossummas ir šādas:

Sx²₀=24978,476; Sx₀=704,83; Sx₀x₁=2816,852; Sx₀x₂=8543,537; n=20; a=22,0228; b₁=0,398779; b₂=0,967282.

Ievietojot formulā (11.19), iegūstam:

 

;

;

           

;

.

 

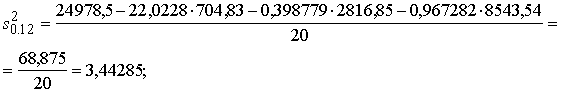
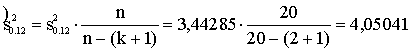Nenobīdītos vērtējumus lieto, ja datus uzlūko par izlasi. Starpība iznāk liela, ja izlase ir maza.

Vērtējuma standartkļūda ir izteikta rezultatīvās pazīmes mērvienībās, pagaidām izslaukuma centneros. To var pārrēķināt arī sākotnējās vienībās kilogrammos, pareizinot ar 100. Piemērā s_0.12=186 kg, kg. To var salīdzināt ar pētītās rezultatīvās pazīmes standartnovirzi s₀=264. Divu pētīto faktoru ietekmes izslēgšanas rezultātā izslaukuma standartnovirze ir samazinājusies par 78 kg (bez korekcijas ar brīvības pakāpju zudumiem). Tomēr atlikusī variācija ir liela. Tas nozīmē, ka bez diviem pētītajiem faktoriem izslaukumu ietekmē vēl virkne citu objektīvu un organizatoriska rakstura faktoru.

Vērtējuma standartkļūdai ir jābūt robežās 0<<s₀. To izmanto aprēķinu rezultātu loģiskai kontrolei, kā arī lai vērtētu, vai faktiskā novirze x₀ -  ir liela, vai maza.

Vērtējuma robežkļūdu atrod vispārējā kārtībā, pareizinot standartkļūdu ar varbūtības koeficientu. Parastā kārtībā atrod arī vērtējuma robežas un apgabalus: robežkļūdu atskaita un pieskaita teorētiskiem līmeņiem.

Robežkļūdas ģeometrisko attēlu var iedomāties kā regresijas plaknei paralēlas plaknes. Reāli to var iedomāties tikai trīs dimensiju telpā.

 

 

11.4.2. Daudzfaktoru determinācijas un korelācijas koeficienti.

 

Daudzfaktoru determinācijas koeficientu aprēķina analogi pāru sakarību determinācijas koeficientam kā izskaidrotās un kopējās dispersiju attiecību. Daudzfaktoru determinācijas koeficients ir daudzfaktoru korelācijas koeficienta kvadrāts.

 

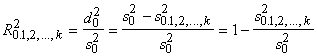.                            (11.20)

Tādēļ daudzfaktoru korelācijas koeficientu aprēķina kā kvadrātsakni no determinācijas koeficienta:

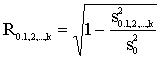.                                                                   (11.21)

 

Daudzfaktoru korelācijas koeficienta īpašības ir līdzīgas vienkāršā korelācijas koeficienta īpašībām tikai daudzfaktoru korelācijas koeficientam neuzrāda algebrisko zīmi, jo vienā regresijas vienādojumā var būt kā pozitīvi, tā negatīvi regresijas koeficienti. Daudzfaktoru korelācijas koeficients var būt skaitlis robežās no 0 līdz 1. Lielāks korelācijas koeficients norāda uz ciešākām sakarībām.

Tā, piemēram, izmantojot regresijas vienādojumu, kurš raksturo divu faktoru ietekmi uz izslaukumu, aprēķinājām, ka neizskaidrotā dispersija ir 3,44285 kopējā dispersija 6,9604.

Tādā gadījumā daudzfaktoru determinācijas koeficients ir:

D = .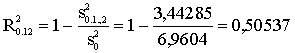

Tas nozīmē, ka dotajos apstākļos apmēram 50% no kopējās izslaukuma dispersijas izskaidro divu aplūkoto faktoru variācija. Pārējos 50 % dispersijas ir izraisījuši citi faktori.

Korelācijas koeficientu atrod, aprēķinot kvadrātsakni no determinācijas koeficienta :

 

.

 

Daudzfaktoru korelācijas koeficients parasti vienmēr ir lielāks par pāru korelācijas koeficientiem, kuri izsaka šīs pašas rezultatīvās pazīmes un faktoru sakarību ciešumu, ņemot faktorus atsevišķi. Reti izņēmumi ir iespējami tad, ja sakarību ciešuma rādītājus aprēķina, ņemot vērā brīvības pakāpju skaita zudumus. Ja sakarību ciešums ir ļoti mazs, tad brīvības pakāpju skaita zudums, kas ir saistīts ar jauna faktora pievienošanu modelim, var vairāk samazināt sakarību ciešuma rādītājus nekā tie pieaug šī faktora reālās ietekmes rezultātā.

 

 

11.4.3 Parciālās korelācijas koeficienti

 

Parciālās korelācijas uzdevums ir noteikt sakarību ciešumu starp rezultatīvo pazīmi un pētījamo faktoru ar nosacījumu, ka dažu citu faktoru līdzietekme ir izslēgta. Parciālo korelācijas koeficientu visvieglāk saprast, ja to izsaka kā korelācijas attiecību. Tā, piemēram, ja pētām pirmā faktora ietekmi uz rezultatīvo pazīmi x₀, otrā un trešā faktora līdzietekme ir izslēgta, tad parciālā korelācijas koeficienta formula ir šāda:

 

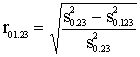.                                                (11.22)

 

Zemsaknes izteiksmes skaitītājā ir divu neizskaidroto dispersiju starpība. s²_0.23 ir dispersija, ko neizskaidro otrais un trešais faktors. s²_0.123 ir dispersija, ko neizskaidro visi trīs faktori. Starpība tātad ir dispersija, ko izskaidro pirmais faktors. Šo dispersiju attiecina pret atlikušo dispersiju, kuru neizskaidro izslēdzamie otrais un trešais faktors.

Ja s²_0.23 = s²_0.123, tad pētītais faktors nemaz neizskaidro rezultatīvās pazīmes dispersiju ar nosacījumu, ka pārējo faktoru ietekme jau iepriekš izslēgta. Parciālais korelācijas koeficients šādā gadījumā ir nulle. Ja visu faktoru neizskaidrotā dispersija ir nulle s²_0.123=0, tad parciālais korelācijas koeficients ir viens, jo pēdējā faktora pievienošana izskaidro visu atlikušo rezultatīvās pazīmes variāciju. Tātad parciālais korelācijas koeficients nevar būt mazāks par nulli un lielāks par vienu. Tam piemīt visas galvenās vienkāršā kolerācijas koeficienta īpašības.

Formulas praktiskā izmantošana ir sarežģīta, jo, lai aprēķinātu visas vajadzīgās dispersijas, bez pamatvienādojuma ir jāaprēķina visi  t. s. subvienādojumi, kuros ir par vienu faktoru mazāk kā pamatvienādojumā.

Matemātiskajā statistikā aplūko arī virkni citu parciālās korelācijas koeficientu formulu. Arī to lietošana prasa lielu skaitļošanas darbu.

Ja vienādojumā ir 3 vai vairāk faktoru, tad parciālās korelācijas koeficientus praktiski var izskaitļot tikai, izmantojot paplašinātās korelācijas matricas inverso matricu.

Datorprogrammas parasti paredz arī korelācijas un determinācijas koeficientu aprēķināšanu ar matricu algebras formulām. Tās vieglāk programmēt, izmantojot gatavus matricu algebras blokus.

 

 

11.5. Daudzfaktoru regresijas un korelācijas izlases kļūdas

 

11.5.1. Daudzfaktoru regresijas koeficienta standartkļūda un robežkļūda

 

Daudzfaktoru regresijas koeficienta standartkļūdas kvadrāta aprēķināšanas pamatformula ir šāda:

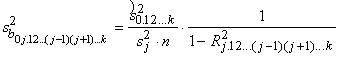.                      (11.23)

Salīdzinot ar vienkāršā pāru regresijas koeficienta standartkļūdas kvadrātu: 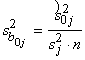 galvenā atšķirība ir reizinātājs .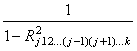

 

Korelācijas koeficients R_{j.12…(j-1)(j+1)…k} raksturo tā faktora, kura regresijas koeficientu pētījām (ar numuru j), sakarību ciešumu ar visiem pārējiem vienādojumā ietvertajiem faktoriem. Aprēķinot šo koeficientu, faktors ar numuru j nosacīti izvirzīts par rezultatīvo pazīmi. Korelācijas koeficientu var aprēķināt ar parastajām daudzfaktoru korelācijas koeficientu aprēķināšanas formulām.

Ja daudzfaktoru regresijas vienādojumā ietvertie faktori būtu savstarpēji neatkarīgi, tad daudzfaktoru regresijas koeficienta standartkļūdas aprēķins būtu analogs ar vienkāršā lineārā regresijas koeficienta standartkļūdas aprēķinu. Tikai neizskaidrotā dispersija  jāaprēķina, vadoties no daudzfaktoru vienādojuma.

Praktiski ekonomikas pētījumos apskatāmie faktori vienmēr ir vairāk vai mazāk korelatīvi saistīti. Tādā gadījumā nevar tik noteikti pateikt, kādā mērā katrs faktors ietekmē rezultatīvo pazīmi. Jo faktoru korelatīvā saistība ir ciešāka, jo spriedums par to patstāvīgo kvantitātīvo ietekmi uz rezultatīvo pazīmi ir nenoteiktāks un otrādi. Šo faktu vajag atspoguļot regresijas koeficientu kļūdu rādītājos. Tādēļ daudzfaktoru regresijas koeficientu standartkļūdas formulā ir speciāls reizinātājs, kas kļūdu palielina tajā gadījumā, ja aplūkojamie faktori ir savstarpēji korelatīvi sastīti.

No formulas redzam, ka gadījumā, ja j-tais faktors ar pārējiem faktoriem nav korelatīvi sastīts, regresijas koeficienta standartkļūda ir minimāla. Tā ir pat mazāka nekā vienkāršā lineārā regresijas koeficienta standartkļūda, jo  . Otrā robežgadījumā, ja j-tais faktors ir funkcionālā sakarībā ar pārējiem faktoriem, tad papildus reizinātāja saucējs kļūst nulle, līdz ar ko standartkļūda (resp., tās kvadrāts) tiecas uz bezgalību. Ja divi vai vairāki faktori ir funkcionāli atkarīgi, ar statistikas metodēm nevar noteikt, kurš no tiem ietekmē rezultatīvo pazīmi un kurš nē.

Aprēķināsim iepriekšējā piemēra regresijas koeficientu standarkļūdas. Ērtības labā rezultatīvo pazīmi - izslaukumu izsakām centneros. Tad b₁=0,398780; b₂=0,967281; =4,05041; s²₁=0,811600; s₂²=3,40288; r₁₂=0,160363.

 

;

.

 

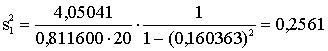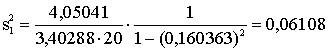Formulu praktiski var izmantot tikai tad, ja vienādojumā ir divi faktori, līdz ar ko formulā ietilpstošais daudzfaktoru korelācijas koeficients kļūst par abu faktoru savstarpējās korelācijas koeficientu r₁₂. Ja faktoru ir vairāk, šīs formulas praktiskā lietošana ir ļoti sarežģīta. Katra regresijas koeficienta standarkļūdas aprēķināšanai jāizskaitļo savs daudzfaktoru korelācijas koeficients. Tad vieglāk izmantot pārveidotu formulu, kura satur normālvienādojumu sistēmas koeficientu inversās matricas diagonālelementu. Aprēķinot vienu reizi inverso matricu, bez pūlēm var aprēķināt visas interesējošo koeficientu standartkļūdas. Tad regresijas koeficientu standarkļūdu aprēķināšana ir ļoti vienkārša. Formula ar vienkāršotiem indeksiem ir šāda:

 

,                                                 (11.24)

 

kur c_jj - inversās matricas attiecīgais diagonālelements.

Piemērā s²_b1=4,05041×0,0632328=0,25612;                                                                             s²_b2=4,05041×0,0150813=0,061085;

aprēķinot kvadrātsaknes s_b1=0,5061, s_b2=0,2472. Ja rezultatīvo pazīmi atkal grib izteikt kilogrammos, šie skaitļi jāpareizina ar 100.

Robežkļūdas aprēķina līdzīgi pāru regresijas gadījumam, pareizinot standarkļūdu ar t koeficientu, kurš atbilst izvēlētai varbūtībai.

Šos lielumus pieskaitot un atskaitot no regresijas koeficientu vērtības, dabūjam koeficientu vērtējumu robežas.

 

11.5.2 Regresijas un indivuduālo vērtējumu izlases kļūdas

 

Daudzfaktoru regresijai, tāpat kā vienkāršai regresijai var aprēķināt pašas regresijas resp. tās vienādojuma un individuālo vērtējumu standartkļūdas. Parastais paņēmiens, saskaitot visu regresijas parametru standartkļūdu kvadrātus, dod formulu, kuru nevar praktiski izmantot tās sarežģītības dēļ. Tādēļ vajadzīgās formulas izstrādā, izmantojot normālvienādojuma sistēmas koeficientu inverso matricu. Aprēķinus praktiski var veikt tikai ar datoru. Šīs metodes parastos matemātiskās statistikas un ekonometrijas kursos neietilpst, un vajadzības gadījumā tās jāmeklē speciālā literatūrā.

 

11.5.3. Nulles hipotēzes pārbaude par regresijas koeficientu

 

Ja pietiek noskaidrot, vai attiecīgais faktors regresijas vienādojumā ir statistiski nozīmīgs, tad pārbauda nulles hipotēzi, kas apgalvo, ka šā faktora regresijas koeficients ģenerālkopā ir nulle. Aprēķina empīrisko t koeficientu kā regresijas koeficienta attiecību pret tā standartkļūdu, salīdzina to ar tabulu t koeficientu robežvērtībām un pieņem lēmumu vispārējā kārtā.

Piemērā (izslaukums kilogrammos):

 

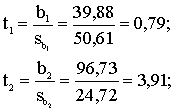
n = 20 - 3 = 17.

Otrais empīriskais t koeficients ir ievērojami lielāks par tabulas vērtību, kas atbilst varbūtībai 0,99. Runājot par pirmo koeficientu, nulles hipotēzi var noraidīt tikai ar varbūtību 0,57, bet nevar noraidīt ar parasti izmantotajām varbūtībām 0,95 vai 0,99. Tātad šī faktora patstāvīga statistiska ietekme nav pierādīta.

 

 

11.5.4. Nulles hipotēze par daudzfaktoru korelācijas koeficientu

 

Šī nulles hipotēze apgalvo, ka korelācijas koeficients ģenerālajā kopā ir nulle. Ja to var noraidīt ar pietiekami augstu varbūtību, tad ir pierādīts, ka pētītās sakarības ir statistiski nozīmīgas.

Šajā nolūkā vislabāk aprēķināt F attiecību un to salīdzināt ar robežvērtībām F - tabulās, kā to dara dispersijas analīzē.

 

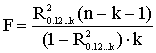.                                            (11.25)

 

Piemērā R²_0.12=0,50537; k=2; n=20.

Līdz ar to .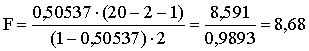

 

Šo lielumu salīdzina ar F  tabulu robežvērtībām. Pēdējo nolasa, izejot no vajadzīgās varbūtības un k un n-k-1 brīvības pakāpēm. Ja izvēlamies varbūtību 0,95 un ņemam vērā, ka izskaidrotai dispersijai n₁ ir k=2 brīvības pakāpes, bet neizskaidrotai n₂=n-k-1=17 brīvības pakāpes, tad F tabulās atrodam, ka

n2\n1­	2
17	3,59

Tā kā F>F_a, nulles hipotēzi noraida. Sakarības kopumā jeb modelis ir statistiski nozīmīgs.

F kritērijs daudzfaktoru analīzē ir nedaudz precīzāks par t kritēriju. T kritērijs ņem vērā tikai vienu (neizskaidrotās) variācijas brīvības pakāpju skaitu. Izskaidrotai variācijai tiek pieņemta viena brīvības pakāpe. F kritērijs ņem vērā kā neizskaidrotās, tā izskaidrotās variācijas brīvības pakāpju skaitu. Citādi F kritērijs ir t kritērija kvadrāts. Pēc matemātiskajām tabulām viegli pārliecināties, ka, piemēram F(a = 0,05; n₁=1) = t² (a = 0,05).

 

 

11.6. Papildjautājumi

 

11.6.1. Normālvienādojumu sistēmas varianti

 

Parādījām, ka daudzfaktoru regresijas vienādojuma koeficienti nemainās, ja rezultatīvo un visas faktorālās pazīmes izsaka novirzēs no aritmētiskajiem vidējiem. Šādam vienādojumam nav brīvā locekļa, resp., a = 0. Tādēļ, piemēram, vienādojuma = a + b₁x₁ + b₂x₂ vietā var tieši aprēķināt vienādojumu ( - ) = b₁(x₁-) + b₂(x₂-). Tas dod iespēju normālvienādojumu sistēmā atrisināmo vienādojumu skaitu samazināt par vienu, kam ir liela nozīme, strādājot ar taustiņu skaitļošanas mašīnām. Lai aprēķinātu minētā vienādojuma koeficientus, ir jāsastāda un jāatrisina šāda normālvienādojumu sistēma:

 

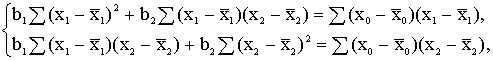resp.:

 

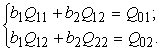                                                                                            (11.26)

 

   Noviržu krossummas no parastajām summām var iegūt ar šādām pārejas formulām:

 

Q_ii = S(x_i - )² =  Sx_i²  -  ;                                                   (11.27)

 

Q_ij  =  S(x_i  -  )(x_j  - )  =  Sx_ix_j  -  .                               (11.28)

 

Lai aizpildītu iepriekšējo normālvienādojumu sistēmu, pirmā formula jāizmanto divas, otra - trīs reizes.

Lai iegūtu regresijas vienādojumu sākotnējās mērvienībās, papildus jāaprēķina vienādojuma brīvais loceklis. To izdara ar formulu:

 

a =  - b₁ - b₂.                                                             (11.29)

 

 

Regresijas koeficienti, kā jau bija minēts, abos vienādojumos ir vienādi. Tādēļ var vajadzības gadījumā izdarīt arī pretēju izmaiņu. Ja ir aprēķināts regresijas vienādojums pazīmēm sākotnējās mērvienībās, tad to var pierakstīt tām pašām pazīmēm arī novirzēs no vidējiem lielumiem, atmetot brīvo locekli.

Dalot iepriekšējās normālvienādojumu sistēmas visus locekļus ar kopas vienību skaitu n, iegūstam trešo normālvienādojumu sistēmu, kura sastādīta, izmantojot kovariācijas un dispersijas:

 

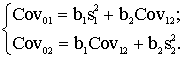                                                              (11.30)

 

Arī  šīs sistēmas atrisinājums dod vajadzīgos regresijas koeficientus b₁ un b₂. Brīvo locekli a var aprēķināt ar agrāk parādīto  formulu.

Pārejas formulas ir šādas:

 

                                                                 (11.31)

 

                                             (11.32)

 

Šī pāreja dod iespēju risināt normālvienādojumu sistēmu ar mazākiem skaitļiem.

Ceturtais normālvienādojumu sistēmas paveids kā matricas elementus satur pāru korelācijas koeficientus. Atrisinājumā iegūst standartizētus regresijas koeficientus.  Tas bija parādīts iepriekš.

11.6. 2. Novērojumu statistiskie svari

 

Parastie korelācijas un regresijas analīzes algoritmi neparedz izmantot statistiskos svarus. Visiem novērojumiem tādā gadījumā it kā piekārto vienu un to pašu svaru f = 1. Visumā tāda rīcība attaisnojas. Zināmas grūtības rodas, ja no korelācijas - regresijas aprēķiniem kā starprezultātus izraksta arī vidējos lielumus. Tā kā tie ir aprēķināti kā vienkāršie vidējie, viņi vairāk vai mazāk atšķiras no tiem vidējiem, kuri saskaņā ar statistikas teoriju ir aprēķināti kā svērtie. Tādēļ rodas jautājums, vai nav mērķtiecīgi arī regresijas vienādojumu un tā raksturotājus aprēķināt, ņemot vērā novērojumu statistiskos svarus. Ir gadījumi, kad vajadzība pēc statistiskajiem svariem regresijas analīzē rodas citu apsvērumu dēļ.

Pirmajā brīdī šķiet, ka statistiskos svarus regresijas analīzes algoritmos varētu iekļaut, vienkārši pareizinot sākotnējos datus ar tiem piekārtotajiem svariem. Tā ka mainīgie lielumi (x₁, x₂ …) regresijas analīzē parasti ir intensitātes relatīvie lielumi, tos pareizinot ar pareizi izvēlētajiem statistiskajiem svariem, iegūst absolūtos lielumus. Piemēram, ja

x - ražība, c/ha,

f - statistiskais svars - sējumu platība ha, tad

z = xf - kopraža.

Tādējādi varam nonākt pie šķietama secinājuma, ka par mainīgajiem jāņem nevis relatīvie, bet absolūtie lielumi. Visumā tāds secinājums nav pareizs. Tas var būt pieņemams vienīgi atsevišķos gadījumos, kad viņu var motivēt profesionālās analīzes ceļā. Piemēram, kad saimniecību lielums raksturo ražošanas koncentrāciju kā faktoru.

Visumā, rēķinot sakarības pēc absolūtajiem lielumiem, aprēķinos iekļūst slēptais faktors - kopas vienību lielums, kas būtiski izkropļo interesējošās sakarības.

Piemēram, pieņemam par

 x - šķirto laulību skaitu rajonā gadā, y - ražotās produkcijas kopvērtību rajonā gadā.

Tad korelācijas diagramma būs aptuveni šāda:

 Iegūsim samērā augstu korelācijas rādītāju   r » 0,9. Katra šķirtā laulība nodrošina lielu produkcijas pieaugumu.

 Ir skaidrs, ka te darīšana ar nepatieso jeb melu korelāciju un statistisko paradoksu.

 Tādēļ, ja regresijas analīzē grib ietvert statistiskos svarus, tie jāpiekārto nevis pašiem datiem, bet noviržu kvadrātiem. Līdz ar to vismazāko kvadrātu metodes kritērijs būs:

 

 

 

 

,                                        (11.33)

 

kur f - katras vienības statistiskais svars.

Izdarot atvasināšanu un citus pārveidojumus, iegūstam normālvienādojumu sistēmu divu mainīgo sakarībām:

 

aSf + bSxf = Syf;                                                                     (11.34)

aSxf + bSx²f = Sxyf;   

 

no kurienes

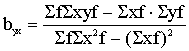;                                                (11.35)

 

 .                                                          (11.36)

 

Triju mainīgo normālvienādojumu sistēmas matrica būs:

 

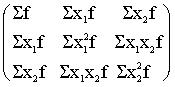,                                                   (11.37)

 

bet brīvo locekļu vektors

 

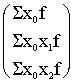.                                                                            (11.38)

 

Tātad visās krossummās statistiskie svari ieiet lineāri, bet netiek kāpināti kvadrātā vai reizināti paši ar sevi, ko iznāk darīt, ja izmanto absolūtos lielumus relatīvo vietā.

Korelācijas diagrammu ar statistiskajiem svariem var iedomāties veidotu no apļiem, kuru lielums ir proporcionāls katra novērojuma svaram.

Regresijas taisne jānovelk tā, lai tā vairāk tuvotos "lielākajiem" apļiem. Apļu centri joprojām sakrīt ar punktiem, kuri būtu atlikti diagrammā, ja svari netiktu ņemti vērā.

Regresijas vienādojums un tā parametri, kuri aprēķināti, izmantojot statistiskos svarus interpretācijas un izmantošanas ziņā neatšķiras no parastajiem.

Tā kā statistiskie svari normālvienādojumu sistēmā ieiet kā visu summējamo skaitļu lineāri reizinātāji, rezultāti nemainās, ja visu svaru sistēmu reizina (dala) ar konstantu skaitli. Šo īpašību plaši lieto, aprēķinot aritmētisko vidējo un citus viendimensijas rādītājus.

Ir lietderīgi šo reizinātāju (dalītāju) izvēlēties tā, lai Sf = n (svaru summa būtu vienāda ar novērojumu skaitu). Tas dod iespēju visus tālākos aprēķinus veikt ar parastajiem algoritmiem un programmām, ieskaitot izlases kļūdu aprēķināšanu.

 

 

11.6. 3. Daudzsoļu regresijas analīze

 

Parasti uzskata, ka daudzfaktoru regresijas vienādojumā lietderīgi ietvert 3 - 10 faktorus. Tāds norādījums ir ļoti nenoteikts un parasti rodas vēlēšanās faktoru skaitu palielināt.

Tomēr daudzu faktoru vienlaicīga ietveršana vienādojumā praktiski saistīta ar lielām grūtībām, kuras rodas galvenokārt sakarā ar faktoru savstarpējo korelāciju.

Rodas jautājums, cik tālu turpināt jaunu faktoru ieslēgšanu vienādojumā, un kad tas kļūst nelietderīgi. Lai atbildētu uz šādu jautājumu, ir jāizvirza noteikti kritēriji, ar kuru palīdzību novērtēt regresijas vienādojuma kvalitāti. Salīdzinot šādus kvalitātes rādītājus vienādojumiem ar dažādu faktoru skaitu, var novērtēt, kurš no tiem ir labāks.

Ir zināmi vairāki vienādojumu kvalitātes rādītāji. Plašāk lieto divus.

Ja vienādojumu paredzēts izmantot galvenokārt rezultatīvās pazīmes teorētisko lielumu aprēķināšanai atsevišķām kopas vienībām, tad par vienādojuma kvalitātes rādītājiem var atzīt sakarību ciešuma rādītājus: vērtējuma standartkļūdu, determinācijas un korelācijas attiecības. Labāks ir tas vienādojums, kuram ir mazāka vērtējuma standartkļūda un lielāka determinācijas un korelācijas attiecība. Ja papildus faktoru ieslēgšanas rezultātā samazinās vērtējuma standartkļūda un palielinās determinācijas un korelācijas attiecības, faktors ir statistiski nozīmīgs. Šo kvalitātes rādītāju uzlabojumam ir jābūt būtiskam jeb nozīmīgam. Niecīgs uzlabojums trešajā vai ceturtajā zīmīgajā ciparā nav ņemams vērā. Vai vienādojuma kvalitātes rādītāji sakarā ar papildus faktora ietveršanu vienādojumā uzlabojas būtiski, vai nē, var precīzi noteikt ar dispersijas analīzes palīdzību, izmantojot F kritēriju. Tā kā šāds aprēķins ir samērā sarežģīts, uzkrājoties zināmai pieredzei, sakarību ciešuma rādītāju starpības nozīmību var novērtēt ekspertīzes ceļā.

Ja vienādojumu grib izmantot ne tikai teorētisko lielumu aprēķināšanai, bet arī lai spriestu par atsevišķu faktoru ietekmes jeb efektivitātes rādītājiem uz rezultatīvo pazīmi, tad ir lietderīgi izmantot citu kritēriju. Vadoties no šī kritērija, par statistiski nozīmīgu atzīst to faktoru, kura regresijas koeficienta attiecība pret šī koeficienta standartkļūdu  pārsniedz iepriekš noteiktu lielumu. Šo kritēriju lieto plašāk.

Ja šī attiecība pārsniedz skaitli 1,96, tad lielas izlases gadījumā faktora nozīmība ir pierādīta ar varbūtību 0,95, ja attiecība pārsniedz 2,58, tad faktora nozīmība ir pierādīta ar varbūtību 0,99. Ja attiecība ir lielāka par 3, faktora nozīmība ir pierādīta ar ļoti augstu varbūtību. Ja faktors pēc sava ekonomiskā satura, tā kvalitatīvajām īpašībām nevarētu būt nenozīmīgs, tad dažreiz to patur vienādojumā arī tad, ja  t koeficients sasniedz vienu. Citiem vārdiem: ja koeficients ir vismaz vienāds ar savu standartkļūdu.

Ja izlase ir maza, tad tabulu kritēriji, ar kuriem salīdzina empīriskos t koeficientus, jāņem no Stjūdenta tabulām.

Papildus faktoru ieslēgšana vienādojumā ir tehniski sarežģītāka. Tādēļ praksē iet pretēju ceļu. Sākumā izvēlas pietiekami daudz faktoru, kuri pēc savām kvalitatīvajām īpašībām varētu ietekmēt rezultatīvo pazīmi (6 - 14 faktorus).

Aprēķina regresijas vienādojumu ar visiem šiem faktoriem. Katram faktoram aprēķina nozīmības rādītāju t_j, kur j - faktora nummurs. Tālāk atrod vismazāko t rādītāju. To salīdzina ar izvēlēto tabulas vērtību. Ja ½t_min½ < t_tab, tad faktors, kuram ir minimālā t nozīme, ir statistiski nenozīmīgs. To no vienādojuma var izslēgt. Maznozīmīga faktora izslēgšanu no regresijas vienādojuma ir vieglāk algoritmizēt nekā papildus faktora ieslēgšanu, kura nozīmība nav zināma. Vieglāk izstrādāt programmas datoram.

Kad vismazāk nozīmīgais faktors ir izslēgts, regresijas vienādojums jāaprēķina no jauna. Līdz ar viena faktora izslēgšanu lielākā vai mazākā mērā mainās vienādojumā atlikušo faktoru regresijas koeficienti.

Ja vienādojumā nevien ½t_min½ < t_tab, bet arī daži citi nozīmības rādītāji ir mazāki par t_tab, uzreiz tomēr var izslēgt tikai vienu faktoru, jo vismazāk nozīmīgā faktora izslēgšana var izraisīt pārējo faktoru nozīmības palielināšanos. Tā rezultātā sākotnējā vienādojumā maznozīmīgi faktori pēc dažu citu faktoru izslēgšanas var kļūt nozīmīgi.

Tādēļ katrā aprēķinu solī izslēdz tikai vienu faktoru, kuram ir minimāls t rādītājs, turklāt mazāks par tabulas vērtību. Kad aprēķināts jaunais vienādojums, kurā ir viens faktors mazāk, procedūra tiek atkārtota. Atkal atrod ½t_min½, - ja tas ir mazāks par t_tab, tad faktoru izslēdz. Tādu aprēķinu procedūru turpina tik ilgi, kamēr visi atlikušie faktori ir statistiski nozīmīgi, par ko liecina tas, ka ½t_min½ > t_tab. Rēķinot ar datoru, šīs operācijas izpilda ciklos jeb soļos. No šejienes rodas nosaukums daudzsoļu daudzfaktoru regresijas analīze.

Ir labi jāizšķir jēdzieni faktora statistiskā un ekonomiskā nozīmība. Ja aprēķini parāda, ka kāds faktors ir statistiski maznozīmīgs vai pat nenozīmīgs, tad tikai retos gadījumos var apgalvot, ka tas ir nenozīmīgs arī no ekonomikas viedokļa. Parasti ekonomiski nozīmīga faktora statistiska nenozīmība rodas faktoru savstarpējās korelācijas, t. s. multikolinearitātes rezultātā.

Vēl apskatīsim gadījumu, kad ar daudzsoļu regresijas analīzi izstrādā nelineāru vienādojumu. Pieņemsim, ka sākotnēji izvēlas vienādojumu

=a+ b₁x₁+ b₂x₂+ b₃x₁²+ b₄x₂²+ b₅x₁x_2.

Ja statistiski nenozīmīgs ir, piemēram, koeficients b₄, un šis loceklis no vienādojuma tiek izslēgts, tad tas vēl nenozīmē, ka statistiski nenozīmīgs ir faktors x₂, jo tas paliek vienādojumā ar locekļiem b₂x₂ un b₅x₁x₂. Locekļa b₄x₂² izslēgšana šādā gadījumā nozīmē vienīgi sakarības formas maiņu tās vienkāršošanas virzienā. Tādēļ daudzsoļu analīze zināmās robežās palīdz meklēt racionālu sakarības formu. Tikai pēdējā locekļa, kas satur, piemēram, x₂, izslēgšana nozīmē paša šī faktora izslēgšanu.

 

 

11.7. Rekomendācijas statistisko sakarību modeļu izveidei

 

11.7. 1. Rezultatīvās pazīmes izvēle

 

Pirms daudzfaktoru regresijas vienādojuma parametra aprēķināšanas ir jāizvēlās un jāpamato rezultatīvā un faktorālās pazīmes, ko ietvert vienādojumā. Izvēli izdara, izmantojot profesionālās zināšanas par pētījamo objektu un sakarību vispārējo raksturu.

Rezultatīvās pazīmes izvēle ir cieši saistīta ar pētījamo problēmu, un tās izvēle parasti grūtības nerada. Izvēloties rezultatīvo pazīmi, vienīgi jāpamato lietderība izmantot korelācijas metodes interesējošo sakarību pētīšanā, kā alternatīvas aplūkojot grupēšanas, indeksu u. c. metodes. Ekonomikas pētījumos par rezultatīvo pazīmi parasti izvēlās tādu, kura daļēji, bet ne tieši un viennozīmīgi atkarīga no cilvēka mērķtiecīgas darbības, kuru bez tam ietekmē arī tieši nekontrolējami dabas, sociāli un bioloģiskie faktori. Piemēram, graudaugu ražība no vienas puses ir atkarīga no lauksaimniecības darbinieku mērķtiecīgas darbības (mēslojuma devas, agrotehnika utt.), bet, no otras puses, no konkrētajiem dabas un klimatiskajiem apstākļiem (tīrumu kvalitāte, nokrišņu daudzums, aktīvās temperatūras utt.). Regresijas vienādojums šādā gadījumā ir modelis, kurš atspoguļo visvarbūtīgāko tieši nekontrolējamo rezultatīvās pazīmes (ražības) lielumu, ņemot vērā iepriekš zināmos faktorus (tīrumu kvalitāti), kā arī tieši maināmus un kontrolējamus faktorus (mēslojumu devas). Tādēļ šāds modelis dod iespēju analizēt un prognozēt sagaidāmo daļēji kontrolējamās parādības lielumu, ņemot vērā veiktos pasākumus.

Nav mērķtiecīgi izvēlēties par rezultatīvo pazīmi regresijas vienādojumam tādas statistiskas pazīmes, kuras atspoguļo tieši vadāmas vai kontrolējamas objekta īpašības vai parādības. - Tās analizē arī citiem, parasti vienkāršākiem paņēmieniem, bet viņu plānošanā var izmantot kādu no optimālās plānošanas metodēm. Ekonometrijā par rezultatīvo pazīmi parasti jāizvēlas relatīvie lielumi, reti absolūtie. Piemēroti ir tiklab naturālie, kā vērtības rādītāji.

 

 

 

 

 

 

 

11.7. 2. Fakotrālo pazīmju izvēle: kvalitatīvās un kvantitatīvās analīzes atbilstība

 

Regresijas modelī par faktoriem ieteicams ieslēgt vienīgi tos, par kuriem no kvalitatīvās jeb profesionālās analīzes rezultātiem ir zināms, ka viņi var cēloniski ietekmēt rezultatīvo pazīmi. Ekonometrija pati par sevi nevar noskaidrot cēloņsakarības. Ja iepriekšējos piemēros mēslojuma devas uzlūkojām par faktoru, bet graudaugu ražību - par rezultātu, tad pamatojums šādai rīcībai ir jāmeklē lauksaimniecības zinātnēs un saimniekošanas praksē. No formāla matemātiskā viedokļa pazīmes varētu arī mainīt vietām, taču tad modelim nebūtu loģiskas interpretācijas un to nevarētu izmantot praksē. Mēs iegūtu t. s. saistīto vienādojumu bez profesionāla satura.

Regresijas vienādojumi, kuri izstrādāti, ignorējot rekomendāciju par kvalitatīvās un kvantitatīvās analīzes atbilstību, no loģikas viedokļa parasti ir absurdi. Ja tomēr mēģina viņus interpretēt, iegūst secinājumus, kurus sauc par nepatieso jeb melu korelāciju (tās pirmais paveids).

Piemēram, angļu statistiķi Dž. Jūls un M. Kendels metodiskos nolūkos ir aprēķinājuši korelāciju starp radioklausītāju skaitu un psihiski slimo skaitu paralēli novietotās dinamikas rindās. Izrādījās, ka abas parādības saista gandrīz funkcionāla sakarība (r = 0,998). Autori jautā: varbūt joka dēļ apgalvot, ka radio klausīšanās gandrīz neizbēgami noved pie psihiskas slimības vai arī tikai trakie klausās radio? Faktiskās bet nepatiesās korelācijas cēlonis te ir zinātnes un tehnikas progress, kura rezultātā arvien plašākiem iedzīvotāju slāņiem kļuva pieejami radiouztvērēji. Tajā pat laikā attīstijās medicīna, kas ļāva konstatēt un ārstēt agrāk ignorētas psihiskas slimības. Tā kā abi procesi norisa paralēli, formāli viņi iznāk cieši korelatīvi saistīti.

Tātad melu korelācijas pirmais paveids var parādīties, ja analīzē nav pamanīts un izmantots kāds svarīgs faktors (piemērā - zinātnes un tehnikas progress), kas vienlaikus ietekmē divas vai vairākas vienādojumā ietvertās pazīmes. Melu korelācijas otru paveidu rada pētījamo pazīmju krasa novirze no normālā sadalījuma (neviendabīga statistiska kopa), kā arī citu regresijas un korelācijas analīzes matemātisko priekšnoteikumu ignorēšana. Tāpat vienību lielums, ja izmanto absolūtos lielumus.

Varam secināt, ka sakarību kvalitatīvā analīze ir jāveic pirms kvantitatīvās analīzes uzsākšanas. Tikai tad, kad ir zināma teorija vai tās vietā izvirzīta saprātīga hipotēze par sakarību kvalitatīvo dabu, cēloņsakarību, ekonometrija kļūst par efektīvu metodi viņu kvantitatīvai izpētei un modelēšanai. Tātad sakarību profesionāla novērtēšana jāveic pirms modeļa parametru aprēķināšanas.

Kvalitatīvās un kvantitatīvās analīzes atbilstība ir jāievēro tiklab pāru kā daudzfaktoru analīzē. (Dažas citas daudzdimensiju metodes, kā galveno komponentu analīze, faktoranalīze, to prasa mazāk).

 

 

11.7.3. Datu metriska samērojamība

 

Regresijas un korelācijas analīze ir kvantitatīvās (skaitliskās) analīzes metode. Tādēļ modelī ietvertajiem faktoriem ir jābūt skaitliski (metriski) samērojamiem. Atributīvu jeb jēdzienisku pazīmju ietveršana modelī, piešķirot to atsevišķām nozīmēm skaitliskus kodus, labus rezultātus nedod. Atributīvu pazīmju piemēri: iedzīvotāju tautības (latvieši, krievi, vācieši utt.), specialitātes (ekonomisti, inženieri, ārsti utt.), laukaugu šķirnes, preču kvalitātes grupas u. c. Šādu pazīmju kodēšana ar sekojošu regresijas analīzi nav pieļaujama tādēļ, ka atsevišķas nozīmes var sakārtot un līdz ar to kodēt dažādi, turklāt starp kodu numuriem nav metriska samēra.

Vienīgais izņēmums šai rekomendācijai ir dinamikas rindu apstrāde, kur laika vienībām (gadiem) piešķir kodus sakārtotas skaitļu rindas veidā. Šāda rīcība ir pieļaujama tādēļ, ka starp aplūkojamiem laika periodiem (gadiem) ir vienāds, tātad metriski samērojams, ilgums. Tomēr arī šajā gadījumā analīzes rezultātiem ir savas īpatnības.

Ja no atributīvām pazīmēm konkrētajā darbā atteikties nevar, lieto citas analīzes metodes (kontingences koeficientus, kovariācijas analīzi u. c.). Ja ir jāpēta tikai atributīvu pazīmju ietekme uz rezultatīvo, efektīva ir grupēšana ar sekojošu dispersijas analīzi. Analizēt vienlaikus kvantitatīvu un atributīvu pazīmju ietekmi iespējams, izmantojot kovariācijas analīzi.

Datu metriska samērojamība kā priekšnoteikums jāievēro, izstrādājot tiklab vienkāršus, kā arī daudzfaktoru regresijas modeļus.

 

 

11.7.4. Faktoru dublēšanās aizliegums

 

Gandrīz katru reālo faktoru var raksturot ar dažādiem statistikas rādītājiem: naturāliem un vērtības, analītiskiem un sintētiskiem, absolūtiem un relatīviem. Piemēram, dotā minerālmēslojuma devas var izteikt fiziskajā svarā vai tīrvielās, var reģistrēt katru mēslojuma veidu atsevišķi, kā arī visus kopā, var novērtēt vērtības izteiksmē utt.

Faktoru dublēšanas aizliegums rekomendē vienā modelī ietvert tikai vienu pazīmi, kas raksturo pētījamo faktoru. Jāizvēlas tā pazīme, kura vislabāk atklāj reālā faktora cēlonisko ietekmi uz rezultatīvo pazīmi. Pazīmes izvēles ziņā visiem gadījumiem derīgu ieteikumu nav.

Ja sakarības ir pietiekami ciešas un stabilas, parasti izvēlās analītiskus rādītājus. Piemēram, kā patstāvīgus faktorus ņem atsevišķi slāpekļa, kālija un fosfora minerālmēslojuma daudzumus. Kopējo daudzumu tādā gadījumā kā jaunu faktoru modelī ietvert nedrīkst.

Ja sakarības ir mazāk ciešas un stabilas, parasti ir jāizmanto sintētiskie rādītāji, piemēram, kopējais visu veidu mēslojuma daudzums, pārrēķinot tīrvielas. Pārejot no analītiskajiem rādītājiem uz sintētiskiem, modeļa stabilitāte parasti uzlabojas, samazinoties tā konkrētībai. To var novērtēt kā specifisku lielā skaita likuma darbību.

Faktoru dublēšanas aizliegums attiecas tikai uz daudzfaktoru modeļiem.

 

 

11.7. 5. Faktoru līdztiesība jeb nepakārtotība

 

Šī rekomendācija iesaka ievērot, lai visi izraudzītie faktori kopējā cēloņsakarību ķēdē atrastos uz viena līmeņa. Citiem vārdiem, nav pieļaujams, ka modelī ietvertie faktori savā starpā ir cēloniski saistīti. Ja šo rekomendāciju ignorē, un modelī kā faktorus ietver tādus, kas pret citiem faktoriem un rezultatīvo pazīmi ieņem starprezultāta stāvokli, tad tālāka analīze parāda, ka statistiski nozīmīgi ir vienīgi faktori - starprezultāti. Sākotnējie jeb primārie faktori kļūst statistiski nenozīmīgi, kas rada šaubas par modeļa pareizību vispār.

Piemēram, rezultatīvā pazīme - lauksaimniecības peļņa vai ienākums uz 1 ha; starprezultatīvās pazīmes - produkcijas vērtība uz 1 ha, svarīgāko produkcijas veidu pašizmaksa; primārie faktori - tīrumu kvalitāte, nodrošinājums ar pamatfondiem un darba spēku utt.

Parasti modelim izvēlās primāros faktorus, jo tieši viņi saimnieciskās vadības gaitā ir maināmi un kontrolējami, lai sasniegtu vēlamo rezultātu. Tādā gadījumā faktori - starprezultāti modelī nedrīkst būt.

Ja kādā uzdevumā tomēr tiek izvēlēti faktori - starprezultāti (tā rīkojas, sastādot vairākus regresijas vienādojumus, kur katrā nākošajā vienādojumā kāds no faktoriem ir iepriekšējā vienādojuma rezultatīvā pazīme), tad jau uzdevuma nostādnes gaitā ir jāatsakās no primāro faktoru ietveršanas konkrētajā vienādojumā.

Faktoru līdztiesība jeb nepakārtotība ir priekšnoteikums, kurš mazāk pieredzējušu analītiķu darbos visbiežāk tiek ignorēts. Tādēļ tam jāpievērš īpaša vērība. Priekšnoteikums attiecās tikai uz daudzfaktoru analīzi. Pāru analīzē var izmantot no šī viedokļa jebkurus faktorus. Tādas analīzes rezultāti bieži atvieglo galīgo izvēli.

 

 

 

11.7. 6. Relatīvo lielumu vienota bāze

 

Ekonomikas pētījumos par rezultatīvo un faktorālajām pazīmēm parasti izvēlās relatīvos lielumus. Absolūto lielumu lietošana aprēķinos ienes "slēpto faktoru"- kopas vienību lielumu, kas lielā mērā izkropļo interesējošās sakarības, visbiežāk fiktīvi palielinot viņu ciešumu vai pat radot melu korelāciju.

Izmantojot par faktoriem relatīvos lielumus, jācenšas, lai visi faktori, kā arī rezultatīvā pazīme būtu pārrēķināti uz vienu ražošanas vienību - bāzi, piemēram, uz 100 ha zemes vai uz vienu strādājošo, vai uz 1000 latiem pamatfondu utt. Tādā gadījumā viegli iedomāties šo faktoru reālo kopdarbību ražošanas procesā, kas atvieglo aprēķinātā vienādojuma parametru ekonomisku interpretāciju. Lietojot relatīvos lielumus, kuriem bāzes ir dažādas (piemēram, dažus pārrēķinot uz 100 ha, citus - uz vienu strādājošo), tādas iespējas zūd, un modelis kļūst nepārskatāms kopumā.

Prakse rāda, ka relatīvo lielumu vienotu bāzi vienmēr nav iespējams saglabāt. Dažos gadījumos šo rekomendāciju var arī neievērot. Tomēr atkāpšanās no viņas apgrūtina rezultātu interpretāciju.

Rekomendācija attiecas tiklab uz pāru kā daudzfaktoru sakarībām. Pāru sakarību gadījumā - uz rezultatīvo un faktorālo pazīmi.

 

 

11.7. 7. Pieļaujamā faktoru savstarpējā korelācija

 

Divus faktorus sauc par lineāri atkarīgiem jeb kolineāriem, ja tos saista funkcionāla lineāra sakarība. Vairāk par divu faktoru lineāru sakarību sauc par multikolinearitāti.

Kolineāru vai multikolineāru faktoru vienlaicīga ietveršana regresijas vienādojumā nav iespējama, jo tas noved pie normālvienādojumu sistēmas, kurai nav atrisinājuma.

Praksē pilnīga kolinearitāte vai multikolinearitāte ir reti sastopama. Toties gandrīz katrā uzdevumā ir jāsastopas ar faktoru savstarpēju korelatīvu sakarību, kuru sauc par daļēju kolinearitāti (multikolinearitāti) jeb korelativitāti (multikorelativitāti). Šādā gadījumā normālvienādojumu sistēmas atrisinājums eksistē, tomēr, palielinoties faktoru korelativitātes ciešumam, zūd gan atrisinājuma precizitāte, gan sevišķi faktoru statistiskā nozīmība. Tādēļ ir svarīgi zināt, kāda faktoru savstarpējā korelācija ir pieļaujama, lai varētu cerēt, ka tie daudzfaktoru vienādojumā būs statistiski nozīmīgi.

Galīgo atbildi uz izvirzīto jautājumu dod daudzsoļu analīze un regresijas parametru novērtēšana ar t - kritēriju. Iepriekšējai novērtēšanai var izmantot šādas nevienādības:

 

r_oi > r_ij,

r_oj > r_ij,

 

kur o - rezultatīvās, i, j - faktorālo pazīmju numuri.

Tas nozīmē, ka faktorus ir lietderīgi ietvert daudzfaktoru modelī, ja viņu vienkāršā korelācija ar rezultatīvo pazīmi ir ciešāka nekā savstarpējā korelācija. Ja šīs nevienādības neizpildās, no kāda faktora ir jāatsakās, kas palielina modeļa nosacītību.

Aplūkotās nevienādības dod iespēju veikt pāru korelācijas matricas iepriekšēju ekspertīzi, kas atvieglo galīgo faktoru izvēli. Tomēr šādas ekspertīzes rezultāti jānovērtē kā darba informācija. Nevienādības nav spēkā nelineāras regresijas gadījumā, kad x_i un x_j ir kādi sākotnējo faktoru matemātiski pārveidojumi, piemēram, x₂ un lnx₂. Korelativitātes problēmas izpēte nelineāras regresijas gadījumā ir sarežģīta un nav ietverama mūsu kursā.

 

 

 

11.7. 8. Sakarību neapgriežamība

 

Iepriekš konstatējām, ka pāru regresija no loģikas viedokļa risina visumā tos pašus uzdevumus, ko vienkārša analītiska grupēšana pēc faktorālās pazīmes. Tā kā statistikā lieto arī grupējumus pēc rezultatīvās pazīmes, ir jānovēro mēģinājumi rēķināt arī atbilstošus regresijas vienādojumus, kur rezultatīvā un faktorālā pazīmes ir formāli mainītas vietām. Šādā gadījumā iegūst t. s. saistīto regresijas vienādojumu, kuram parasti nav ekonometriskas interpretācijas. Sevišķi uzskatāmi tas parādās, ja sakarību ciešums ir mazs. Robežgadījumā, ja r = 0, tātad sakarību nav, parastās regresijas koeficients arī ir nulle. To viegli ekonomiski izskaidrot: ja sakarību nav, nav arī šī faktora ietekmes uz rezultatīvo pazīmi. Citādi tas ir ar saistīto regresijas vienādojumu. Taisnes, kas to attēlo, leņķa koeficients ar x asi, ja r = 0 ir bezgalīgi liels lielums. Iznāk, ka, sakarībām neesot, faktora ietekmes rādītājs tiecas uz bezgalību, kas no ekonomikas viedokļa ir pilnīgi nepieņemami. Tādēļ aprēķināt regresijas vienādojumus, kur par argumentu ņemts atkarīgais mainīgais, bet par funkciju - neatkarīgais, nav pamatoti.

Analītiskajam grupējumam pēc rezultatīvās pazīmes ir ierobežota patstāvīga nozīme, bet matemātiska modeļa, kas būtu šāda grupējuma analogs, nav.

 

 

11.7. 9. Vienkāršības princips

 

Visi nopietni atklājumi zinātnē, pēc tam, kad tie notikuši un pamatoti, izrādās pārsteidzoši vienkārši. Tādēļ jebkurā zinātniskā darbā ir vērojama tieksme pēc vienkāršības. No divām vienlīdz pamatotām teorijām vai hipotēzēm parasti izvēlās vienkāršāko, kurai ir lielākas izredzes attaisnoties turpmākajā pārbaudes gaitā.

Vienkāršības princips īpaši svarīgs modelēšanā. Modeļa uzdevums nav pilnīgi un precīzi kopēt visas modelējamā objekta īpašības. Modeļa jēga ir meklējama tajā apstāklī, ka tas, daudzējādi vienkāršojot sarežģīta vai mazizpētīta objekta īpašības, izceļ pašas galvenās un līdz ar to padara tās skaidrākas un saprotamākas.

Vienkāršības principu izmanto arī izstrādājot daudzfaktoru regresijas modeļus. Sakarā ar šo principu vienādojumā ir jāietver tikai paši svarīgākie faktori, kuri būtiski ietekmē rezultatīvās pazīmes lielumu. No mazsvarīgiem faktoriem ir lietderīgi atsacīties. Modelis ir stabilāks tad, ja tajā mazāk faktoru.

Taču jāatzīmē, ka modelis ar mazāk faktoriem ir abstraktāks nekā modelis, kurā faktoru vairāk. Tādēļ, vadoties no vienkāršības principa nedrīkst nonākt galējībās. Modelī ir jāietver visi faktori, kuri būtiski nosaka rezultatīvās pazīmes lielumu. Ja faktoru ir vairāk - modelis ir konkrētāks, tas satur vairāk informācijas par pētījamām sakarībām.

Vienlaikus ir grūti panākt, lai modelis būtu maksimāli konkrēts un stabils. Šīs īpašības ir savstarpēji konkurējošas. Tādēļ, izvēloties modelī ietveramo faktoru skaitu un sastāvu, ir jāvadās nevien no modelējamo sakarību satura un rakstura (kas ir galvenais), bet arī no pieejamās informācijas apjoma, ticamības un precizitātes, kā arī pētījuma mērķa un uzdevumiem.

Vienkāršības principu ievēro arī izvēloties sakarību formu. Daudz vienkāršāk analizēt modeļus, kuros tikai divi faktori. Īpaši sarežģīti kļūst modeļi, kur kādam faktoram atvēl divus parametrus, piemēram, bx, cx².

 

 

11.7. 10. Sākotnējo datu pareizība un precizitāte

 

Precīzākas pētīšanas metodes parasti prasa precīzākus sākotnējos datus. Darba kopējo precizitāti visumā nosaka visneprecīzākais komponents. Tādēļ, ja ir zināms, ka sākotnējie dati ir nepilnīgi un kļūdaini, var būt nemērķtiecīgi tos apstrādāt ar precīzām ekonometrijas metodēm. Tad var būt lietderīgi aprobežoties ar analītisko grupēšanu, kas parāda sakarību vispārējo raksturu. Sakarību kvantitatīvās īpašības tādā gadījumā vispār nevar izpētīt.

Ekonometrijas lietošana ir lietderīga arī mazāk pilnīgas informācijas gadījumā, ja statistiskā kopa ir liela. Ekonometrijas metodes vislabāk atklāj lielā skaita likuma darbību un var atklāt samērā pareizas sakarības arī tad, ja sākotnējie dati pēc elementāras apstrādes tās nerāda. Jo nepilnīgāki un kļūdaināki dati, jo kļūdu savstarpējai dzēšanai vajag lielākas datu kopas.

Ja ir zināms, ka datu ticamība ir zema, visos gadījumos jāveic pasākumi kļūdu atrašanai un izlabošanai pirms datu apstrādes. Ja kāda novērojuma rezultāti rada nopietnas šaubas, bet atklāt un novērst kļūdu neizdodas, vislabāk šādu novērojumu no tālākās apstrādes izslēgt. Tomēr jāseko, lai izslēgto kopas vienību īpatsvars nepārsniegtu dažus procentus. Ja tādējādi atmet 10 % un vairāk, gala rezultātus var jūtami ietekmēt darba izpildītāja tendenciozs vērtējums, izdarot datu ekspertīzi.