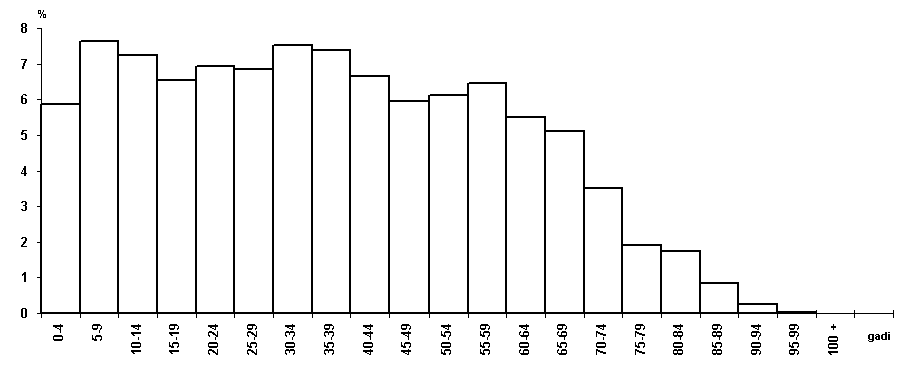
15.1. attēls. Latvijas
iedzīvotāju sadalījums pēc vecuma 1995.g. sākumā, procentos.
15. Neparametriskās statistikas metodes
Ja statistikas datus
grib izmantot kādu likumsakarību noskaidrošanai un lēmumu pieņemšanai, tad
gandrīz vienmēr savāktie dati ir jāuzskata par izlasi no plašākas ģenerālkopas.
Izplatītākās metodes, kuras lieto izlases teorijā un praksē, statistiko
hipotēžu pārbaudē un statistisko lēmumu
pieņemšanā, paredz, ka pētāmā objekta vienības ģenerālkopā pēc interesējošās
pazīmes veido normālu vai tam tuvu sadalījumu. Patiešām liela daļa statistikas
objektu, ar kuriem sastopamies tautsaimniecībā, socioloģijā, preču kvalitātes
pētījumos, inženierzinātnēs u.c., veido normālam tuvu sadalījumu vai tā
modifikāciju - logaritmiski normālu sadalījumu. Tad parastās metodes ir nevien
pamatotas, bet arī efektīvas.
Lai statistikas
vērtējumus un secinājumus padarītu drošākus tajos gadījumos, kad pētāmā objekta
vienību sadalījums būtiski atšķiras no normālā sadalījuma, apmēram no šī
gadsimta vidus, bet īpaši tā pēdējā ceturtdaļā zinātniski ir veltījuši lielas
pūles tādu metožu izstrādei, kuru lietošana neparedz īpašus priekšnoteikumus
par sadalījumu raksturu. Visas šīs metodes kopā veido neparametriskās
statistikas metodes jeb neparametrisko
statistiku.
Ja neparametriskās
metodes saprot plašā nozīmē, tad pie tām pieder arī virkne aprakstošās jeb
empīriskās statistikas metožu un rādītāju, kuri raksturo statistiskā objekta
vienību sadalījumu pēc vienas pazīmes vai vairāku pazīmju sakarības un visbiežāk balstās uz izlases vienību
(novērojumu) ranžēšanu. Te pieder, piemēram, kvantiles (mediāna, kvartiles,
kvintiles, deciles) un pamatojoties uz tām izveidotie rādītāji, rangu
korelācijas koeficienti, kontingences koeficienti u.c.
Par neparametriskās
statistikas metodēm šaurā nozīmē apzīmē specifiskas analītiskās statistikas
metodes, kuras izmanto statistisko hipotēžu pārbaudei, vērtējumu intervālu
noteikšanai un lēmumu pieņemšanai tādos apstākļos, kad pētāmā objekta vienību
sadalījums nav zināms, tātad var būt jebkurš, un īpaši tad, ja ir zināms, ka
tas ievērojami atšķiras no normālā sadalījuma.
Speciālos izdevumos
neparametriskās statistikas metodes aplūko g.k. šaurā izpratnē, vispirms kā
specifiskas statistisko hipotēžu pārbaudes
metodes. Tomēr uzskatījām par lietderīgu šajā darbā ietvert arī dažas
aprakstošās (empīriskās) metodes, kuras var vērtēt kā sagatavošānās posmu, lai
studētu neparametriskās statistikas metodes šaurā nozīmē.
Klasisko jeb
parametrisko statistikas metožu lietošanā ir izveidojušās noteiktas tradīcijas.
Katra raksturīga uzdevuma tipa risināšanai parasti ieteic tikai vienu metodi,
kura vislabāk sevi ir attaisnojusi. Alternatīvas metodes mācību grāmatās
parasti nemaz neuzrāda. Neparametriskajā statistikā turpretīm daudzu uzdevumu
risināšanai piedāvā dažādas metodeas, koeficientus un kritērijus, kuru
savstarpējās priekšrocības un trūkumi ir tikai daļēji noskaidroti. Visbiežāk
šos kritērijus un paņēmienus sauc to izstrādātāju vārdos.
Neparametriskās
statistikas metodes ir saistītas ar daudz un plašu matemātisko (skaitļošanas)
tabulu lietošanu. Tādēļ vajadzīgos gadījumos izmantosim mazus izvilkumus no šim
tabulām, parādot to lietošanu, un uzrādīsim vienu vai divas grāmatas, kurās šīs
tabulas iespiestas samērā pilnīgā veidā.
Šī nodaļa sastāv no
divām daļām.
Pirmā daļā aplūkota
empīrisko datu apstrāde ar neparametriskām metodēm bez rezultātu izvērtēšanas
ar varbūtību teorijas palīdzību. (15.1. iedaļa).
Otrā daļā (tālākās
iedaļas) satur ievadu neparametriskajās statistikas metodēs šaurā nozīmē:
nulles hipotēžu pārbaudi, neparametrisko vērtējumu iegūšanu ar skaitli (punktu)
un ar intervālu raksturīgiem uzdevumu tipiem.
15.1. Variācijas rindas neparametriska
apstrāde
un neparametriski rādītāji
15.1.1. Variācijas rinda un tās
novērtēšana
Savākto statistikas datu apstrādi sāk ar grupēšanu.
Grupējot kopas vienības pēc vienas pazīmes, iegūstam sadalījuma rindu, bet, ja
šī pazīme ir nepārtraukta - intervālu variācijas rindu, kā sadalījumu rindu
paveidu.
15.1. tabula
Latvijas
iedzīvotāju sadalījums pēc vecuma 1995.g. sākumā
|
Vecums, |
Skaits |
Īpatsvars, % |
||
|
gadi |
tiešais |
uzkrātais |
tiešais |
uzkrātais |
|
0 - 4 |
148 220 |
148 220 |
5,86 |
5,86 |
|
5 - 9 |
192 968 |
341 188 |
7,63 |
13,49 |
|
10 - 14 |
183 512 |
524 700 |
7,25 |
20,74 |
|
15 - 19 |
165 484 |
690184 |
6,54 |
27,28 |
|
20 - 24 |
175 024 |
865 208 |
6,92 |
34,20 |
|
25 - 29 |
173 431 |
1 038 639 |
6,85 |
41,05 |
|
30 - 34 |
189 966 |
1 228 605 |
7,51 |
48,56 |
|
35 - 39 |
186 908 |
1 415 513 |
7,39 |
55,95 |
|
40 - 44 |
167 865 |
1 583 378 |
6,64 |
62,59 |
|
45 - 49 |
150 683 |
1 734 061 |
5,96 |
68,55 |
|
50 - 54 |
155 150 |
1 889 211 |
6,13 |
74,68 |
|
55 - 59 |
163 112 |
2 052 323 |
6,45 |
81,13 |
|
60 - 64 |
139 488 |
2 191 811 |
5,51 |
86,64 |
|
65 - 69 |
128 937 |
2 320 748 |
5,10 |
91,74 |
|
70 - 74 |
88 500 |
2 409248 |
3,50 |
95,24 |
|
75 -79 |
48 200 |
2 457448 |
1,91 |
97,15 |
|
80 - 84 |
43 813 |
2 501261 |
1,73 |
98,88 |
|
85 - 89 |
21118 |
2 522 379 |
0,83 |
99,71 |
|
90 - 94 |
6303 |
2 528 682 |
0,25 |
99,96 |
|
95 - 99 |
636 |
2 529 318 |
0,03 |
99,99 |
|
100 un vairāk |
145 |
2 529463 |
0,01 |
100,00 |
|
Kopā |
2 529463 |
- |
100 |
- |
Datu avots: Latvijas demogrāfijas gadagrāmata 1995. - R.: VSK, 1995. - 21.
- 22 lpp.
1.1.
Uzdevums.
15.1. tabulā ir parādīts Latvijas iedzīvotāju sadalījums
pēc vecuma. Jāatzīme, ka demogrāfiskajā statistikā reģistrē pilnus nodzīvotos
gadus, bet nodzīvotos sešus un vairāk mēnešus uz augšu nenoapaļo. Tādēļ
uzrādītie vecuma intervāli īstenībā ir 0 - 4,99; 5 - 9,99 utt. ar centriem 2,5,
7,5 u.t.t. gadi (nevis 2; 7; 12 u.t.t gadi).
Lai labāk uztvertu variācijas rindas raksturu, to attēlo ar histogrammu,
skat. 15.1. attēlu.
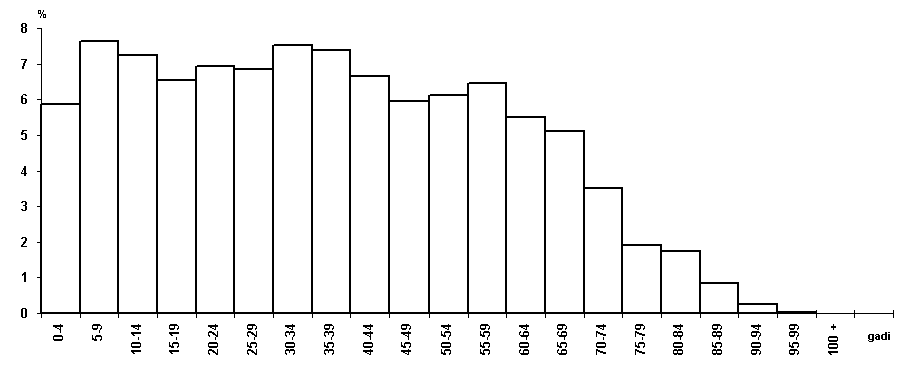
15.1. attēls. Latvijas
iedzīvotāju sadalījums pēc vecuma 1995.g. sākumā, procentos.
Novērtējot šo
sadalījumu, ir redzams, ka tas ļoti būtiski atšķiras no normālā sadalījuma. Nav
viena modālā vecuma intervāla ar vislielāko biežumu, ap kuru koncentrētos citi
intervāli ar lieliem biežumiem. Vāji izteikti ir trīs submodālie intervāli: 5
-15 g., 30 - 35 g. un 55 - 60 g . Ļoti tuvināti vērtējot, no 0 līdz 60 g.
vecumam, iedzīvotāju sadalījums pēc vecuma ir gandrīz vienmērīgs, tālāk -
vienpusēji dilstošs.
Šādam sadalījumam,
tāpat kā iebkuram nepārtraukta lieluma sadalījumam, var izrēķināt parastos
raksturotājus - aritmētisko vidējo, standartnovirzi u.c., bet to saturs ir
ierobežots.
Aritmētiskais
vidējais un standartnovirze ir normālā sadalījuma parametri, no šejienes
termins - parametriskā statistika.
Ja sadalījums ir
tuvs normālam, tad aritmētiskais vidējais rāda sadalījuma centrālo tendenci:
variantu vai intervālu ap kuru grupējas vislielākie biežumi. Latvijas
iedzīvotāju sadalījumam pēc vecuma nekāda centrālā tendence nav vērojama.
Ja aritmētisko
vidējo tomēr izrēķina, var teikt, ka tas raksturo sadalījuma novietojumu uz
skaitļu ass jeb svešvārdā - lokāciju. Ja histogrammu izgatavotu no materiāla ar
zināmu masu, tad punktā, kurš atbilst aritmētiskajam vidējam, atbalstītais
ķermenis varētu saglabāt līdzsvaru. Tāda interpretācija ir mazāk izteiksmīga
nekā normālā sadalījuma gadījumā, kad aritmētiskais vidējais rāda centrālo
tendenci.
Latvijas iedzīvotāju
vidējo vecumu aprēķinājām pēc sīkāka
grupējuma, nekā parādīts 15.1. tabulā. Latvijas demogrāfijas gadagrāmatā 1995.
ir uzrādīts iedzīvotāju skaits vienu gadu
lielos vecuma intervālos no 0 līdz 64.g. vecumam, tālāk izmantojot piecu gadu
lielus intervālos. Pēc šāda grupējuma ieguvām
vidējo iedzīvotāju vecumu 37,33 gadi
ar standartnovirzi 22,42 gadi. Pēc pēdējās 1989.g. tautas skaitīšānas
datiem iedzīvotāju vidējais vecums bija 36,3 gadi. Tas nozīme, ka nepietiekamas
dzimstības rezultātā 1990. - 1995.g. laikā ir notikusi iedzīvotāju novecošanās
par vienu gadu.
Ja kopas vienību
sadalījums krasi atšķiras no normālā sadalījuma, šādu sadalījumu var raksturot
ar neparametriskiem rādītājiem, kuri dažkārt ir izteiksmīgāki nekā
parametriskie.
15.1.2. Mediāna
Rādītājs, kurš
interpretācijas iespēju ziņā var konkurēt ar aritmētisko vidējo, ir mediāna.
Mediānas un daudzu
citu neparametrisko rādītāju aprēķināšana balstās uz kopas vienību sakārtošanu
jeb ranžēšanu pēc aplūkojomās pazīmes.
Pirms aprēķināt
Latvijas iedzīvotāju vecuma mediānu pēc 15.1. tabulas datiem, izmantosim
vienkāršāku piemēru.
1.2. Uzdevums.
Pieņemsim, ka ir
dati par 10 cilvēku vecumu: 5; 37; 4; 74; 40; 22; 27; 14; 1; 31 gads. Ja šos
vecumos (līdz ar to cilvēkus, kā šīs īpašības nesējus) sakārto pazīmes augošā (retāk - dilstošā)
secībā un sanumurē sākot ar vienu, tad piešķirtie kārtas numuri ir rangi (15.2.
tabula).
15.2.
tabula
Kopas
vienību tieša ranžēšana
|
Vecums, gadi |
1 4 5
14 22 27
31 37 40
74 |
|
Rangs |
1. 2. 3.
4. 5. 6.
7. 8. 9.
10. |
Mediāna ir tā
pazīmes nozīme (vecums), kura ranžētu rindu dala uz pusēm: pa abām pusēm no
mediānas ir vienāds novērojumu skaits. Ja kopējais novērojumu skaits ir
nepārskaitlis, mediānu var nolasīt tieši. Ja tas ir pārskaitlis, ņem divu
centrā esošo novērojumu vidējo:
![]() (gadi).
(gadi).
Ja kopas vienību ir
daudz (kā 15.1. tabulā), visu to ranžēšana bez datora nav iespējama un nav arī
vajadzīga. Lai atrastu medianu pēc intervālu variācijas rindas, vispirms ir
jāatrod mediānas intervāls.
Mediānas intervāls
ir tas, kurā uzkrāto biežumu summa (15.1. tabulas 3. aile) pirmo reizi
pārsniedz pusi no visa kopas vienību skaita. Uzdevumā tas ir vecuma intervāls
35 - 39 gadi (1415513 > 2529463:2). Vēl vieglāk mediānas intervālu atrast
pēc uzkrātajiem relatīvajiem biežumiem (5.aile). Mediānas intervāls ir tas
intervāls, kurā uzkrāto relatīvo biežuma summa pirmo reizi pārsniedz 50%.
Pašu mediānu
mediānas intervāla ietvaros atrod ar šādu interpolācijas formulu, pieņemot, ka
vienību sadalījums intervāla ietvaros ir vienmērīgs:
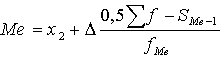 , (15.1)
, (15.1)
kur:
![]() - mediānas (2.kvartiles) intervāla apakšējā
robeža;
- mediānas (2.kvartiles) intervāla apakšējā
robeža;
![]() - mediānas intervāla lielums (garums);
- mediānas intervāla lielums (garums);
![]() - kopējais vienību
skaits variācijas rindā, arī n;
- kopējais vienību
skaits variācijas rindā, arī n;
![]() - uzkrātais biežums
intervālā, kas atrodas pirms mediānas intervāla;
- uzkrātais biežums
intervālā, kas atrodas pirms mediānas intervāla;
![]() - mediānas intervāla
vienību skaits.
- mediānas intervāla
vienību skaits.
Izdarot ievietojums pēc 15.1. tabulas datiem (iedzīvotāju
skaits noapaļots tūkstošos), iegūstam:
![]() .
.
Ja relatīvie biežumi ir uzrādīti ar pietiekami daudziem
zīmīgajiem cīpariem, mediānu var izskaitļot arī pēc tiem:
![]() .
.
Mediānai vienmār
jāatrodas mediānas intervāla ietvaros, piemērā - intervālā no 35 līdz 39,99
gadi.
Tātad Latvijas
iedzīvotāju vecuma mediāna 1995.g. bija gandrīz 36 gadi. Tas nozīmē, ka puse
iedzīvotāju bija jaunāki, bet puse -
vecāki par šo vecumu. Tādējādi mediānai ir skaidra saturiska interpretācija
jebkura sadalījuma gadījumā.
Tā kā mediānu negrupētu datu gadījumā nosaka tikai viena
sakārtotas rindas vidū esošā vienība, bet grupētu datu gadījumā - mediānas
intervāls, mediānas lielumu neietekmē krasi atšķirīgas vienības (artefakti)1,
ja tādas ir statistiskajā kopā.
____________________
1 Krastiņš O. Ievads stabīlo vērtējumu
metodēs. - R.: LVU, 1987. -25 lpp.
Mediānu
tāpat kā visus citus neparametriskos rādītājus var aprēķināt arī tad, ja kopas
sadalījums ir normāls vai tuvs tam. Tādēļ neparametriskie rādītāji ir
universālāki nekā parametriskie.
Tomēr neparametrisko
rādītāju lietošanu parametrisko rādītāju vietā, kad ir pamatoti lietot arī
parametriskos, nevar ieteikt tādēļ, ka neparametriskie rādītāji ir mazāk
efektīvi. Piemēram, lai sasniegtu vienādu izlases kļūdu, rēķinot mediānu, jāņem
1000 vienību, bet, rēķinot aritmētisko vidējo - tikai 637. Atšķirību var
izskaidrot ar to, ka, rēķinot aritmētisko vidējo, ņem vērā katras kopas
vienības tiešo pazīmes vērtību (datu), bet, rēķinot mediānu, - vienīgi šo
vienību vietas ranžētā rindā. Tādēļ daļa derīgās informācijas netiek izmantota.
15.1.3. Neparametriskie struktūras
rādītāji
Arī mediānu var
uzlūkot par struktūras rādītāju, jo tā dala statistisko kopu divās vienādās
daļas. Tomēr ar tik vienkāršu (rupju) dalījumu sadalījuma struktūru kaut cik
pilnīgi raksturot nevar.
Skaitļus, kas
sakārtotu statistisko kopu dala četrās, piecās, desmit, simts vienādās daļās,
sauc par sadalījuma kvantilēm. Sadalījumu četrās daļās dala kvartiles, piecās -
kvintiles, desmit - deciles, simts - centiles jeb procentiles.
Sadalījuma daļas,
grupas, kas atrodas starp divām blakus esošām kvartilēm, sauc par kvartiļu
grupām, starp divām decilēm - par deciļu grupām u.t.t. Visās kvartiļu grupās ir
25% no kopas vienību skaita, deciļu grupās - 10% no kopas vienību skaita utt.
Līdz ar to visas šādi izdalītas grupas
ir vienādi reprezentatīvas.
Kvantiles tāpat kā
mediānu var aprēķināt tieši pēc sākotnējiem datiem, kopas vienības ranžējot.
Tāds paņēmiens dod visprecizākos rezultātus. Ja ir izstrādāts grupējums, atrod
tajā vajadzīgās kvantiles intervālu, bet pašu kvantili izskaitļo ar interpolācijas
formulu. Šis paņēmiens dod tuvinātus rezultātus.
Lai aprēķinātu
kvartiles pēc 15.1. tabulas datiem, atrod pirmo un trešo kvartili saturošos
intervālus. Otrā kvartile vienlaikus ir mediāna, un tā ir jau aprēķināta.
Pirmās kvartiles
intervāls ir tas, kurā uzkrāto relatīvo biežumu summa pirmo reizi pārsniedz
25%. Uzdevumā tas ir intervāls 15 -
19,99 gadi.
Trešās kvartiles
intervāls ir tas, kurā uzkrāto relatīvo biežumu summa pirmo reizi pāsniedz 75%.
Uzdevumā tas ir
intervāls 55 - 59,99 gadi. Pašas kvartiles atrod ar interpolācijas formulām,
kuras ir izveidotas līdzīgi mediānas formulai:
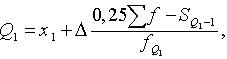 (15.2)
(15.2)
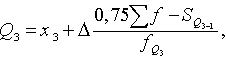 (15.3)
(15.3)
kur:
![]() un
un ![]() - pirmā un trešā kvartile;
- pirmā un trešā kvartile;
![]() un
un ![]() - pirmās un trešās
kvartiles intervāla apakšējā robeža;
- pirmās un trešās
kvartiles intervāla apakšējā robeža;
![]() - kopas vienību
skaits;
- kopas vienību
skaits;
![]() - uzkrātais biežums
intervālā, kas atrodas pirms attiecīgās kvartiles
- uzkrātais biežums
intervālā, kas atrodas pirms attiecīgās kvartiles
intervāla;
![]() - attiecīgās kvartiles
intervāla biežums.
- attiecīgās kvartiles
intervāla biežums.
Pēc 15.1 tabulas datiem var izrēķināt, ka
![]() ,
,
![]() .
.
Tātad 1955.g.
ceturtā daļa Latvijas iedzīvotāju bija jaunāki par 18,26 gadiem un ceturtā daļa
- vecāki par 55,25 gadiem. Ņemot vēl vērā mediānu, visa statistiskā kopa ir
sadalīta pēc biežumiem (vienību skaita) četrās vienādi lielās grupās.
Līdzīgi var
izrēķināt deciles. Vienīgi, ja grib izmantot grupētus datus, izdalīto grupu
skaitam ir jābūt vairāki desmiti.
15.1. tabulā ir
izdalīta 21 grupa. Deciļu grupējumā vajag 10 grupas. Tādēļ, aprēķinot deciles pēc 15.1. tabulas datiem,
lielu īpatsvaru iegūst interpolācija pēc iepriekšējām analogām formulām, kas
samazina deciļu precizitāti. Tādēļ pēdējā laikā statistikas praksē deciles
aprēķina ar datoru, ranžējot tieši sākotnējās kopas vienības. Deciļu grupējumā
nav tik liela nozīme skaitļiem, kas nodala vienu deciles grupu no otras, kā
pašām deciļu grupām.Šim grupām var aprēķināt grupu vidējos un grupu variācijas
rādītājus, pretstatīt vienu grupu otrai u.t.t, iegūstot plašu un vispusīgu
materiālu par kopas sadalījumu. Katrai deciles grupai var aprēķināt arī kādu
citu ar grupēšanas pazīmi saistītu pazīmju vidējos lielumus. Sakārtojot šādu
materiālu tabulā, iegūstot deciļu analītisko grupējumu, kurš tāpat kā parastais
analītiskais grupējums rāda sakarību esamību un raksturu starp grupējumā
ietvertajām pazīmēm (skat. 9.4. tabulu 9. nodaļā).
Aprēķnāsim pirmo un
devīto decili pēc 15.1. tabulas datiem.
Pirmā decile atrodas grupā, kurā uzkrātais
relatīvais biežums pirmo reizi pārsniedz 10%. Uzdevumā tā ir vecuma grupa 5 -
9,99 gadi. Pašu decili šīs grupas ietvaros atrod ar interpolācijas formulu
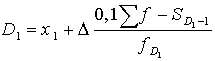 , (15.4)
, (15.4)
kur simboli analogi iepriekšējiem, tikai kvartiļu grupu
vietā deciļu grupas. Uzdevumā
![]() .
.
Devītā decile
atrodas grupā, kur uzkrātais relatīvais biežums pirmo reizi pārsniedz 90%. Uzdevumā tā ir vecuma grupa 65 - 69,99 gadi. Pašu
decili aprēķinam ar interpolācijas formulu
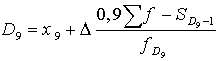 ; (15.5)
; (15.5)
![]() .
.
Iegūtie rezultāti
jānovērtē kā tuvināti. Interpretējot iegūtos rezultātus, var teikt, ka 1995.g.
Latvijā bija 10% iedzīvotāju jaunāki par 7,7 gadiem un 10% vecāki par 68,3
gadiem.
15.1.4. Kvantiļu variācijas rādītāji
Izmantojot kvantiles
(kvartiles, deciles u.c.), var izveidot variācijas rādītājus, kuriem ir
analoģija ar parastajiem parametriskajiem variācijas rādītājiem. Pēdējie
bāzējas uz normālā sadalījuma otro parametru - standartnovirzi.
Par absolūtās
variācijas rādītājiem var izmantot divu kvantiļu (parasti pēdējās un pirmās)
starpību.
Izmantojot kvartiles
![]() (15.6)
(15.6)
uzdevumā Q = 55,25 - 18,26 = 36,99 (gadi).
Izmantojot deciles
![]() , (15.7)
, (15.7)
uzdevumā
D
= 68,29 - 7,69 = 60,60 (gadi).
Interpretējot
iegūtos rezultātus, var secināt ka 50% Latvijas iedzīvotāju vecums variēja 37 gadu robežās (noapaļojot) bet 80% iedzīvotāju - 60,6 gadu robežās.
Ja pieņemtu, ka
minētie rezultāti ir iegūti pēc reprezentatīvas izlases datiem un ģenerāl
-kopas sadalījums ir tāds pat kā izlasei,tas var būt jebkurš, tad uzrādītos
kvantiļu intervālus var saistīt ar noteiktām varbūtībām.
Varbūtība, ka
nejauši no ģenerālkopas ņemta vienība nonāks intervālā ![]() ir 0,5, bet intervālā
ir 0,5, bet intervālā ![]() .
.
Kā kvantiļu vidējo
novirzi var izmantot pusi no kvantiļu intervāla:
![]() ; (15.8)
; (15.8)
![]() ; (15.9)
; (15.9)
Uzdevumā
![]() ,
,
![]() .
.
Salīdzināšanai
aprēķināsim iedzīvotāju vecuma standartnovirzi un vērtējuma intervālus,
izmantojot parametriskās metodes un ignorējot to, ka iedzīvotāju sadalījums pēc
vecuma atšķiras no normālā sadalījuma.
Izmantojot
iedzīvotāju grupējumu pēc vecuma vienu gadu lielos intervālos vecumā no 0 līdz
64 gadiem un piecu gadu lielos intervālos lielākiem vecumiem, ieguvām
standartnovirzi 22,42 gadi.
Kvartiļu vidējā
novirze 18,5 ir ievērojami mazāka nekā parastā standartnovirze 22,4, jo
atspoguļo pazīmes variāciju tikai variācijas apgabala centrālajā daļā (50%
novērojumu), bet parastā standartnovirze - visā variācijas apgabalā.
Spriežot līdzīgi
varētu sagaidīt, ka arī deciļu vidējā novirze būs mazāka (šoreiz nedaudz) par parasto standartnovirzi,
jo aptver tikai 80% novērojumu. Uzdevuma
atrisinājums parāda pretējo: deciļu vidējā novirze 30,3 ir ievērojami
lielāka nekā parastā standartnovirze - 22,4.
Izskaidrojums ir
jāmeklē tajā apstāklī, ka uzdevumā izmantotais sadalījums krasi atšķiras no
normālā ar daudz lielāku vienību koncentrāciju sadalījuma kreisajā zarā 2.
Tas nozīmē, ka vidēji lielu noviržu no vidējā empiriskajā sadalījumā ir daudz
vairāk nekā normālajā. Tieši šīs vidēji lielās novirzes palielina deciļu vidējo
novirzi.
Salīdzināšanai varam
apŗēķināt arī vērtējuma intervālus pēc normālā sadalījuma likuma, kuri atbilst
kvartiļu un deciļu intervāliem.
Normālā sadalījuma
varbūtību koeficienti, kas atbilst varbūtībām 0,5 un 0,8, ir 0,67 un 1,28. Līdz
ar to robežkļūdas
![]() (15.10)
(15.10)
ir ![]()
un ![]() .
.
Izmantojot vidējo
vecumu ![]() gadi, varam izveidot
atbilstošos vērtējuma intervālus
gadi, varam izveidot
atbilstošos vērtējuma intervālus
![]() . (15.11)
. (15.11)
Ar varbūtību 0,5 saistītais
intervals iznāk
![]() (gadi),
(gadi),
bet ar varbūtību 0,8
![]() (gadi).
(gadi).
Atšķirības ir
jāizskaidro līdzīgi kā to darijām, salīdzinot parasto standartnovirzi ar
kvartiļu un deciļu vidējām novirzēm.
Neparametriskos
relatīvās variācijas rādītājus var veidot līdzīgi variācijas koeficientam,
tikai parastās standartnovirzes vietā jāņēm kvartiļu vai deciļu vidējā novirze,
bet aritmētiskā vidējā vietā - mediāna. Šos rādītājus var izteikt procentos.
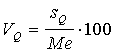 ; (15.12)
; (15.12)
![]() . (15.13)
. (15.13)
_________________
2 Empīriskā sadalījuma asimetrijas
koeficients ir 0,23, normālā sadalījumā jābūt 0,
bet ekscesa
koeficients 2,08, normālā sadalījuma jābūt 3,0.
Uzdevumā
![]() ,
,
![]() .
.
Deciļu variācijas
koeficients vienmēr būs lielāks nekā kvartiļu variācijas koeficients, jo deciļu
variācijas koeficients atspoguļo dažādību 80% novērojumu masā, kamēr kvartiļu
variācijas koeficients - tikai 50% pamatmasā.
Salīdzinājumam
izrēķināsim parasto variacijas koeficientu izmantojamiem 15.1. tabulas datiem
![]() .
.
Šis koefiecients pēc
skaitliskās vērtības atrodas vidū starp kvartiļu un deciļu variācijas
koeficientiem to pašu iemeslu dēļ, kuri bija uzrādīti, apspriežot vidējās un
standartnovirzes, jo variācijas koefiecienti ir tieši atkarīgi no šim novirzēm.
Jāatzīmē, ka visi
variācijas koeficienti ir daudz lielāki par 33 %, kas ir augšējā robeža lai
empīrisko sadalījumu varētu vērtēt kā tuvu normālam sadalījumam.
Nobeigumā jāsecina,
ka ir iespējami vairāki, skaitliski atšķirīgi neparametriskie variācijas rādītāji. Bez tiem, kurus
ieguvām pretstatot trešo un pirmo kvartili un devīto un pirmo decili, varam izveidot vēl citus.
Piemēram, pretstatot astoto decili otrai. Pēdējā gadījumā raksturosim variāciju
60% novērojumu galvenajā masīvā. Līdzīgus rādītājus var izveidot, izmantojot
kvintiles, centiles u.c. struktūras rādītājus.
Zināma nenoteiktība
ir jāvērtē kā šo rādītāju trūkums. Izvēle starp tiem ir jāizdara atbilstoši
uzdevuma profesionālai nostādnei: kāda pētāmās kopas daļa dod atbildi uz
izvirzītajiem jautājumiem. Ja tā ir kopas centrālā daļa, var lietot kvartiļu rādītājus, ja t.s. galvenais masīvs
- deciļu (atstājot ārpusē 20% novērojumu). Ja grib izmantot visus novērojuma
datus, atsijājot tikai krasi atšķīrīgos artefaktus dažu procentu robežās,
jāizmanto centiles un uz tiem balstīti rādītāji. Lietojot datortehniku,
aprēķināt centiles var samērā viegli. Turklāt nav jāizdrukā visas centiles, bet
vairumā gadījumu pietiek izdrukāt tikai dažas vienā vai abos sadalījuma zaros.
15.2. Hī kvadrāta kritērijs
neparametriskā statistikā
Kā jau bija minēts,
par neparametriskām statistikas metodēm
šaurā nozīmē sauc dažādas metodes un kritērijus statistisko hipotēžu pārbaudei;
vērtējumu intervālu aprēķināšanai, statistisko lēmumu pieņemšanai. Visu šādu
uzdevumu risināšana prasa izmantot varbūtību teoriju.
Hī kvadrāta
kritēriju izmanto statistisko hipotēžu pārbaudei dažāda rakstura uzdevumos.
Lietojot Hī kvadrāta
kritēriju, savā starpā nesalīdzina kādus divu izlašu parametrus (aritmētiskos
vidējos, standartnovirzes u.c.), ne arī neparametriskos rādītājus (modas,
kvartiles v.c.), bet pašus šo izlašu empīriskos sadalījumus pēc interesējošās
pazīmes.
Lai salīdzinātu divu
izlašu empīriskos sadalījumus, var izmantot grupējumus tiklab pēc kvantitatīvām
kā atributivām pazīmēm. Vienīgi grupu skaitam un intervāliem abu sadalījumu
grupējumos ir jābūt vienādiem. Vēl jāseko, lai vienību skaits visās grupās būtu
pietiekami liels, katrā ziņā ne mazāks par 5.
No pēdējā priekšnoteikuma seko, ka absolūto biežumu vietā nevar izmantot
relatīvos.
Bieži Hī kvadrātu
lieto, lai pārbaudītu empīriskā sadalījuma atbilstību kādam teoretiskam
sadalījumam (vienmērīgam, normālam, logaritmiski normālam u.c.). Teorētisko
sadalījumu izvēlas un aprēķina atbilstoši izvirzītai hipotēzei. Pēdējās grupas
uzdevumu atrisināšana arī tehniski vienkāršāka.
Tā kā pēdējā
gadījumā viens no salīdzināmajiem sadalījumiem ir teorētisks un arī pirmajā
gadījumā lēmumu par hipotēzi pieņem, izmantojot Hī kvadrāta teorētisko
sadalījumu, daži autori Hī kvadrāta kritēriju un attiecīgos uzdevumus nepieskaita neparametriskiem. Citi autori,
turpretīm, tos neparametriskiem pieskaita. Jāatzīst, ka arī citos gadījumos
parametrisko un neparametrisko metožu lietošana nav stingri norobežojama,
piemēram, izdarot aprēķinus, kas balstās uz varbūtību binomiālo sadalījumu.
15.2.1. Sadalījuma vienmērīguma
novērtēšana
15.2.1.
Uzdevums. Latvijas iedzīvotāju dzīves apstākļu pētījuma ietvaros 1994.g. septembra
aptaujā respondentiem jautāja, kam
pieder mājoklis, kurā ģimene (mājasaimniecība) dzīvo. Latviešu un citu tautību
ģimenes deva pēc apkopošanas vizuāli atšķirīgas atbildes (15.3. tabula).
15.3. tabula
Latviešu
un citu tautību mājsaimniecību sadalījums pēc īpašnieka,
kam pieder aizņemtais mājoklis
|
|
Mājokļa īpašnieks |
|
|
|
Tautībtips |
valsts vai pašvaldība |
ģimene, tās
loceklis, cita privātpersona |
Kopā |
|
Latvieši |
671 |
723 |
1394 |
|
Citu tautību |
807 |
207 |
1014 |
|
Kopā |
1478 |
930 |
2408 |
Datu avots: LR Valsts
Statistikas komitejas 1994.g. septembra iedzīvotāju dzīves apstākļu aptauja.
Tautību ziņā jauktas mājsaimniecības šajā
tabulā nav atspoguļotas.
Ja vairāk nekā 50%
latviešu ģimeņu dzīvoja savā, savas ģimenes loceklim vai svešam
privātīpašniekam piederošā mājoklī, tad 80% citu tautību (g.k. krievu) ģimenes
- valstij vai pašvaldībai piederošā mājoklī. Pirms no šiem faktiem izdarīt
vēsturiskus un sociālus secinājums, ir jāpārbauda minēto atšķirību statistiskā
nozīmība, jo dati neatspoguļo visas Latvijas ģimenes, bet tikai 2408 ģimeņu
lielu izlasi.
Izvirzām nulles
hipotēzi, ka latviešu un citu tautību ģimenes pēc aizņemtā mājokļa piederības
ģenerālkopā neatšķiras un vērojamās atšķirības izlasē var izskaidrot ar
nejaušību.
Uzdevumā dotais
izlases ģimeņu grupējums četrās elementārgrupās un četrās marginālās
(starpsummu) grupās ir empīriskais sadalījums.
Lai pilnībā
formulētu pārbaudāmo hipotēzi, ir jāaprēķina teorētiskais sadalījums, kas
atbilst hipotēzei, ka mājokļa īpašumtiesiskā piederība statistiski nav saistīta
šī mājokļa iedzīvotāju tautību. Tas ir vienmērīgs sadalījums, kurā, salīdzinot
ar empīrisko, tiek saglabāts kopējais ģimeņu skaits (2408) un tā sadalījums
marginālās grupās.
Teorētiskais ģimeņu
skaits elementārgrupās ir jāaprēķina, sadalot marginālās summas (1394 un
1014) proporcionāli visu tautību ģimeņu
sadalījumam dažādos īpašumtiesiskās piederības mājokļos, t.i. proporcionāli
summām 1478 un 930, resp. 0,6138 un 0,3862 viena daļās.
Iegūstam 15.4. tabulu, kurā biežumi visās rindiņās ir
proporcionāli.
Tagad pārbaudamo
hipotēzi var formulēt šādi. 15.3. un 15.4. tabulās uzrādītie sadalījumi
neatšķiras būtiski; var uzskatīt, ka tie ir divas dažādas izlases no vienas
ģenerālkopas.
15.4. tabula
15.3.
tabulai atbilstošs vienmērīgs sadalījums, saskaņā ar hipotēzi, ka visu tautību
izvietojums dažādiem īpašniekiem piederošos mājokļos ir nejaušs.
|
|
Mājokļa īpašnieks |
|
|
|
Tautībtips |
valsts vai pašvaldība |
ģimene, tās
loceklis, vai cita privātpersona |
Kopā |
|
Latvieši |
856 |
538 |
1394 |
|
Citu tautību |
622 |
392 |
1014 |
|
Kopā |
1478 |
930 |
2408 |
Lai izvirzīto hipotēzi pārbaudītu ar Hī kvadrāta
kritēriju, ir jāizdara sekojošais.
1.
Izmantojot empīriskā un teorētiskā sadalījuma biežumus, jāaprēķina empīriskā Hī
kvadrāta lielums, izmantojot formulu
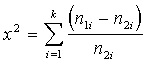 , (15.14)
, (15.14)
kur ![]() - empīriskā sadalījuma
biežumi i grupās;
- empīriskā sadalījuma
biežumi i grupās;
![]() - teorētiskā
sadalījuma biežumi atbilstošās grupās;
- teorētiskā
sadalījuma biežumi atbilstošās grupās;
k -
grupu skaits.
Jāievēro, ka par ![]() jāņem empīriskā, bet
par
jāņem empīriskā, bet
par ![]() - teorētiskā
sadalījuma biežumi; pēdējie jāizmanto
daļskaitļu saucējos.
- teorētiskā
sadalījuma biežumi; pēdējie jāizmanto
daļskaitļu saucējos.
Tā kā uzdevumā ir
tikai četras grupas, aprēķinus var izdarīt, tieši ievietojot formulā vajadzīgos
skaitļus. Ja grupu būtu vairāk, būtu lietderīgi aprēķinus sakārtot darba tabulā
vai sastādīt programmu skaitļotājam, izmantojot atmiņas.
![]()
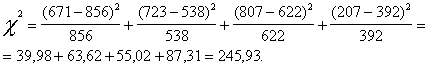
2. Lai Hī kvadrāta
kritisko vērtību tabulā nolasītu vajadzīgo robežvērtību, ir jāizvēlās
(jāpamato) nulles hipotēzes pārbaudes varbūtība, resp., nozīmības līmenis.
Vairumā mācību grāmatu ir publicētas tabulas hipotēzes pārbaudei ar varbūtību
0,95 (nozīmības līmenis 0,05) un 0,99 (0,01). Ekonomikas pētījumos parasti
pietiek ar mazāko varbūtību, tādēļ izvēlamies to. Vēl ir jānosaka brīvības
pakāpju skaits. Šajā gadījumā to aprēķina no elementārgrupu skaita 4 atskaitot
neatkarīgo lineāro saistību skaitu, kas saista tabulas datus. Tādas ir 3:
kopējā summa un rindu (vai aiļu) summas. Vēl var saskatīt arī citas saistības,
bet tās izriet no iepriekšējām. Līdz ar to grupējumā ir tikai viena brīvības
pakāpe. Par pēdējo apgalvojumu var pārliecināties vēl citādi. Izgatavojiet
tabulas maketu atbilstoši 15.3. tabulai un ierakstiet tajā rindu, aiļu un kopējo summu. Vienā no tukšajām centrālajām
rūtiņām variet ierakstīt jebkuru skaitli (ja citās negribat rakstīt negatīvus
skaitļus, tad gan nevar rakstīt lielāku
par kopsummu -2408). Tūliņ viegli pārliecināties, ka pārējās trīs rūtiņās,
lai saglabātu summu pareizību, ir
jāraksta pilnīgi noteikti skaitļi. Iespēja vienā rūtiņā ņemt jebkuru skaitli ir
tā viena brīvības pakāpe.
3. Tālāk
matemātiskajās tabulās ir jāatrod Hī kvadrāta robežvērtība, kas atbilst
varbūtībai 0,95 ![]() un viena brīvības
pakāpei
un viena brīvības
pakāpei ![]() . Fragments no vajadzīgām tabulām ir parādīts 15.5. tabulā.
. Fragments no vajadzīgām tabulām ir parādīts 15.5. tabulā.
15.5. tabula
Fragments
Hī kvadrāta kritiskajām robežām hipotēzes pārbaudei
ar
varbūtību 0,95 (a = 0,05)
|
Brīvības pakāpju skaits |
1
2 3 4 5 6
7 8 10 |
|
Kritiskā robeža |
3,84 5,99 7,81
9,49 11,1 12,6
14,1 15,5 18,3 |
Redzam ka ![]() .
.
4. Empiriskais ![]() jāsalīdzina ar
jāsalīdzina ar ![]() kritisko robežu
kritisko robežu ![]() un jāpieņem lēmums.
245,93 > 3,84, resp.,
un jāpieņem lēmums.
245,93 > 3,84, resp., ![]() , un nulles hipotēzi var noraidīt ar prasīto varbūtību. Tā kā
salīdzināmie lielumi atšķiras vairākkārt, nulles hipotēzi var noraidīt ar daudz
lielāku varbūtību nekā izvēlētā 0,95 jeb kā saka ''ar lielu pārsvaru''.
, un nulles hipotēzi var noraidīt ar prasīto varbūtību. Tā kā
salīdzināmie lielumi atšķiras vairākkārt, nulles hipotēzi var noraidīt ar daudz
lielāku varbūtību nekā izvēlētā 0,95 jeb kā saka ''ar lielu pārsvaru''.
Izlases aptauja ir
pierādījusi ka latvieši statistiski nozīmīgi
vairāk dzīvo pašiem vai citiem privātīpašniekiem piederošos mājokļos,
bet citu tautību ģimenes ir būtiski vairāk saņēmušas dzīvokļus valsts un
pašvaldību namos.
Kādi vēsturiski un
sociāli apstākļi ir izraisījuši šīs atšķirības, tas jau ir profesionālas
sociāli ekonomiskas analīzes uzdevums.
Empīrisko Hī
kvadrātu 2 x 2 sadalījuma tabulai var aprēķināt arī tieši, neizveidojot
hipotētisko vienmērīgo sadalījumu (15.4. tabulu). Tas atvieglo izskaitļošanu,
bet starprezultāti ir mazāk uzskatāmi.
Jālieto formula
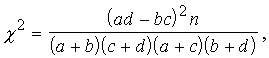 (15.15)
(15.15)
kur a ... d -
absolūtie biežumi 2 x 2 tabulā pēc šādas shēmas
|
a |
b |
a+b |
|
c |
d |
c+d |
|
a+c |
b+d |
n |
n - novērojumu skaits.
Iepriekšējā uzdevumā, ievietojot formulā 15.3. tabulas
datus, iegūstam
![]() .
.
Rezultāts, kas
iegūts, lietojot pamatformulu, atšķiras vienīgi starprezultātu noapaļošanas
rezultātā.
Ievietojot 15.15.
formulā vienmērīga sadalījuma datus (15.4. tabula), ir jāiegūst Hī kvadrāts,
kas no nulles drīkst atšķirties vienīgi noapaļošanas kļūdu rezultātā.
![]()
15.2.2. Divu izlašu sadalījumu
savstarpēja salīdzināšana
Nereti rodas
vajadzība pārbaudīt, vai divas izlases pēc to sadalījumiem var vērtēt kā
ņemtas no vienas un tās pašas ģenerālkopas, vai tās
pārstāv divas atšķirīgas ģenerālkopas. Šādi
uzdevumi bieži rodas biometrijā, kad
nepieciešams savā starpā
salīdzināt kādas divas augu, dzīvnieku v.c. paraugkopas. Hipotēze par to, kāds
ir abu salīdzināmo izlašu sadalījums, nav jāizvirza. Ir vajadzīgs vienīgi, lai
abu izlašu vienības būtu sagrupētas grupās, izmantojot vienus un tos pašus
intervālus. Tehniski darbs ir nedaudz sarežģitāks, nekā salīdzinot empīrisko sadalījumu ar teorētisko (skat.
iepriekšējo paragrāfu).
Var izšķirt divus
gadījumus: 1) abu salīdzināmo izlašu lielums (vienību skaits tajās) ir vienāds
un 2) abu salīdzināmo izlašu lielums ir
dažāds.
1. Ja abu
salīdzināmo izlašu lielums ir vienāds empīrisko Hī kvadrātu aprēķina pēc
formulas ³
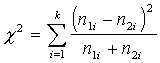 , (15.16)
, (15.16)
kur:
![]() - pirmās izlases
vienību skaits i grupā,
- pirmās izlases
vienību skaits i grupā,
![]() - otrās izlases
vienību skaits i grupā,
- otrās izlases
vienību skaits i grupā,
k -
grupu skaits.
Brīvības pakāpju
skaitu nosaka kā ![]() , jo abas izdalītās izlases saista viens nosacījums -
grupu kopskaits. Hī kvadrāta kritisko vērtību tāpat kā iepriekš nolasa
matemātiskajās tabulās, salīdzina empīrisko Hī kvadrātu ar tā kritisko
robežvērtību un pieņem lēmumu.
, jo abas izdalītās izlases saista viens nosacījums -
grupu kopskaits. Hī kvadrāta kritisko vērtību tāpat kā iepriekš nolasa
matemātiskajās tabulās, salīdzina empīrisko Hī kvadrātu ar tā kritisko
robežvērtību un pieņem lēmumu.
Praksē tomēr biežāk
ir jāsalīdzina divu dažāda lieluma izlašu sadalījumi, tādēļ piemēru dosim šim
gadījumam.
2. Ja abu
salīdzināmo izlašu vienību skaits nav vienāds, tad iepriekš minētajā empīriskā
Hī kvadrāta formulā ir jāiestrādā statistiskie svari, par tiem ņemot abu izlašu
kopējo vienību skaitu
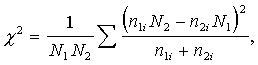 (15.17)
(15.17)
___________________
3 Formulas pamatojums ir pievienots
paragrāfa beigās.
kur ![]() un
un ![]() - pirmās un otrās
izlases vienību kopskaits 4:
- pirmās un otrās
izlases vienību kopskaits 4:
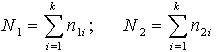 .
.
15.2.2. Uzdevums. Ir izdarīti koku augstuma x mērījumi divās ar dažādām metodēm ierīkotās priežu kultūru
audzēs, iegūstot šādus datus (15.6. tabula). Pārbaudīt vai abas audzes pārstāv
vienu un to pašu ģenerālkopu, vai tās ir ņemtas dažādām ģenerālkopām.
15.6. tabula
Empīriskā
Hī kvadrāta aprēķins divu izlašu salīdzināšanai 5
|
Priežu |
Koku skaits |
Aprēķinātie
lielumi |
||||||
|
augstums metri
|
1.audzē
|
2.audzē
|
|
|
|
|
|
|
|
|
|
|
1000 |
500 |
500 |
250000 |
10 |
25000 |
|
3,90 |
6 |
18 |
1200 |
1800 |
-600 |
360000 |
24 |
15000 |
|
4,00 |
10 |
37 |
2000 |
3700 |
-1700 |
2890000 |
47 |
61489 |
|
4,10 |
23 |
83 |
4600 |
8300 |
-3700 |
13690000 |
106 |
129151 |
|
4,20 |
28 |
42 |
5600 |
4200 |
1400 |
1960000 |
70 |
28000 |
|
4,30 |
19 |
8 |
3800 |
800 |
3000 |
9000000 |
27 |
333333 |
|
|
|
|
1800 |
700 |
1100 |
1210000 |
16 |
75625 |
|
Kopā |
100 |
200 |
20000 |
2000 |
0 |
X |
300 |
667598 |
Tā kā rēķinot Hī
kvadrātu, nevienā grupā nedrīkst būt mazāk kā pieci novērojumi, turklāt abos
sadalījumos grupām (intervāliem) jābūt vienādiem, abos sadalījumos pirmās trīs
un pēdējās trīs grupas ir jāapvieno.
![]() .
.
_________________
4 Ar N tradicionāli apzīmē vienību
skaitu ģenerālkopā. Šeit un arī turpmāk izņēmuma kārtā ar to apzīmējam vienību
skaitu izlasē, lai izvairītos no sarežģītas n indeksācijas, piemēram, ar augšējiem indeksiem.
5 Datu avots: Liepa I. Biometrija. R.:
1974. - 92.lpp. (aprēķini precizēti).
Brīvības pakāpju
skaitu, kas nepieciešams Hī kvadrāta kritiskās vērtības nolasīšanai, divu
izlašu salīdzināšanas gadījumā, aprēķina no grupu skaita (cik palikušas pēc
apvienošanas) atskaitot vienu ![]() , jo pastāv tikai viens saistošs nosacījums - abu izlašu
kopīgais grupu skaits. Tātad mūsu uzdevumā
, jo pastāv tikai viens saistošs nosacījums - abu izlašu
kopīgais grupu skaits. Tātad mūsu uzdevumā ![]() .
.
Saglabājot
iepriekšejā uzdevumā izmantoto hipotēzes pārbaudes varbūtību ![]() , kritisko Hī kvadrāta vērtību var nolasīt 15.5. tabulā
, kritisko Hī kvadrāta vērtību var nolasīt 15.5. tabulā
![]()
Tā kā 33,38>12,6,
resp., ![]() , nulles hipotēze, kas apgalvo, ka abas izlases ņemtas no
vienas ģenerālkopas, ir jānoraida. Katra izlase pārstāv citu ģenerālkopu,
priežu audzes pēc koku garuma atšķiras statistiski nozīmīgi.
, nulles hipotēze, kas apgalvo, ka abas izlases ņemtas no
vienas ģenerālkopas, ir jānoraida. Katra izlase pārstāv citu ģenerālkopu,
priežu audzes pēc koku garuma atšķiras statistiski nozīmīgi.
Empīriskā Hī
kvadrāta aprēķināšanas speciālo formulu (15.16), salīdzinot ar pamatformulu
(15.4.) pamato šādi.
Kā nezināmā
teorētiskā sadalījuma biežumu ![]() pirmo tuvinājumu
pieņem abu empirisko sadalījumu atbilstošo intervālu biežumu vidējos katrā i
grupā (indeksi i turpmāk, kur tas nerada pārpratumus,
izlaisti).
pirmo tuvinājumu
pieņem abu empirisko sadalījumu atbilstošo intervālu biežumu vidējos katrā i
grupā (indeksi i turpmāk, kur tas nerada pārpratumus,
izlaisti).
![]() ; (15.18)
; (15.18)
Ievietojot šos lielumus Hī kvadrāta pamatformulā (15.14.)
iegūstam 2k saskaitāmos
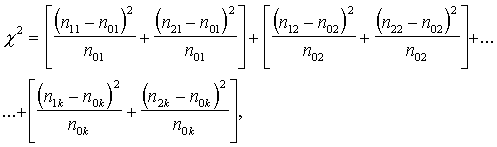
kur pirmais indekss - izlases numurs ( 0 - vidējais
biežums), otrais indekss - grupas numurs.
Ņemot vērā, ka
![]() , (15.19)
, (15.19)
katru kvadrātiekavu
saturu var pārveidot: ievietojot no vietā tā
vērtību no (15.19.), izdarot kāpināšanas darbības un izteiksmi vienkāršojot:
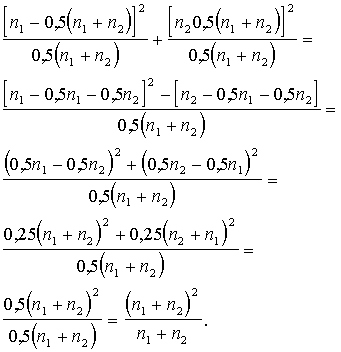
Tā kā Hī kvadrāta formulā ir k
šādi saskaitāmie (atbilstoši grupu skaitam), tad
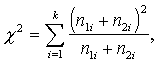
kas atbilst formulai (15.16.).
15.3. Hī kvadrāta
alternatīvi kritēriji
15.3.1. Vulfa G - kritērijs
Vulfa G - kritēriju lieto, lai pārbaudītu
hipotēzi par to, ka sadalījums četrās elementārgrupās (četru rūtiņu sadalījums)
ir vienmērīgs. Tatad šis kritērijs ir derīgs kā alternatīva 15.2.1. paragrāfā
parādīta un tam analogu uzdevumu risināšanai.
Empīrisko G lielumu aprēķina pēc īpašas formulas,
bet teorētisko robežvērtību atrod Hī kvadrāta kritisko vērtību tabulās.
Empīrisko G lielumu aprēķina ar šādu formulu
![]() , (15.20)
, (15.20)
kur
![]()
kur savukārt n -
absolūtie biežumi četrās elementārgrupās (četri saskaitāmie);
![]()
kur N - visu
novērojumu skaits;
![]()
kur ![]() - novērojumu skaits
marginālās (starpsummu) grupās (četri saskaitāmie).
- novērojumu skaits
marginālās (starpsummu) grupās (četri saskaitāmie).
Izmantojot 15.2.1. paragrāfa piemēru (15.3. tabula),
visus vajadzīgos lielumus ![]() aprēķināšanai var
sakārtot 15.7. tabulā:
aprēķināšanai var
sakārtot 15.7. tabulā:
15.7.
tabula
|
8734,77 |
9519,61 |
20184,93 |
|
10803,02 |
2207,75 |
14037,12 |
|
21574,20 |
12713,44 |
37500,03 |

Ievērojam, ka G lielums
ir diezgan līdzīgs empiriskajam ![]() , ko aprēķinajām
, ko aprēķinajām
15.2.1. paragrāfā 245,93.
Teorētisko ![]() robežvērtību nolasa
tāpat kā 1.1. paragrāfā:
robežvērtību nolasa
tāpat kā 1.1. paragrāfā: ![]() .
.
Tā kā ![]() hipotēzi par
sadalījuma vienmērīgumu noraida ar varbūtību, lielāku par 0,95.
hipotēzi par
sadalījuma vienmērīgumu noraida ar varbūtību, lielāku par 0,95.
Ir norādes, ka
empīriskais G - rādītājs ir pat
teorētiski pamatotāks nekā parastais ![]() rādītājs.
rādītājs.
Ja vienību skaits
elementārgrupās nav liels un lēmumu par hipotēzi nevar pieņemt ar lielu
pārsvaru, ir lietderīgi izmantot elementārgrupu biežumu korekciju, kā to
ieteicis Jeits.
Korekciju izdara tā,
ka tos biežumus, kuri ir mazāki nekā sagaidāms, ja hipotēze par sadalījuma
vienmērību būtu pareiza, palielina par 0,5, bet kuri lielāki - samazina par
0,5. Uzdevumā ![]() būtu jaizskaitļo no
lielumiem (jāsalīdzina ar 15.3. tabulu):
būtu jaizskaitļo no
lielumiem (jāsalīdzina ar 15.3. tabulu):
|
671,5 |
722,5 |
|
806,5
|
207,5, |
Iegūstam ![]()
![]() nemainās.
nemainās. ![]() .
.
Koriģētais ![]() vienmēr ir nedaudz
mazāks nekā nekoriģētais G un tuvāks
empīriskajam
vienmēr ir nedaudz
mazāks nekā nekoriģētais G un tuvāks
empīriskajam ![]() .
.
15.3.2. Kolmagorova-Smirnova ![]() kritērijs
kritērijs
Kā alternatīvu Hī kvadrāta kritērijam, pārbaudot hipotēzi par
divu empīrisko sadalījumu atšķirības statistisko nozīmību, var izmantot
Kolmagorova-Smirnova ![]() kritēriju.
kritēriju.
Empīrisko ![]() lielumu aprēķina,
balstoties uz salīdzināmo empīrisko sadalījumu uzkrāto relatīvo biežumu
starpībām, lietojot formulu
lielumu aprēķina,
balstoties uz salīdzināmo empīrisko sadalījumu uzkrāto relatīvo biežumu
starpībām, lietojot formulu
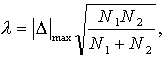 (15.21)
(15.21)
kur ![]() - divu uzkrāto
relatīvo biežumu lielākā starpība;
- divu uzkrāto
relatīvo biežumu lielākā starpība;
![]() un
un ![]() - novērojumu skaits
abās izlasēs.
- novērojumu skaits
abās izlasēs.
Metodi var lietot gan savstarpēji neatkarīgu, gan
atkarīgu izlašu salīdzināšanai. Nav jānodrošina, lai absolūtie biežumi visās
grupās būtu pietiekami lieli.
Kā piemēru vēlreiz izmantosim 15.6. tabulā dotos datus,
aprēķinus sakārtojot 16.8. tabulā.
15.8. tabula
Empīriskā
Kolmagorova-Smirnova ![]() aprēķins divu izlašu
salīdzināšanai
aprēķins divu izlašu
salīdzināšanai
|
|
|
|
|
|
|
|
|
|
3,60 |
1 |
0 |
0,01 |
0 |
0,01 |
0,000 |
0,010 |
|
3,70 |
1 |
1 |
0,01 |
0,005 |
0,02 |
0,005 |
0,015 |
|
3,80 |
3 |
4 |
0,03 |
0,020 |
0,05 |
0,025 |
0,025 |
|
3,90 |
6 |
18 |
0,06 |
0,090 |
0,11 |
0,115 |
0,005 |
|
4,00 |
10 |
37 |
0,11 |
0,185 |
0,21 |
0,300 |
0,090 |
|
4,10 |
23 |
83 |
0,23 |
0,415 |
0,44 |
0,715 |
0,275 |
|
4,20 |
28 |
42 |
0,28 |
0,210 |
0,72 |
0,925 |
0,205 |
|
4,30 |
19 |
8 |
0,19 |
0,040 |
0,91 |
0,965 |
0,055 |
|
4,40 |
7 |
4 |
0,07 |
0,020 |
0,98 |
0,985 |
0,005 |
|
4,50 |
1 |
2 |
0,01 |
0,010 |
0,99 |
0,995 |
0,005 |
|
4,60 |
1 |
1 |
0,01 |
0,005 |
1,00 |
1,000 |
0,000 |
|
Kopā |
100=
|
200=
|
1 |
1 |
x |
x |
|
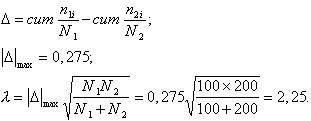
![]() kritisko vērtību var
aprēķināt ar samērā vienkāršu formulu
kritisko vērtību var
aprēķināt ar samērā vienkāršu formulu
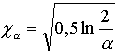 , (15.22)
, (15.22)
kur ![]() - izvēlētais
nozīmības līmenis. Tādēļ nav
nepieciešamas šo vērtību matemātiskās tabulas.
- izvēlētais
nozīmības līmenis. Tādēļ nav
nepieciešamas šo vērtību matemātiskās tabulas.
Izvēloties ![]() ,
,
![]()
Lēmumu, kā parasti,
pieņem, salīdzinot empīrisko ![]() vērtību ar kritisko
robežu. Uzdevumā
vērtību ar kritisko
robežu. Uzdevumā ![]() . Tas ļauj noraidīt nulles hipotēzi par to, ka abas izlases
ņemtas no vienas ģenerālkopas. Izlases pārstāv dažādas ģenerālkopas.
. Tas ļauj noraidīt nulles hipotēzi par to, ka abas izlases
ņemtas no vienas ģenerālkopas. Izlases pārstāv dažādas ģenerālkopas.
15.4. Atkārtotu novērojumu izvērtēšana
ar binomiālo sadalījumu
15.4.1. Trīskāršā testa rezultātu
novērtēšana
Nosakot standartus
preču šķirām pēc kvalitātes, kā arī kontrolējot kvalitātes radītāju izpildi, ir
ļoti svarīgi zināt cilvēka jūtīgumu pret nelielām kvalitātes izmaiņām, piem.,
cukura īpatsvaru ievārījumā, alkohola saturu alū, piena skābumu u.tt. Šajā nolūkā
bieži izmanto t.s. trīskāršo testu. Vienādi sagatavotai ekspertu grupai piedāvā
novērtēt trīs paraugus, no kuriem divi ir pilnīgi vienādi, bet trešais nedaudz
atšķiras - ar sākotnēji iecerēto pielaidi. Paraugu pasniegšanas secība ir
nejauša un ekspertiem nav zināma. Ja eksperts atšķirīgo paraugu ir atradis,
uzskata, ka gadījuma notikums ir noticis; ja eksperts norāda citu paraugu - nav
noticis. Tā kā darbojas vairāki eksperti, rezultāti jāvērtē kā atkārtoti
izmēģinājumi.
Daļa ekspertu
norādīs īstenībā atšķirīgos paraugus arī tad, ja patiesībā viņus neatšķirs. Ja
ievērojama daļa ekspertu atšķirīgos paraugus spēj atšķirt, tad pareizo
norādījumu būs būtiski vairāk nekā to nodrošina nejaušība.
15.4.1. Uzdevums. Trīskāršo testu ir izpildījuši 8 eksperti, no viņiem 4
atšķirīgo paraugu ir norādījuši pareizi, bet 4 - nē. Novērtēt, vai šāds
rezultāts liecina, ka paraugu atšķirības cilvēki spēj sajust, vai iegūtais rezultāts varēja rasties arī
nejaušības dēļ.
Uzdevuma analīze un atrisinājums. Novērojumu
rezultātus šajā gadījumā fiksē kā alternatīvas atbildes: paraugs ir atšķirts, paraugs nav atšķirts.
Rezultātu var izteikt arī ar atbildēm ''ja'' un ''nē'', kodēt ar skaitļiem 1 un
0. Kādi skaitliski vai procentu samēri starp novērojumiem netiek prasīti un
netiek pielaisti. Piemēram, ekspertam
neprasa norādīt, ka paraugs ir ''ļoti'' atšķirīgs, vai ''tikko manāmi''
atšķirīgs, vēl jo mazāk - mēģināt noteikt kādas vielas daudzumu paraugos vai
citu kvantitatīvu rādītāju. Tātad ir savāktas alternatīvas atbildes par
atkārtotiem novērojumiem.
Izpildot trīskāršu
testu, ja visi paraugi īstenībā būtu vienādi, bet viens no viņiem iezīmēts ar
ekspertam nezināmu zīmi, iezīmētā parauga uzrādīšanas varbūtība būtu 1/3. Tā ir
rezultātu novērtēšanas apriorā bāze.
Izvērtējot
novērojumā faktiski iegūtos rezultātus, vispirms aprēķina atšķirīga parauga
uzrādīšanas relatīvo biežumu. Apzīmējot novērojumu (ekspertu) skaitu ar n, bet pareizo norādījumu skaitu ar m, iegūstam, ka relatīvais biežums v ir
![]() .
.
Tas ir lielāks par aprioro varbūtību, ja visi paraugi būtu vienādi.
Talāk ir jāpārbauda,
vai relatīvais biežums 0,5 būtiski atšķiras no varbūtības 1/3 = 0,333, vai šo
atšķirību var izskaidrot ar nejaušību.
Apzīmējam ar p relatīvā biežuma (v = 0,5) robežu, uz
kuru tas tiektos, ja trīskāršo testu izpildītu neierobežoti daudz ekspertu; ar ![]() - aprioro varbūtību
uzrādīt iezīmētu paraugu, ja visi paraugi ir vienādi (p = 1/3). Tad var
matemātiski formulēt nulles hipotēzi
- aprioro varbūtību
uzrādīt iezīmētu paraugu, ja visi paraugi ir vienādi (p = 1/3). Tad var
matemātiski formulēt nulles hipotēzi ![]() .
. ![]() jeb
jeb ![]() un saukt to par nulles
hipotēzi.
un saukt to par nulles
hipotēzi.
Saskaņā ar šo
hipotēzi, ja atšķirīgā parauga īpatnības ir zem cilvēka jūtīguma robežas,
atkārtojot triskāršo testu neierobežoti daudz reižu, abas varbūtības (p un ![]() ) būtu vienādas.
) būtu vienādas.
Uzdevuma
atrisinājums ir saistīts ar jautājumu, vai vienīgā izdarītā novērojumu sērija
atļauj noraidīt izvirzīto hipotēzi ar pietiekami augstu varbūtību.
Šajā nolūkā
atradīsim vismazāko pareizo atbildi noteikušo ekspretu skaitu ![]() , kurš jau atļauj noraidīt izvirzīto nulles hipotēzi ar
vajadzīgo varbūtību. Tad, ja vienīgajā izdarītajā novērojumu sērijā iznāks, ka
, kurš jau atļauj noraidīt izvirzīto nulles hipotēzi ar
vajadzīgo varbūtību. Tad, ja vienīgajā izdarītajā novērojumu sērijā iznāks, ka ![]() , hipotēzi noraidisim, bet ja
, hipotēzi noraidisim, bet ja ![]() , hipotēze paliks spēkā.
, hipotēze paliks spēkā.
Ir zināms, ka,
izdarot atkārtotus novērojumus, no kuriem gadījuma notikums katrā novērojuma
notiek ar varbūtību p, varbūtību, ka n novērojumos notikums notiks tieši m
reizes, var aprēķināt ar Bernulli formulu
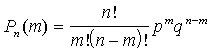 . (15.23.)
. (15.23.)
Ņemot m = 0; 1; 2; ... un aprēķinot to
varbūtības, iegūstam binomiālo sadalījumu
![]() .
.
Izvirzītajā uzdevumā
p = 1/3 ![]() 0,3333, n = 8, m = 0;
11; 2; ...; 8. Atbilstošo binomiālo sadalījumu var aprēķināt ar Bernulli
formulu vai izrakstīt no speciālām matemātiskām tabulām.
0,3333, n = 8, m = 0;
11; 2; ...; 8. Atbilstošo binomiālo sadalījumu var aprēķināt ar Bernulli
formulu vai izrakstīt no speciālām matemātiskām tabulām.
15.9. tabulas
pirmajā rindā ir parādīts ekspertu skaits m
(no n = 8), kuri potenciāli var
norādīt iezīmēto paraugu. Otrajā rindā - varbūtība, ka tieši tāds ekspertu
skaits to izdarīs. Kā redzams, vislielākās varbūtības ir, ka to izdarīs 2 vai 3
eksperti, kas aptuveni atbilst trešdaļai no visu ekspertu skaita (8).
15.9. tabulas
trešajā rindā ir parādītas uzkrātās varbūtības sadalījuma labajā zarā,
pakāpeniski summējot no labās puses.
Lasām kopā tabulas pirmo un trešo rindu.
Ja visi paraugi būtu
vienādi, tad, varbūtība, ka iezīmētos paraugus uzrādīs visi 8 eksperti, ir
praktiski nulle. Varbūtība, ka tos uzrādīs 7 vai vairāk eksperti, ir niecīga -
0,003; varbūtība, ka tos uzrādīs 6 vai vairāk eksperti, ir maza - 0,02. Ja tik daudz
ekspertu (vismaz 6) būtu uzrādījuši
pareizos paraugus reālajā ekperimentā, nulles hipotēzi varētu droši noraidīt, jo tāds rezultāts nav
izskaidrojams ar nejaušību, tātad paraugi ir pazīti.
15.9. tabula
Binomiālais
sadalījums6, ja n = 8, p = 0,333
|
m |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
0,039 |
0,156 |
0,273 |
0,273 |
0,171 |
0,068 |
0,017 |
0,003 |
0,000 |
|
saskaitot no labās puses |
1,000 |
0,961 |
0,805 |
0,532 |
0,259 |
0,088 |
0,020 |
0,003 |
0,000 |
|
saskaitot no kreisās puses |
0,039 |
0,195 |
0,468 |
0,741 |
0,911 |
0,979 |
0,996 |
0,999 |
1,000 |
Ja konkrētajā
eksperimentā atšķirīgos paraugus būtu uzrādījuši 5 vai vairāk eksperti, tad,
noraidot nulles hipotēzi, mēs riskētu kļūdīties, pieļaujot t.s. pirmā veida
kļūdu7, ar varbūtību 0,088. Citiem vārdiem, nulles hipotēzi varētu
noraidīt ar varbūtību 1 - 0,088 = 0,912. Parasti ekonomikas uzdevumos tas ir
samērā pietiekami.
Ja konkretajā
eksperimentā pareizo paraugu ir uzrādījuši 4 eksperti, tad, noraidot nulles
hipotēzi, riskējam kļūdīties jau ar varbūtību 0,259. Tā ir pietiekoši liela;
šādā gadījumā nulles hipotēzi nenoraida.
Līdz ar to esam
noteikuši ![]() . Nulles hipotēzi varētu noraidīt (ar varbūtību 0,912), ja
atšķirīgos paraugus būtu uzrādījuši vismaz 5 eksperti no 8. Tā kā uzdevumā to izdarija četri
eksperti (m = 4), tad
. Nulles hipotēzi varētu noraidīt (ar varbūtību 0,912), ja
atšķirīgos paraugus būtu uzrādījuši vismaz 5 eksperti no 8. Tā kā uzdevumā to izdarija četri
eksperti (m = 4), tad ![]() un nulles hipotēzi ar
pietiekoši augstu varbūtību noraidīt nevar. Precīzāk : to var noraidīt ar
varbūtību 1 - 0,259 = 0,741, ko parasti uzskata par nepietiekošu.
un nulles hipotēzi ar
pietiekoši augstu varbūtību noraidīt nevar. Precīzāk : to var noraidīt ar
varbūtību 1 - 0,259 = 0,741, ko parasti uzskata par nepietiekošu.
15.4.2. Grafiska ilustrācija
15.2. attēlā ir
parādīts binomiālā sadalījuma p = 0,333;
n = 8 varbūtību sadalījums, kas atbilst iepriekšējā uzdevuma nulles
hipotēzes saturam un 15.9. tabulas pirmo divu rindu skaitļiem.
Laukumu zem poligona
līnijas pieņemam par vienu vienību lielu, jo varbūtību summa (15.9. tabula 2.
rinda) ir viens.
Nulles hipotēzes
noraidīšanas kritiskais apgabals ir poligona labajā zarā. Ja izvirzīto nulles
hipotēzi gribam pārbaudīt ar varbūtību 0,95, resp., pieļaujam pirmā veida kļūdu
ar varbūtību 0,05, tad ir jāatrod tāds punkts uz skaitļu m ass, pret kuru vilktais perpendikuls nodala laukuma daļu labajā
zarā, kura lielums ir 0,05 no visa laukuma.
______________________
6 Tabulas otrā rinda ir mazs
izvilkums no plašākām tabulām, piem.
{jkktylth V. Deka. Ytgfhfvtnhbxtcrbt vtnjls
cnfnbcnbrb. c. 272. (visas tabulas 270.-274.lpp.)
vai Nf,kbws vfntvfnbxtcrjq
cnfnbcnbrb. V. DW FY CCCH 1968. - c. 346. - 347.
7
Pirmā veida kļūda ir kļūda, kuru pieļaujam noraidot īstenībā pareizu
nulles hipotēzi. Piemērā
atzīstot, ka
eksperti spēj paraugus izšķirt, ja īstenībā viņi to nespēj.

15.2. attēls.
Binomiālā sadalījuma p = 0,333; n = 8
varbūtību sadalījums (poligons)
Šāda uzdevuma
ilustrācija ir labi pazīstama no normālā sadalījuma netiešajiem uzdevumiem, bet
binomiālā sadalījuma gadījumā to tieši izmantot nevar. Laukuma daļas zem
sadalījuma līknes kā integrālās funkcijas var aprēķināt un tabulēt
nepārtrauktiem gadījuma lielumiem. Binomiālais sadalījums turpretī ir diskrētu
lielumu sadalījums. Tadēļ praktiskām vajadzībām ir jaizgatavo attēls, kurā uz
ordinātu ass ir atlikta uzkrāto varbūtību skala.
15.3. attēlā ar
1.poligonu ir parādīts uzkrāto varbūtību
sadalījums, summējot no labās puses.
Ar bultām ir parādīts, kā atrast nulles hipotēzes noraidīšanas jeb
kritisko apgabalu. Šajā nolūkā izvēlas hipotēzes pārbaudes nozīmības līmeni,
resp., varbūtību, ar kuru pieļauj pirmā veida kļūdu. Pieņemam ![]() . No šim skaitlim atbilstoša punkta uz ordinātu ass velkam
horizontālu taisni a līdz krustpunktam ar poligonu. No šī punkta velkam vertikālu
taisni b līdz krustpunktam ar abscisu
asi. Pēdējais punkts norāda robežu, aiz kuras pa labi atrodas nulles hipotēzes
noraidīšanas apgabals.
. No šim skaitlim atbilstoša punkta uz ordinātu ass velkam
horizontālu taisni a līdz krustpunktam ar poligonu. No šī punkta velkam vertikālu
taisni b līdz krustpunktam ar abscisu
asi. Pēdējais punkts norāda robežu, aiz kuras pa labi atrodas nulles hipotēzes
noraidīšanas apgabals.

15.3. attēls.
Binomiālā sadalījuma p = 0,333; n = 8
komulatīvo (uzkrāto)
varbūtību sadalījums,
summējot no labās puses (1.poligons)
un summējot no kreisās puses
(2.poligons).
Kritiskais punkts ir
![]() . Tā kā pēc uzdevuma satura
. Tā kā pēc uzdevuma satura ![]() var būt tikai vesels
skaitlis (ekspertu skaits, kas pareizi
uzrādījuši atšķirīgo paraugu), tad ir jaizvēlās tuvākais veselais
skaitlis, līdz ar to nedaudz paaugstinot
vai pazeminot nulles hipotēzes pārbaudes varbūtību.
var būt tikai vesels
skaitlis (ekspertu skaits, kas pareizi
uzrādījuši atšķirīgo paraugu), tad ir jaizvēlās tuvākais veselais
skaitlis, līdz ar to nedaudz paaugstinot
vai pazeminot nulles hipotēzes pārbaudes varbūtību.
Pieņemam, ka ![]() . Velkam no šī punkta vertikālu taisni līdz poligonam, tālāk
horizontālu taisni līdz ordinātu asij un nolasām jauno hipotēzes noraidīšanas
nozīmības līmeni
. Velkam no šī punkta vertikālu taisni līdz poligonam, tālāk
horizontālu taisni līdz ordinātu asij un nolasām jauno hipotēzes noraidīšanas
nozīmības līmeni![]() (precizais skaitlis 15.9. tabulas 3. rindā).
(precizais skaitlis 15.9. tabulas 3. rindā).
Tātad, ja izpildot
trīskāršo testu, no 8 ekspertiem 6 vai vairāk atšķirīgo paraugu ir norādījuši
pareizi, tad nulles hipotēzi, kas apgalvo, ka cilvēks šī parauga atšķirības
nespēj sajust, var noraidīt ar varbūtību 0,98, riskējot pieļaut pirmā veida
kļūdu ar varbūtību 0,02.
Citos gadījumos,
piemēram, tabulējot normālā sadalījuma integrālo funkciju, uzkrātos varbūtību
skaitļus atrod summējot (resp. atrodot noteikto integrāli) no kreisās puses
(2.poligons 15.3. attēlā). Mūsu piemērā
saprotamāku uzdevuma ilustrāciju iegūstam, summējot varbūtības no labās puses.
15.4.3. Dažas varbūtību binomiālā
sadalījuma īpašības
un sadalījuma robeža
Varbūtību binomiālā
sadalījuma raksturs (poligona veids grafiskajā attēlā) ir atkarīgs no
varbūtības p un novērojumu sērijas
lieluma n.
Ja varbūtība p daudz neatšķiras no 0,5 (līdz ar to
arī q ir tuvs 0,5), sadalījuma
poligons ir tuvs simetriskam. Ja vai nu p vai q ir mazs skaitlis, piemēram
0,1, sadalījuma poligons pie nelielām n
vērtībām ir krasi asimetrisks.
Ja novērojumu sērija
ir liela (n >50) sadalījuma
poligons kļūst tuvs simetriskam arī tad, ja p
vai q ir samērā mazs skaitlis, piem., p,g ![]() 0,1.
0,1.
Ja var pieņemt, ka
binomiālā sadalījuma poligons ir tuvs simetriskam, tad kā binomiālā sadalījuma
tuvinātu modeli var izmantot normālo
sadalījumu un statistiskās hipotēzes pārbaudīt ar klasiskām metodēm. Ja
tuvinājums ir nepietiekams, ir jāizdara aprēķini ar Bernulli formulu, kā
parādīts iepriekš, vai arī jāizmanto binomiālā sadalījuma matemātiskās tabulas.
Orientējoši var
pieņemt, ka tuvinājums ir
pietiekams, ja p,q >0,1 un n >50, bet, ja
p,q
>0,3, tad pietiek
n>30.
Ir gadījumi, ka
savāktie dati it tādi, kas neļauj pieņemt lēmumu par statistisko hipotēzi ar
pietiekamu pārsvaru, to noraidot vai paturot spēkā. Tieši šādos gadījumos ir
lietderīgi izmantot precīzas metodes. Ja dati ir tādi, ka hipotēzi var noraidīt
vai nenoraidīt ar lielu drošību, tad ir pilnīgi pietiekamas tuvinātas metodes.
Tādēļ dažreiz var sākt ar tuvinātām metodēm un tad, ja tās nedod atbildi ar
''lielu pārsvaru'', atkārtot aprēķinus jau ar precīzakām metodēm.
Dažos gadījumos, kad
lēmumu nevar pieņemt ar ''lielu pārsvaru'', kā arī tad, ja nav īsti pamatots
hipotēzes pārbaudes nozīmības līmenis, var pieņemt trešo lēmumu: novērojumu ir
jāturpina. Tāds galīgais lēmums varētu būt lietderīgs arī uzdevumā dotajā situācijā:
vēlams novērojumu atkārtot ar citiem ekspertiem un, ja iespējams, palielināt
ekspertu skaitu.
15.5. Hipotēzes par retiem notikumiem
tieša pārbaude
Vienkāršākajā
gadījumā ir dots četrlauciņu jeb 2 x 2 sadalījums un ir jāpārbauda, vai divas
izdalītās grupas pēc kādas pazīmes relatīvajiem biežumiem atšķiras statistiski
nozīmīgi. Turklāt relatīvie biežumi ir mazi.
Metodi raksturo 15.5.1. uzdevums.
Ir jāvērtē divi
piegādātāji pēc izbrāķēto partiju skaita, kuru abiem ir tik maz, ka izbrāķētās
partijas jāvērtē kā reti notikumi.
15.10. tabula
Piegādāto
partiju sadalījums derīgās un izbrāķētās
|
Piegādātāji |
Partiju skaits |
tajā skaitā |
|
|
|
|
izbrāķētas |
derīgas |
|
|
|
|
|
|
Pirmais |
50 |
1 |
49 |
|
Otrais |
70 |
2 |
68 |
|
|
|
|
|
|
K o p ā |
120 |
3 |
117 |
Analīze
un atrisinājums.
Izbrāķēto partiju
īpatsvars pirmajam piegādātājam ir 0,020, otrajam 0,0286, tātad pirmajam piegādātājam nedaudz mazāks. Bet šie
rādītāji ir iegūti, vadoties no retiem notikumiem - piegādāto partiju
izbrāķēšanas, Tādēļ rodas uzdevums pārbaudīt, vai pirmais piegādātājs, vadoties
no produkcijas kvalitātes viedokļa, ir uzticamāks nekā otrais.
No formālā viedokļa
šis uzdevums atgādina 15.2.1. uzdevumu, kuru risinājām nodaļā ''Hī kvadrāts''. Taču šoreiz Hī kvadrāta kritēriju izmantot nevar.
Lai strādātu ar Hī kvadrātu,
absolūtajiem biežumiem (novērojumu skaitam) katrā elementārgrupā (rūtiņā) ir
jābūt pietiekami lieliem, katrā ziņā
lielākiem par 5.
Tā kā izdalīto grupu
ir tikai divas (divi piegādātāji), to apvienošana, tādējādi palielinot
novērojumu skaitu grupās, nav iespējama. Tādēļ nulles hipotēzes pārbaudei
gadījumos, kur izšķiroša nozīme ir retiem notikumiem, ir jālieto kāda cita
metode.
Ja teorētiski
iespējamo biežumu sadalījumu četrlauciņu tabulā, kas nodrošina kopējo un
marģinālās (kopsummas rindas un ailes) summas, nav daudz, tad katra šāda
iespējamā sadalījuma varbūtību var aprēķināt tieši, izmantojot kombinatorikas
formulas8.
Ja no divām
ģenerālkopām (divu piegādātāju partijām) ir ņemtas izlases un konstatēts
notikuma iestāšanās skaits (izbrāķēto partiju skaits), tad iegūstam 2 x 2
rūtiņu sadalījumu
|
|
|
|
|
|
|
|
|
|
|
|
Ja ir fiksētas
summas ![]() tad vienu no
biežumiem, piemēram
tad vienu no
biežumiem, piemēram ![]() , var izvēlēties brīvi, bet tiklīdz šī izvēle ir izdarīta,
pārējie biežumi
, var izvēlēties brīvi, bet tiklīdz šī izvēle ir izdarīta,
pārējie biežumi ![]() kļūst fiksēti skaitļi, kuri var vienīgi nodrošināt vajadzīgās summas.
kļūst fiksēti skaitļi, kuri var vienīgi nodrošināt vajadzīgās summas.
Tādēļ, izrēķinot
piemēram ![]() varbūtību, tā
vienlaikus raksturo arī viena konkrēta 2 x 2 sadalījuma varbūtību.
varbūtību, tā
vienlaikus raksturo arī viena konkrēta 2 x 2 sadalījuma varbūtību.
_____________________
8 Skat. Mothers J. Previsions et decisions
statistiques dans L'entreprise. - Paris,
1962. tulk. krievu val.: Vjn :. Cnfnbcnbxtcrbt ghtldbltybz b htitybz yf ghtlghbznbb. - V:
1966. - 512 c. (c. 208. - 209.).
Šādu varbūtību,
izmantojot kombinatoriku, var izskaitļot ar formulu
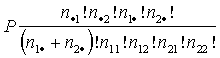 . (15.24.)
. (15.24.)
Ja iespējamo ![]() vērtību skaits nav
liels, visas varbūtības var aprēķināt skaitliski. Citos uzdevumos neliels
iespējamo vertību skaits var būt
vērtību skaits nav
liels, visas varbūtības var aprēķināt skaitliski. Citos uzdevumos neliels
iespējamo vertību skaits var būt ![]() ,
, ![]() . Konkrētajā uzdevumā
. Konkrētajā uzdevumā ![]() var būt skaitļi 0; 1;
2;
var būt skaitļi 0; 1;
2;
3. Pārējie trīs
skaitļi četrlauciņu tabulā seko automātiski.
Skaitliskie aprēķini ir šādi
|
0 |
50 |
|
|
3 |
67 |
|
|
1 |
49 |
|
|
2 |
68 |
|
|
2 |
48 |
|
|
1 |
69 |
|
|
3 |
48 |
|
|
0 |
70 |
|
Aprēķināto četru
varbūtību summa ir 1.
Jāatzīmē, ka
skaitļu, kuri lielāki par 69, faktoriālus ar parastiem skaitļotājiem tieši
izrēķināt nevar. Skaitļošanas grūtības var pārvarēt, izteiksmes logaritmējot un
faktoriālu logaritmus nolasot speciālās tabulās.
Konkrētajā gadījumā
ir iespējams faktoriālus saīsināt un izskaitļot tieši.
Piemēram
![]()
Ja no divu
piegādātāju 120 partijām 3 ir izbrāķētas, turklāt izbrāķēto partiju sadalījums
starp piegādātājiem ir nejaušs, tad varbūtība, ka pirmajam piegādātājam
izbrāķēto partiju nebūs, ir 0,195; ka būs viena izbrāķēta partija - 0,430;
divas - 0,305. Visas tās ir pietiekami lielas, lai tādu iznākumu varētu vērtēt
kā nejaušu. Vienīgi, ja visas trīs izbrāķētās partijas būtu no pirmā
piegādātāja, šādu rezultātu jau būtu grūti izskaidrot ar nejaušību: varbūtība,
ka tāds rezultāts radies nejauši, ir 0,07.
Ja turpretī trīs
brāķa partijas būtu piegādājis otrais piegādātājs, bet pirmais nevienu (p =
0,195), tad analogu secinājumu ar pietiekoši augstu varbūtību vēl nevarētu
izdarīt, jo otrais piegādātājs ir piegādājis lielāku skaitu partiju, tādēļ arī
nejauši iespējamo izbrāķēto partiju skaits var būt lielāks.
Tāds izbrāķēto
partiju sadalījums starp piegādātājiem, kāds dots uzdevumā, ir sagaidāms ar
varbūtību 0,43, tātad ar samērā lielu, un šādu sadalījumu var uzskatīt par
nejaušu. No produkcijas kvalitātes viedokļa abi piegādatāji joprojām jāvērtē kā
līdzvērtīgi.
15.6. Rangu kritēriji
15.6.1. Divu savstarpēji neatkarīgu
izlašu salīdzināšana ar U kritēriju
U kritērijs izstrādāts Vilkoksona, Manna, Vitneja darbos
un bieži literatūrā tiek saukts viņu vārdos. Ar U kritēriju pārbauda nulles hipotēzi, ka divas neatkarīgi veidotas
izlases pieder vienai un tai pašai ģenerālkopai. Citā formulējumā: divām
ģenerālkopām, no kurām ņemtas divas izlases, ir vienādi sadalījumi. Pēdējais
apgalvojums satur arī apgalvojumu, ka
šīm ģenerālkopām ir vienādas mediānas un vidējie. Tas ļauj izteikt pirmo
apgalvojumu, ka abas ģenerālkopas var apvienot un uzlūkot par vienu un to pašu
ģenerālkopu.
Daži autori uzskata, ka U kritērijs ir pats drošākais neparametriskais kritērijs9.
U kritērijs pieder rangu kritērijiem un ir analogs t kritērijam, kuru izmanto, piemēram,
divu vidējo starpības nozīmības pārbaudei ar parametriskām metodēm.
15.6.1. Uzdevums. Firma savu izstrādājumu realizē deviņos vispārēja
rakstura un septiņos specializētos veikalos. Visi veikali atrodas vienā
pilsētā, izstrādājums paredzēts ilgstošai lietošanai, tādēļ veikala atrašanās
vietai nav izšķirošas nozīmes. Firmas vadība vēlas uzzināt, vai pircēji šo
izstrādājumu labprātāk iegādājas vispārēja rakstura, vai speciālizētos
veikalos. Lai to noskaidrotu, ir savākti dati par minētā izstrādājuma pārdošanu
visos veikalos zināmā laika vienībā (dienā, nedēļā, mēnesī). Sakārtojot
veikalus ranžētās rindās pēc pārdoto izstrādājumu daudzuma, ir iegūti šādi dati
(15.11. tabula).
15.11. tabula
Pārdoto
izstrādājumu skaits pa veikaliem (veikali ranžēti)
|
|
Veikalu rangs |
||||||||
|
Veikali |
1. |
2. |
3. |
4. |
5. |
6. |
7. |
8. |
9. |
|
1. Vispārējas nozīmes |
3 |
5 |
6 |
10 |
17 |
18 |
20 |
39 |
51 |
|
2. Specializētie |
7 |
14 |
22 |
36 |
40 |
49 |
52 |
- |
- |
Noskaidrot, vai pircēju izvēle par labu vienai no veikalu grupām ir
statistiski nozīmīga vai nē (vai atšķirības var izskaidrot ar nejaušību).
Pirmo priekšstatu
par tirdzniecības intensitāti abās veikalu grupās dod pārdoto izstrādājumu
skaita mediānas. Pirmajā grupā mediāna ir 5.veikala pārdoto izstrādājumu skaits
17, otrajā grupā 4.veikala pārdoto izstrādājumu skaits 36.
_________________
9 Sachs L. Statistische
Auswertungsmethoden. Dritte Auflage, 1972.
Tulk. krievu val. Pfrc K. Cnfnbcnbxtcrjt
jwtybdfybt. - V.> 1976. - c. 270. - 281.
Tā kā otrajā veikalu
grupā mediāna ir vairāk nekā divas reizes lielāka, var izdarīt empīrisku
secinājumu, ka tirdzniecības intensitāte ar firmas izstrādājumu ir lielāka
specializētajos veikalos.
To pašu rāda
arī aritmētiskie vidējie ![]() un
un ![]() .
.
Vairāk darba ir
jāveic, lai pārbaudītu tirdzniecības intensitātes atšķirības nozīmību abās
veikālu grupās. Šim nolūkam izmantosim
Vilkoksona - Manna - Vitneja jeb U kritēriju. Tas pārbauda pašu
sadalījumu atbilstību, vienlaikus pārbaudot arī to lokācijas, piem., mediānu
atbilstību.
Lai pārbaudītu
nulles hipotēzi, kas apgalvo, ka abu grupu sadalījumi ir vienādi, resp., abas
izlases ir ņemtas no vienas ģenerālkopas, ir jāizdara šādas darbības:
1.
Jāaprēķina empiriskie U lielumi.
2.
Jānolasa matemātiskajās tabulās U
kritiskā vērtība, atbilstoši izvēlētajam nozīmības
līmenim un novēroto vienību skaitam.
3.
Jāpieņem lēmums par hipotēzi.
1. Lai aprēkinātu U kritērija empīrisko lielumu, abu
salīdzināmo grupu vienības (veikalus) apvieno un ranžē kopējā rindā un saskaita
rangus katrai grupai atsevišķi. (15.12. tab.)
15.12. tabula
Darba
tabula empīriskā U kritērija
aprēķināšanai
|
Novērojumi |
3 |
5 |
6 |
7 |
10 |
14 |
17 |
18 |
20 |
22 |
36 |
39 |
40 |
49 |
51 |
52 |
|
Rangi |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
Grupa: pirmā - A, otrā - B |
A |
A |
A |
B |
A |
B |
A |
A |
A |
B |
B |
A |
B |
B |
A |
B |
|
Rangi 1.grupā |
1 |
2 |
3 |
|
5 |
|
7 |
8 |
9 |
|
|
12 |
|
|
15 |
|
|
Rangi 2.grupā |
|
|
|
4 |
|
6 |
|
|
|
10 |
11 |
|
13 |
14 |
|
16 |
Rangu summas pirmajā un otrajā grupā ir šādas: ![]() .
.
Var aprēķināt divus
empīriskus U lielumus
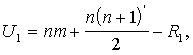 (15.25.)
(15.25.)
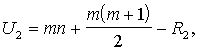 (15.26)
(15.26)
kur n un m - vienību skaits grupās.
Uzdevumā
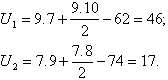
Aprēķinu pārbaudei
var izmantot sakarību
![]()
Tā kā mazāka U vērtība ved pie drošākas nulles
hipotēzes noraidīšanas, ar tabulu kritēriju salīdzina mazāko no divām aprēķinātajām U vērtībām: ![]() . Loģiski tas nozīmē pārbaudīt vienpusēju hipotēzi: tirdzniecības
intensitāte var būt lielāka vai nu specializētajos veikalos, vai abās veikalu
grupās vienādi.
. Loģiski tas nozīmē pārbaudīt vienpusēju hipotēzi: tirdzniecības
intensitāte var būt lielāka vai nu specializētajos veikalos, vai abās veikalu
grupās vienādi.
2. Lai atrastu U kritisko vērtību matemātiskajās
tabulās, ir jāizvēlas nulles hipotēzes pārbaudes nozīmības līmenis a. Pieņemot to
vienpusējam kritērijam 0,1, var izmantot šādu tabulas fragmentu (15.13.
tabula).
Par m jāpieņem lielākais, par n - mazākais novērojumu skaits
salīdzināmajās izlasēs.
Līdz ar to U ![]()
15.13. tabula
Fragments no
Vilkoksona - Manna - Vitnija U
kritisko vērtību tabulām
vienpusējam
nozīmības līmenim ![]()
(divpusējam ![]() )10
)10
|
|
n |
||||||
|
m |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
4 |
3 |
|
|
|
|
|
|
|
5 |
4 |
5 |
|
|
|
|
|
|
6 |
5 |
7 |
9 |
|
|
|
|
|
7 |
6 |
8 |
11 |
13 |
|
|
|
|
8 |
7 |
10 |
13 |
16 |
19 |
|
|
|
9 |
9 |
12 |
15 |
18 |
22 |
25 |
|
|
10 |
10 |
13 |
17 |
21 |
24 |
28 |
32 |
3. Lēmuma pieņemšana. Tā kā 17<18, ![]() nulles hipotēzi var
noraidīt ar izvēlēto varbūtību. Specializētajos veikalos tirdzniecības
intensitāte ir lielāka un intensitātes starpība ir statistiski nozīmīga.
nulles hipotēzi var
noraidīt ar izvēlēto varbūtību. Specializētajos veikalos tirdzniecības
intensitāte ir lielāka un intensitātes starpība ir statistiski nozīmīga.
Lēmuma pieņemšanas
kārtību viegli atcerēties, un arī empīriskos ![]() un
un ![]() orientējoši var
novērtēt šādi. Ja abi
orientējoši var
novērtēt šādi. Ja abi ![]() un
un ![]() ir samērā līdzīgi
skaitļi, tas norāda, ka nulles hipotēzi nevarēs noraidīt. Ja viens no viņiem ir
vairākārt lielāks nekā otrs - var prognozēt hipotēzes noraidīšanu.
ir samērā līdzīgi
skaitļi, tas norāda, ka nulles hipotēzi nevarēs noraidīt. Ja viens no viņiem ir
vairākārt lielāks nekā otrs - var prognozēt hipotēzes noraidīšanu.
Ja m un n
nav sevišķi mazi, vismaz ne mazāki
kā 8, un nav viegli pieejamas U
kritisko vērtību tabulas, tad nulles hipotēzes pārbaudei var izmantot arī
normālā sadalījuma tabulas. Šajā nolūkā aprēķina empīrisko t vērtību
__________________
10 Plašākas tabulas skat. Pfrc K. Cnfnbcnbxtcrjt
jwtybdfybt. - V.> 1976. - c. 272. - 277.
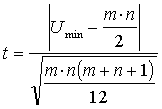 (15.27)
(15.27)
Uzdevumā
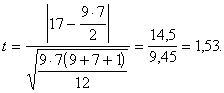
Atrasto t var uzlūkot kā standartizētu normālā
sadalījuma argumentu. Varbūtību, ka normālais sadalījums pārsniegs šo
robežvērtību, var nolasīt integrālajās tabulās kā ![]() Tā ir pirmā veida
kļūdas varbūtība, ko riskējam pieļaut,
noraidot nulles hipotēzi (nozīmības līmenis). Citiem vārdiem, nulles hipotēzi
uzdevumā var noraidīt ar varbūtību 0,937. Tā ir pietiekami liela, lai hipotēzi
noraidītu. Ar abām metodēm esam ieguvuši vienu un to pašu secinājumu.
Tā ir pirmā veida
kļūdas varbūtība, ko riskējam pieļaut,
noraidot nulles hipotēzi (nozīmības līmenis). Citiem vārdiem, nulles hipotēzi
uzdevumā var noraidīt ar varbūtību 0,937. Tā ir pietiekami liela, lai hipotēzi
noraidītu. Ar abām metodēm esam ieguvuši vienu un to pašu secinājumu.
Vispār uzdevuma
saturam un priekšnoteikumiem vispiemērotākā metode ir jālieto tad, ja izvirzīto
hipotēzi nevar ne noraidīt, ne pieņemt ar ''lielu pārsvaru''. Ja dati ir tādi,
ka lēmumu var pieņemt ar ''lielu pārsvaru'', tad praktiski visas iespējamās metodes
novedīs pie viena un tā paša lēmuma.
Tādēļ, izvērtējot
praktisku uzdevumu, datus var apstrādāt ar vislabāk zināmo metodi un tad,
ja tā nedod rezultātus ar ''lielu pārsvaru'', meklēt vispiemērotāko un
jūtīgāko metodi.
15.6.2. Iedarbības efekta novērtēšana;
Vilkoksona rangu kritērijs
Metodes ilustrēšanai izmantosim 15.6.2. uzdevumu.
15.6.2.
uzdevums. Firma pārdod savus izstrādājumus
10 veikalos. Lai pievērstu pircēju uzmanību, firmas vadība izmantoja reklāmu
televīzijā. Ir savākti dati par veikalu apgrozījumiem pirms un pēc reklāmas
salīdzināmos periodos (noteiktā nedēļas dienā, nedēļā, mēnesī vai taml.) un tie
parādīti 15.14. tabulā.
15.14. tabula
Pārdoto
preču vērtība, tūkst. latu
|
|
Veikalu numuri |
|||||||||
|
|
1. |
2. |
3. |
4. |
5. |
6. |
7. |
8. |
9. |
10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Pirms reklāmas |
25 |
40 |
32 |
70 |
51 |
15 |
37 |
60 |
45 |
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Pēc reklāmas |
30 |
35 |
45 |
64 |
70 |
22 |
44 |
74 |
51 |
40 |
Noskaidrot, vai
reklāma ir bijusi iedarbīga un vai šī iedarbība ir statistiski nozīmīga.
Uzdevuma analīze un atrisinājums. Vienkāršu
empīrisku atbildi var iegūt, saskaitot apgrozījumu kopsummu pa visiem
veikaliem, pēc kuras var izrēķināt vidējo apgrozījumu vienā veikalā pirms un
pēc reklāmas. Apgrozījumu summa pirms reklāmas ir 396, bet pēc reklāmas 475,
vidēji vienā veikalā ![]() un
un ![]() .
.
Apgrozījums pēc
reklāmas ir palielinājies. Lai tāds empīriskais secinājums būtu korekts, jāseko, lai salīdzināmajos
periodos nebūtu kādas specifiskas īpatnības: svētku dienas, masu pasākumi, lai
abos periodos būtu vienādas nedēļas dienas u.t.t.
Tālāk jānoskaidro,
vai atrastā atšķirība ir statistiski nozīmīga. Lai to izdarītu, jāaprēķina
apgrozījuma izmaiņas visos veikalos (15.14. tabulas otrās un pirmās rindas
starpības), kuras ir ierakstītas 15.15. tabulas pirmajā rindā.
15.15. tabula
Darba
tabula statistiskās hipotēzes
![]() neparametriskai
pārbaudei
neparametriskai
pārbaudei
|
|
1. |
2. |
3. |
4. |
5. |
6. |
7. |
8. |
9. |
10. |
|
|
Izmaiņas |
5 |
-5 |
13 |
-6 |
19 |
7 |
7 |
14 |
6 |
19 |
79 |
|
|
1,5 |
1,5 |
7 |
3,5 |
9,5 |
5,5 |
5,5 |
8 |
3,5 |
9,5 |
x |
|
Pozitīvie rangi
|
1,5 |
|
7 |
|
9,5 |
5,5 |
5,5 |
8 |
3,5 |
9,5 |
50 |
|
Negatīvie rangi
|
|
1,5 |
|
3,5 |
|
|
|
|
|
|
5 |
Pēc pirmās rindas
kopsummas var aprēķināt vidējo efektu
vienā veikalā ![]() . Izmantojot parametrisko kritēriju, pārbaudītu, vai ar
pietiekoši augstu varbūtību var noraidīt nulles hipotēzi, kura apgalvo, ka
. Izmantojot parametrisko kritēriju, pārbaudītu, vai ar
pietiekoši augstu varbūtību var noraidīt nulles hipotēzi, kura apgalvo, ka ![]() ģenerālkopā (ja
veikalu būtu neierobežoti daudz) ir nulle, resp.
ģenerālkopā (ja
veikalu būtu neierobežoti daudz) ir nulle, resp. ![]() .
.
To pašu hipotēzi var
pārbaudīt ar neparametrisko Vilkoksona rangu kritēriju. Pēdējais ieteicams tad,
ja novirzes ![]() veido no normālā krasi
atšķirīgu sadalījumu, piemēram, daži veikali ir vairākas reizes lielāki nekā
citi, tāpat - ja novērojumu (veikalu) skaits ir mazs.
veido no normālā krasi
atšķirīgu sadalījumu, piemēram, daži veikali ir vairākas reizes lielāki nekā
citi, tāpat - ja novērojumu (veikalu) skaits ir mazs.
Lai realizētu nulles
hipotēzes pārbaudi ar Vilkoksona kritēriju, novirzes ir jasaranžē pēc to
absolūtā lieluma, piešķirot tām rangu numurus dabisko skaitļu veidā: 1, 2, 3
...
Vismazākās novirzes ![]() 15.15. tabulā 2. rindā
ir 1. un 2. veikalam. Šiem veikaliem būtu jāpiekārto rangi 1. un 2. Bet tā kā
abas novirzes ir vienādas, viņām piešķir vidējo rangu 1,5 (tabulas 3.
rinda). 3. un 4. rangs ir jāpiešķir 4.
un 9. veikalam. Ta kā atkal abas
novirzes ir vienādas, atzīmējam vidējo rangu 3,5. Tā aizpilda visu tabulas
trešo rindu.
15.15. tabulā 2. rindā
ir 1. un 2. veikalam. Šiem veikaliem būtu jāpiekārto rangi 1. un 2. Bet tā kā
abas novirzes ir vienādas, viņām piešķir vidējo rangu 1,5 (tabulas 3.
rinda). 3. un 4. rangs ir jāpiešķir 4.
un 9. veikalam. Ta kā atkal abas
novirzes ir vienādas, atzīmējam vidējo rangu 3,5. Tā aizpilda visu tabulas
trešo rindu.
Tālāk izdala
atsevišķi pozitīvos rangus (tabulas 4.rinda) un negatīvos rangus (5.rinda) un
atrod to summas (pēdējā aile). Pozitīvo rangu summu apzīmē ar ![]() , bet negatīvo - ar
, bet negatīvo - ar ![]() .
.
Aprēķināto summu
pareizību var pārbaudīt, izmantojot sakarību
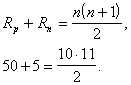
Par empīrisko
skaitli, ko izmanto hipotēzes pārbaudei, izmanto mazāko (pozitīvo vai negatīvo)
rangu summu. Uzdevumā tā ir ![]() . Nulles hipotēzi noraida, ja tā ir mazāka vai vienāda ar
kritisko robežu, kuru nolasa speciālās Vilkoksona kritērija tabulās pa pāriem
saistītu novērojumu starpībām. Neliels izvilkums no šīm tabulām ir dots 15.16.
tabulā.
. Nulles hipotēzi noraida, ja tā ir mazāka vai vienāda ar
kritisko robežu, kuru nolasa speciālās Vilkoksona kritērija tabulās pa pāriem
saistītu novērojumu starpībām. Neliels izvilkums no šīm tabulām ir dots 15.16.
tabulā.
15.16. tabula
Vilkoksona kritērijs par pa pāriem
saistītiem novērojumiem11
|
|
Vienpusējs |
Abpusējs |
||
|
n |
5 % |
1 % |
5 % |
1 % |
|
8 |
5 |
1 |
3 |
0 |
|
9 |
8 |
3 |
5 |
1 |
|
10 |
10 |
5 |
8 |
3 |
|
11 |
13 |
7 |
10 |
5 |
|
12 |
17 |
9 |
13 |
7 |
Tā kā reklāmas
rezultātā pircēju interese par preci var vienīgi uzlaboties, var izmantot
vienpusēju kritēriju. Redzam, ka, ja n = 10, tad kritiskā robeža nozīmības
līmenim 0,05 ir 10, bet nozīmības līmenim 0,01 - 5. Empīriskais ![]() , kas mazāks par
, kas mazāks par ![]() . Līdz ar to nulles hipotēzi var noraidīt ar varbūtību, lielāku
par 0,95. Bet ar varbūtību, lielāku par 0,99, to pašu hipotēzi droši noraidīt
vairs nevar, jo
. Līdz ar to nulles hipotēzi var noraidīt ar varbūtību, lielāku
par 0,95. Bet ar varbūtību, lielāku par 0,99, to pašu hipotēzi droši noraidīt
vairs nevar, jo ![]() .
.
Kā ilustratīvs
materiāls 15.4. attēlā ir parādītā
apgrozījuma noviržu ![]() diagramma (A daļa) un
rangu diagramma (B daļa).
diagramma (A daļa) un
rangu diagramma (B daļa).
Rangu sadalījumā
izteikti lielākas par ![]() ir četras novirzes,
mazākas - arī četras novirzes, bet divas novirzes ir tuvas vidējam rangam.
ir četras novirzes,
mazākas - arī četras novirzes, bet divas novirzes ir tuvas vidējam rangam.
Vērtējot apgrozījuma
noviržu sadalījumu, jāatzīmē, ka lielākas par vidējo novirzi ![]() ir četru veikalu
novirzes, kuras ir lielas. Savukārt mazākas par 7,9 ir sešas novirzes, kuras ir
salīdzinoši mazākas. Tādēļ noviržu sadalījums nav īsti tuvs normālam.
ir četru veikalu
novirzes, kuras ir lielas. Savukārt mazākas par 7,9 ir sešas novirzes, kuras ir
salīdzinoši mazākas. Tādēļ noviržu sadalījums nav īsti tuvs normālam.
15.6.3. Aproksimācija ar normālo
sadalījumu
Ja izlase, piemērā -
veikalu skaits, ir liela, izvirzīto nulles hipotēzi var pārbaudīt, izmantojot
normālo sadalījumu. Šajā gadījumā nav nepieciešams izmantot sākotnējās
novirzes, kuru sadalījums var krasi atšķirties no normālā, bet ir iespējams
empīrisko t koeficientu aprēķināt,
izejot no minimālās rangu summas ![]() (mazākās pozitīvo vai
negatīvo rangu summas). Izmanto formulu 15.28:
(mazākās pozitīvo vai
negatīvo rangu summas). Izmanto formulu 15.28:
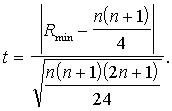 (15.28)
(15.28)
Pārejot no novirzēm
naturālā skalā uz rangiem un to novirzēm, ekstremālie novērojumi zaudē savu
ekstremālo raksturu. Zaudējot daļu informācijas, atlikusī informācija kļūst
viendabīgāka.
Empīrisko t
vērtību salīdzina ar kritisko robežvērtību sadalījuma tabulās.
Iepriekšējā uzdevumā (15.15. tabulā) n = 10, tādēļ šo metodi lietot nevajadzētu. Tomēr metodes demonstrēšanai
aprēķinus izdarīsim.
___________________
11 Plašāku tabulu skat. piem.: Pfrc K. Cnfnbcnbxtcrjt
jwtybdfybt. - c. 289.
A daļa
|
|
|
B daļa
|
|
|
15.4. attēls.
Apgrozījuma noviržu ![]() un rangu diagrammas
un rangu diagrammas
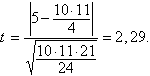
Ja grib izmantot vienpusēju kritēriju, ir jāatrod normālā
sadalījuma integrālā funkcija F(2,29) = 0,989.
Ar šādu varbūtību
var noraidīt izvirzīto nulles hipotēzi. Pirmā veida kļūdas varbūtība (nozīmības
līmenis) ir 1 - 0,989 = 0,011. Redzam, ka pat izteikti mazas izlases gadījumā
abas metodes ir devušas praktiski vienādus rezultātus.
15.7. Neparametriski sakarību rādītāji
Vienkāršas
variācijas rindas veido pēc vienas pazīmes, un metodes, kuras izmanto to
apstrādei un analīzei, sauc par viendimensijas statistikas metodēm. Ja analīzē
vienlaikus un kompleksi ir jāaplūko divas pazīmes, runā par divu dimensiju
statistikas metodēm, ja vairāk - par daudzdimensiju metodēm. Starp divu un
daudzdimensiju metodēm svarīgākās ir metodes, ar kurām skaitliski raksturo divu
(vairāku) statistisku pazīmju sakarības.
Parametriskās
statistikas ietvaros statistisko sakarību pētīšanai visbiežāk izmanto
regresijas un korelācijas analīzi, kuru pamatā ir vismazāko kvadrātu metode.
Tādēļ
neparametriskās statistikas uzdevums ir izstrādāt metodes un rādītājus, kuri
saturētu regresijas un korelācijas koeficientiem līdzīgu informāciju, bet
nebūtu saistīti ar korelācijas un regresijas analīzei izvirzāmiem
priekšnoteikumiem.
15.7.1. Spirmena un Kendela rangu
korelācijas koefiecinti
15.7.1. Uzdevums. Inženieris, kura darbs saistīts ar gāzes piegādi
dzīvokļu apsildīšanai, vēlas noskaidrot, kā gaisa temperatūra ietekmē gāzes patēriņu. Šim nolūkam viņš ir
savācis datus par gada 10 mēnešiem
(15.17. tabula).
15.17. tabula
Atmosfēras
temperatūra un gāzes patēriņš apsildināšanai
|
Mēnesis |
Gaisa temperatūra grādos, x |
Gāzes patēriņš, milj. m3 ,
y |
|
Oktobris |
10,7 |
18,3 |
|
Novembris |
5,2 |
40,1 |
|
Decembris |
3,6 |
50,3 |
|
Janvāris |
3,5 |
46,1 |
|
Februāris |
3,5 |
44,5 |
|
Marts |
8,6 |
30,2 |
|
Aprīlis |
13,0 |
10,9 |
|
Maijs |
16,2 |
5,5 |
___________________
12 Datu avots. Vjn :. Cnfnbcnbxtcrbt ghtldbltybz b htitybz yf
ghtlghbznbb. Gth. c ahfyw. -
V. Ghjuhtcc> 1966.-c. 297.
Vizuālu priekšstatu
par sakarību esamību un to raksturu var iegūt, izgatavojot korelācijas
diagrammu (15.5. att.)
|
|
15.5. attēls. Gāzes
patēriņa y izmaiņas mainoties gaisa temperatūrai x
Pēc attēla ir
redzams, ka punkti, skatoties no kreisās puses uz labo, ir novietoti arvien
tuvāk abscisu asij. Tas nozīmē, ka pazīmes
x un y saista negatīva sakarība. Pēc samērā maza novērojumu skaita diezgan grūti pateikt, kādā mērā izpildās
klasiskās regresijas un korelācijas analīzes priekšnoteikumi.
Izmantojot klasisko
metodi, iegūstam, ka sakarības raksturo regresijas vienādojums. ![]() un korelācijas
koeficients r = - 0,988.
Paagstinoties atmosfēras temperatūrai par 1 c, gāzes patēriņš šajā rajonā
samazinās vidēji par 3,48 milj.m3. Sakarības ir ļoti ciešas, par ko
liecina korelācijas koeficients, kurš ir tuvs vienam.
un korelācijas
koeficients r = - 0,988.
Paagstinoties atmosfēras temperatūrai par 1 c, gāzes patēriņš šajā rajonā
samazinās vidēji par 3,48 milj.m3. Sakarības ir ļoti ciešas, par ko
liecina korelācijas koeficients, kurš ir tuvs vienam.
Tālāk iedomāsimies,
ka vēl ir novērojumi par vienu mēnesi, kurā ![]() (attēlā šis novērojums
attēlots ar aplīti). Ir redzams, ka šis novērojums krasi atšķiras no pārējiem.
Tas var būt radies objektīvu apstākļu dēļ (liela avārija gāzes padeves sistēmā,
kas neļāva piegādāt temperatūrai atbilstošo daudzumu) vai vienkārši kādu
statistiskās novērošanas kļūdu dēļ.
(attēlā šis novērojums
attēlots ar aplīti). Ir redzams, ka šis novērojums krasi atšķiras no pārējiem.
Tas var būt radies objektīvu apstākļu dēļ (liela avārija gāzes padeves sistēmā,
kas neļāva piegādāt temperatūrai atbilstošo daudzumu) vai vienkārši kādu
statistiskās novērošanas kļūdu dēļ.
Tā vai citādi šis
novērojums neiekļaujas vispārējā likumsakarībā. Ja krasi atšķirīgo novērojumu
paturam datu masīvā un to no jauna apstrādājam ar vismazāko kvadrātu metodi,
tad iegūstam ![]() , kas ievērojami atšķiras no sakarībām kopas pamatmasā.
, kas ievērojami atšķiras no sakarībām kopas pamatmasā.
Šajā un līdzīgos
gadījumos ir jālemj vai nu krasi atšķirīgos novērojumus pirms datu apstrādes
anulēt vai arī precīzāko parametrisko metožu vietā lietot neparametriskās,
kuras ir mazāk jūtīgas pret krasi atšķirīgiem novērojumiem un vispār pret
sadalījuma novirzi no normālā (šoreiz no divu dimensiju normālā sadalījuma).
No neparametriskiem
sakarību ciešuma rādītājiem ērti lietot Spirmena
rangu korelācijas koeficientu. To aprēķina ar formulu
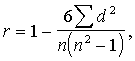 (15.29)
(15.29)
kur d -
starpība starp faktorālās un rezultatīvās pazīmes rangiem jeb x un y
skaitlisko lielumu kārtas numuriem.
Ja neizmanto datoru
vai programmējamu skaitļotāju, jāsagatavo darba tabula (15.18. tabula.).
15.18. tabula
Darba
tabula Spirmena rangu korelācijas koeficienta aprēķināšanai
|
Novērojumu Nr. |
|
|
Novērojumu rangi pēc |
Rangu starpība |
Rangu starpības |
|
|
|
x |
y |
x |
y |
d |
kvadrāts |
|
|
|
|
|
|
|
|
|
1 |
10,7 |
18,3 |
6 |
3 |
3 |
9 |
|
2 |
5,2 |
40,1 |
4 |
5 |
-1 |
1 |
|
3 |
3,6 |
50,3 |
3 |
8 |
-5 |
25 |
|
4 |
3,5 |
46,1 |
1,5 |
7 |
-5,5 |
30,25 |
|
5 |
3,5 |
44,5 |
1,5 |
6 |
-4,5 |
20,25 |
|
6 |
8,6 |
30,2 |
5 |
4 |
1 |
1 |
|
7 |
13,0 |
10,9 |
7 |
2 |
5 |
25 |
|
8 |
16,2 |
5,5 |
8 |
1 |
7 |
49 |
|
|
|
|
|
|
|
|
|
K o p ā |
x |
x |
x |
x |
x |
160,5 |
![]()
Spirmena rangu
korelācijas koeficients arī norāda uz ciešām, negatīvām sakarībam.
Pievienojot vienu
neraksturīgu novērojumu, Spirmena rangu korelācijas koeficients pēc absolūtas
vērtības m samazinās no 0,911 līdz
0,888, kamēr parastais jeb Pirsona korelācijas koeficients - no 0,988 līdz
0,864. Uzdevums parādīja, ka neparametriskais rādītājs ir mazāk jūtīgs pret
neraksturīgiem novērojumiem.
Kā alternatīvu
neparametrisku sakarību ciešuma rādītāju var izmantot Kendela rangu korelācijas koeficientu u.c.
Lai aprēķinātu
Kendela rangu korelācijas koeficientu, novērojumu sakārto pēc pirmās pazīmes rangiem un izraksta atbilstošā
secībā otrās pazīmes rangus. Pēc 15.18. tabulas datiem iegūstam:
|
x |
1,5 |
1,5 |
3 |
4 |
5 |
6 |
7 |
8 |
|
y |
7 |
6 |
8 |
5 |
4 |
3 |
2 |
1 |
Tālāk apstrādājam
tikai otrās pazīmes rangus. Pirmā
novērojuma otrās pazīmes rangs ir 7.
Saskaitām, cik šim skaitlim labajā pusē ir lielāku rangu
par 7 . Tāds ir viens. Pierakstām
nelielā darba tabuliņā:
|
+ |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
P = 2 |
|
- |
6 |
5 |
5 |
4 |
3 |
2 |
1 |
Q = 26 |
Saskaitām, cik pa
labi no 7 ir mazāki rangi. Tādu ir 6. Ierakstām šo skaitli darba tabuliņas
otrajā rindā. Tāpat apstrādājam otro novērojumu, kura otrās pazīmes rangs ir 6.
Pa labi no 6 ir viens lielāks un 5 mazāki rangi. Ierakstām šos skaitļus darba
tabuliņā.
Nākošo izvērtējam
trešo novērojumu. Pa labi no 8 lielāku skaitļu nav, bet ir pieci mazāki
skaitļi.
Līdzīgi apstrādājam
visus parējos novērojumus. Aprēķinu pareizību kontrolē tā, ka katra nākošā
novērojuma ''plus'' un ''mīnus'' skaitļu summa ir par vienu mazāka nekā
iepriekšējā.
Visu ''plus''
skaitļu summu M.Kendels apzīmē ar P,
bet ''mīnus'' skaitļu summu ar Q. Kad
tās ir saskaitītas, var aprēķināt Kendela rangu korelācijas koeficientu pēc
formulas
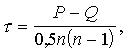 (15.30)
(15.30)
kur n -
novērojumu skaits.
Uzdevumā
![]()
M.Kendels parāda, ka
aprēķinu var vienkāršot saskaitot tikai par kārtējo lielāko rangu skaitu. Tad
izmanto formulu
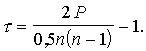 (15.31)
(15.31)
Uzdevumā
![]()
Kendela rangu
korelācijas koeficients kļūst nedaudz nenoteikts, ja novērojumiem ir piešķirti
dalīti rangi, kā tas ir arī 15.18. tabulā pazīmei x.
Rangu korelācijas
koeficientus visplašāk izmanto, izvērtējot, cik saskaņoti darbojas dažādas
ekspertu komisijas, kuru locekļi dod novērošanas vienībām savus subjektīvos
novērtējumus, piemēram, izliek atzīmes vai saranžē sportistes mākslas
vingrošanā.
15.7.2. Kontingences koeficients
Ja vismaz viena no
savstarpēji saistītām pazīmēm ir atributīva (jēdzieniska) vai citādi metriski
nesamērojama, tad ne parasto Pirsona, ne rangu korelācijas koeficientu
aprēķināt nevar. Šādos gadījumos divu pazīmju sakarību ciešumu var raksturot,
izmantojot kādu kontingences koeficientu.
15.7.2. Uzdevums. Daļa no studentiem
pirms iestāšanas augstskolā ir strādājuši. Noskaidrot, vai pirmsstudiju
nodarbošanās raksturs ir statistiski saistīts ar sekmību augstskolā. Ir
sakopoti dati, kuri parādīti 15.19. tabulā.
15.19. tabula
Studentu
sadalījums pēc pirmsstudiju nodarbošanās un sekmības augstskola13
|
Pirmsstudiju |
Studentu |
Studentu skaits ar
vidējo atzīmi eksāmenu sesijā |
||||
|
nodarbošanās |
skaits |
līdz 3,49 |
3,5 -3,99 |
4,0 - 4,49 |
4,5 - 4,99 |
5,0 |
|
|
|
|
|
|
|
|
|
Strādnieks |
210 |
26 |
66 |
72 |
33 |
13 |
|
Laukstrādnieks |
29 |
4 |
9 |
13 |
3 |
0 |
|
Ierēdnis bez spe- ciālās izglītības |
269 |
16 |
55 |
110 |
69 |
19 |
|
Ierēdnis ar spe- ciālo izglītību |
152 |
8 |
27 |
56 |
50 |
11 |
|
Karavīrs |
79 |
8 |
22 |
34 |
14 |
1 |
|
Sagatavošanas nodaļas klausītājs |
224 |
40 |
75 |
85 |
19 |
5 |
|
|
|
|
|
|
|
|
|
K o p ā - Skaits |
963 |
102 |
254 |
370 |
188 |
49 |
Pirmsstudiju
nodarbošanās ir atributīva pazīme; tās nozīmes (nodarbošanās veidus) nevar
ranžēt. Arī atzīmes sesijā tikai nosacīti var uzlūkot par kvantitatīvi
samērojamām. Par atzīmēm piecu ballu sistēmā nav īsti zināms, vai atzīme
''teicami'' atspoguļo tikpat pārākas zināšanas, salīdzinot ar ''labi'', kā
''labi'', salīdzinot ar ''apmierinoši''.
Tādēļ sakarību
ciešumu starp pirmsstudiju nodarbošanos un sekmību augstskolā raksturosim ar
kontingences koefiecientu.
Ir dažādi
kontingences koeficienti: tetrahorie, polihorie, Čuprova, Pirsona, parastie un
entropijas; aprēķinos var izmantot absolūtos un relatīvos biežumus.
Tā kā uzdevumā
(15.19. tabula) ir vairāk nekā 2 x 2 grupas, jāizmanto polihorais koeficients.
Aprēķināsim Pirsona koeficientu tieši no absolūtajiem biežumiem, jo tas ir
vienkāršāk.
Tādā gadījumā ir
jāizmanto formula
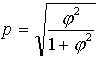 , (15.32)
, (15.32)
kur:
p - Pirsona polihorais kontingences
koeficients,
___________________
13 Šī ir viena no daudzfāzu izlases fāzēm. Tajā
ieteverti tie studenti no primārās izlases (4420),
kuriem ir
bijusi pirmsstudiju nodarbošanās bez mācībām vidusskolā. Avots:
I.Ciemiņa,
O.Krastiņš.
Kontingences koeficienti - R.: LU, - 1991. - 6.lpp. Tur arī kontingences
koeficienti
aplūkoti plašāk.
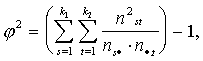
kur savukārt:
![]() - vienību skaits s rindiņā (grupā pēc pirmās pazīmes) un t ailē
- vienību skaits s rindiņā (grupā pēc pirmās pazīmes) un t ailē
(grupā pēc otrās pazīmes);
![]() un
un ![]() - vienību skaits
marginālo kopsummu rindā un ailē
- vienību skaits
marginālo kopsummu rindā un ailē
(punkts nozīmē, ka attiecīgā
indeksa nav);
![]() un
un ![]() - grupu skaits pēc
pirmās un otrās pazīmes.
- grupu skaits pēc
pirmās un otrās pazīmes.
Strādājot ar neprogrammējamu
skaitļotāju, ir jāizmanto un jāizskaitļo šāds polinoms:
![]()
(pavisam 31 saskaitāmais).
Līdz ar to Pirsona
kontingences koeficients ir
![]()
Ja aprēķinātais
lielums būtu korelācijas koeficients, sakarības vērtētu kā vājas, tikko
manāmas. Korelācijas koeficientam ir īpašība, pieaugot sakarību ciešumam,
sākumā pieaugt ļoti strauji (apmēram līdz 0,5 - 0,6), tālāk - lēni (apmēram
līdz 0,8) un visbeidzot tikko manāmi (robežās no 0,9 līdz 1). Kontingences
koeficients, pieaugot sakarību ciešumam, palielinās vienmērīgāk. Tādēļ
kontingences koeficients 0,286 raksturo jau vidēji ciešas sakarības.
Ja aprēķina citu -
entropijas kontingences koeficientu divu dimensiju normālam sadalījumam (mūsu
uzdevumā sadalījums nevar būt normāls, jo tas nemaz nav kvantitatīvs), tad var
atrast ekvivalentu korelācijas koeficientu, kurš raksturo tikpat ciešas sakarības.
Piemēram, entropijas kontingences koeficientam 0,30 ir ekvivalents korelācijas
koeficients 0,58. Par parasto kontingences koeficientu šāda salīdzināšanas
metode nav zināma.
15.7.3. Teila regresijas koeficients
Ja pētējot sakarības
nepietiek ar sakarību ciešuma rādītājiem, bet ir vajadzīgs noskaidrot, kā
faktorālās izmaiņas kvantitatīvi ietekmē rezultatīvo pazīmi, arī šo uzdevumu
var atrisināt ar neparametriskām metodēm. To, piemēram, var izdarīt ar Teila
metodi, aprēķinot koeficientu, kurš pēc satura ir līdzīgs parastajam vienkāršas
lineāras regresijas koeficientam. Metode prasa, lai abas saistītās pazīmes būtu
kvantitatīvas, t.i., metriski samērojamas.
15.7.3. uzdevums. Firma izgatavo plastmasas tilpnes, presējot zem
spiediena. Produkcijas kvalitātes statistika bija novērojusi, ka svārstās
defektīvo izstrādājumu īpatsvars tādēļ, ka neiznāk vienāds trauku sieniņu
biezums. Speciālisti izteica domu, ka to varētu radīt gaisa spiediena
svārstības presē. Lai pārbaudītu šo pieņēmumu, trīs mēnešu laikā reģistrēja
gaisa spiedienu presē un defektīvo izstrādājumu īpatsvaru procentos. Ņemam mazu
izlasi no tādējādi iegūtajiem datiem un aprēķināsim, par cik procentiem vidēji
pieaug brāķa īpatsvars, pieaugot spiedienam presē par 1 kg/m2
(15.20. tabula).
15.20.
tabula
Izlases
dati tehnoloģisku sakarību pētīšanai14
|
Novērojuma Nr.1 |
1 |
2 |
3 |
4 |
5 |
|
Spiediens kg/cm2 x |
8,6 |
9,2 |
8,2 |
8,5 |
8,3 |
|
Brāķa izstrādājumu īpatsvars, % |
0.89 |
0.91 |
0.86 |
0.87 |
0.88 |
Izgatavojot
korelācijas diagrammu (15.6.attēls), redzam, ka pieaugot gaisa spiedienam presē
x, visumā pieaug arī brāķa izstrādājumu īpatsvars. Sakarības ir pozitīvas un
lineāras (15.6 att.) Apstrādājot datus ar vismazāko kvadrātu metodi, iegūstam
regresijas vienādojumu
![]()
un korelācijas koeficientu r = 0,910, kas norāda uz
ciešām sakarībām. Zināmas bažas rada tas, ka priekš regresijas analīzes ar
vismazāko kvadrātu metodi 5 novērojumi ir ļoti maz. Bez tam novērojums x = 9,2;
y = 0,91 (punkts attēla labajā augšas stūrī) diezgan manāmi izdalās no
pārējiem. Tādēļ apstrādāsim datus ar mazāk jūtīgām pret artefaktiem neparametriskām metodēm.
15.6. attēls.
Gaisa spiediena x ietekme uz brāķa izstrādājumu īpatsvaru y (korelācijas
diagramma)
Jau pazīstamais
Spirmena rangu korelācijas koefieicnts iznāk 0,90, kas ir ļoti tuvs parastajam
Pirsona korelācijas koeficientam - 0,91.
Tālāk aprēķināsim
regresijas koeficientu bez vismazāko kvadrātu metodes izmantošanas ar Teila paņēmienu. Lai to realizētu, ir
jāizpilda šāds algoritms.
1. Jāaprēķina
attiecības
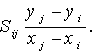 (15.33)
(15.33)
__________________
14 Datu avots: Rey' {.
Cnfnbcnbxtcrbt vtnjls gjdsitybz rfxtcndf. Gth. c fyuk. - V.%
Abyfycs b cnfnbcnbrf> 1990.-c.
89.
Ir jāprēķina m tādas attiecības, kur ![]() - visas iespējamās
kombinācijas no n novērojumiem, ņemot
tos pa divi. Būtībā ir jāatrod leņķa
koeficienti taisnēm, kas savieno katrus divus punktus korelācijas diagrammā.
Citiem vārdiem, ir it kā jātrod katriem diviem novērojumiem savi regresijas
vienādojumi, lai pēc tam atrastu šo koeficientu mediānu.
- visas iespējamās
kombinācijas no n novērojumiem, ņemot
tos pa divi. Būtībā ir jāatrod leņķa
koeficienti taisnēm, kas savieno katrus divus punktus korelācijas diagrammā.
Citiem vārdiem, ir it kā jātrod katriem diviem novērojumiem savi regresijas
vienādojumi, lai pēc tam atrastu šo koeficientu mediānu.
Ja neizmanto datoru
vai programmējamu skaitļotāju, starprezultātus ērti sakārtot tabulā 15.21.
15.21. tabula
Pāru
novērojumu regresijas koeficienti Teila metodei
|
Kombinācija
(novērojumu Nr.) |
|
|
|
|
|
|
|
|
|
1; 2 |
0,89 - 0,91 = - 0,02
|
8,6 - 9,2 = - 0,6 |
0,033 |
|
1; 3 |
0,89 - 0,86 =
0,03 |
8,6 - 8,2 = 0,4 |
0,075 |
|
1; 4 |
0,89 - 0,87 =
0,02 |
8,6 - 8,5 = 0,1 |
0,200 |
|
1; 5 |
0,89 - 0,88 =
0,01 |
8,6 - 8,3 = 0,3 |
0,033 |
|
2; 3 |
0,91 - 0,86 =
0,05 |
9,2 - 8,2 = 1,0 |
0,050 |
|
2; 4 |
0,91 - 0,87 =
0,04 |
9,2 - 8,5 = 0,7 |
0,057 |
|
2; 5 |
0,91 - 0,88 =
0,03 |
9,2 - 8,3 = 0,9 |
0,033 |
|
3; 4 |
0,86 - 0,87 = - 0,01 |
8,2 - 8,5 = - 0,3 |
0,033 |
|
3; 5 |
0,86 - 0,88 = - 0,02 |
8,2 - 8,3 = - 0,1 |
0,200 |
|
4; 5 |
0,87 - 0,88 = - 0,01 |
8,5 - 8,3 = 0,2 |
- 0,050 |
2. Atrastās ![]() vērtības jāranžē,
ņemot vērā algebriskās zīmes:
vērtības jāranžē,
ņemot vērā algebriskās zīmes:
- 0,050; 0,033; 0,033; 0,033; 0,033; 0,050;
0,057; 0,075; 0,200; 0,200.
3. Jāatrod ![]() mediāna. Tā kā mums ir
pārskaitlis,
mediāna. Tā kā mums ir
pārskaitlis, ![]() vērtību, mediānu atrod
kā
vērtību, mediānu atrod
kā
divu ranžētās rindas vidū esošo skaitļu vidējo:
![]()
Tas arī ir
regresijas koeficienta neparametriskais vērtējums. Viņš ir ļoti tuvs ar
vismazāko kvadrātu metodi iegūtajam vērtējumam 0,045.
Konkrētajā uzdevumā
Teila regresijas koeficienta ģeometriskā interpretācija ir diezgan sarežģita.
Vispirms tādēļ, ka mediāna bija jāprēķina kā divu ![]() vērtības locekļu
vidējais, un bez tam sakarā ar to, ka viens no šiem locekļiem 0,033 atkārtojas
4 reizes. Ja novērojumu skaits būtu nepāraskaitlis un mediāna iznāktu 0,050
(sestais skaitlis rindā), tad Teila regresijas koeficientu noteiktu tikai divi
punkti korelācijas diagrammā - otrais un trešais, kuri attēlā ir savienoti ar
līniju. Vienīgi sagadīšanās dēļ tie ir vistālāk viens no otra.
vērtības locekļu
vidējais, un bez tam sakarā ar to, ka viens no šiem locekļiem 0,033 atkārtojas
4 reizes. Ja novērojumu skaits būtu nepāraskaitlis un mediāna iznāktu 0,050
(sestais skaitlis rindā), tad Teila regresijas koeficientu noteiktu tikai divi
punkti korelācijas diagrammā - otrais un trešais, kuri attēlā ir savienoti ar
līniju. Vienīgi sagadīšanās dēļ tie ir vistālāk viens no otra.
Pētījums būtu
jāturpina, pārliecinoties, vai tik mazs novērojumu skaits, kāds bija uzdevumā,
ļauj uzskatīt, ka atklātās sakarības ir statistiski nozīmīgas. Tam nolūkam
jāpārbauda nulles hipotēze vai nu par korelācijas, vai regresijas koeficientu.
Ja to izdodas noraidīt, tad būtu lietderīgi veikt jaunu eksperimentu,
noskaidrojot kā spiediens presē ietekmē nevis brāķa procentu, bet tieši
interesējošo tilpņu sienu biezumu. Tā rezultātā, ņemot vērā sienu projekta
biezumu, varētu noteikt optimālo gaisa spiedienu presē, kurš, eksperimentu
sākot, acīmredzot ir bijis nedaudz par lielu un nestabilu.
Vēl jātzīmē, ka, palielinot novērojumu skaitu, strauji
pieaug aprēķināmo attiecību ![]() skaits. Ja vien
neizmanto datoru un speciālu programmu, Teila metode kļūst ļoti darbietilpīga.
skaits. Ja vien
neizmanto datoru un speciālu programmu, Teila metode kļūst ļoti darbietilpīga.