4. Normālais sadalījums
4.1.
Normālā sadalījuma funkcijas un grafiskie attēli
4.1.1.
Diferenciālā un integrālā funkcija, to grafiskie attēli
Dabas
un sociālajās zinātnēs pētāmie objekti un parādības parasti veido sadalījumus
ar izteiktu vienību koncentrāciju sadalījuma centrā. Izdarot grupēšanu pēc
pētāmās pazīmes un izgatavojot tam
atbilstošo stabiņu diagrammu (histogrammu), iegūstam raksturīgu piramīdveida
figūru. Ja novērojumu skaits ir liels un grupēšanas intervāli mazi, šī piramida
tuvojas īpašai figūrai, ko ierobežo zvanveida līkne, t.s. Gausa līkne. Tas ir normālā sadalījuma
diferenciālās funkcijas grafiskais attēls (skat. 4.1. attēlu). Tātad normālais
sadalījums ir robeža, uz kuru tiecas daudzi empīriskie sadalījumi. Normālo sadalījumu var uzlūkot par šo empīrisko
sadalījumu matemātisko modeli.
Empīriskā
sadalījuma uzkrāto biežumu stabiņu diagrammas virsotnes, savukārt, labi
apraksta īpaša S veida līkne, kas ir normālā sadalījuma integrālā funkcija
(4.2. attēls).
Normālā
sadalījuma likumam ir fundamentāla nozīme dažādu mērījumu un citu kvantitatīvu
novērojumu kļūdu izvērtēšanā.
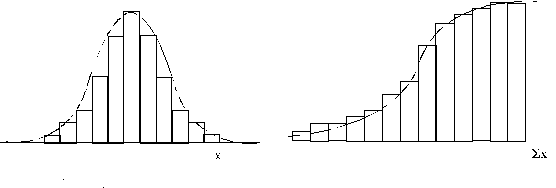
4.1.
attēls. Histogramma un normālā 4.2.
attēls. Uzkrāto biežumu diagramma
sadalījuma
diferenciālā (kumulāta) un normālā sadalījuma
funkcija integrālā funkcija
Normālā sadalījuma funkcijas vispārējā
veidā un to līknes ir šādas:
Diferenciālā funkcija : Integralā
funkcija :
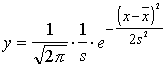
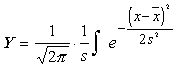 (4.1)
(4.1)
(4.2)
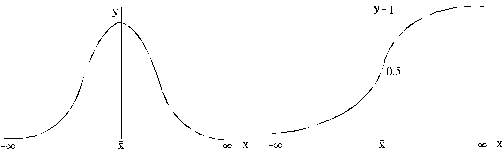
4.3. attēls. Normālā
sadalījuma diferenciālā un integrālā funkcija.
4.1.2. Normālā sadalījuma parametri
Normālā
sadalījuma funkcijās ir divi parametri,
skaitliskas konstantes, kas dažādos uzdevumos ir dažādi.
1.
![]() - gadījumlieluma vidējā
vērtība (uzdevuma robežās
konstante; dažādos uzdevumos
- gadījumlieluma vidējā
vērtība (uzdevuma robežās
konstante; dažādos uzdevumos
dažādi lielumi).
2.
s -
gadījumlieluma standartnovirze (uzdevuma robežās konstante, dažādos uzdevumos
dažādi
lielumi).
Teorētiski
![]() vietā būtu jāņem
matemātiskā cerība m un s
vietā - gadījuma lieluma standartnovirze
vietā būtu jāņem
matemātiskā cerība m un s
vietā - gadījuma lieluma standartnovirze ![]() . Praktiski pēc novērojumu datiem var izrēķināt tikai izlases
vidējo un standartnovirzi
. Praktiski pēc novērojumu datiem var izrēķināt tikai izlases
vidējo un standartnovirzi ![]() un s, tādēļ funkcijās jau ir izdarīti
attiecīgi aizvietojumi.
un s, tādēļ funkcijās jau ir izdarīti
attiecīgi aizvietojumi.
Bez
tam funkcijās ir divas universālas skaitliskas konstantes:
(naturâlo
logaritmu bâze)
![]()
x - gadījuma lieluma mainīgā vērtība
(arguments), brīvi izvēlēts lielums. Šajās funkcijās
tas ir izteikts sākotnējās skaita, svara
v.c. vienībās.
4.1.3. Normālā sadalījuma īpašības
Līdz
šim normālā sadalījuma līkni zīmējām kā vispārēju shēmu, nesaistot to ar
konkrētiem mērogiem. Ja līkni zīmē konkrētā mērogā, tad viņa ir atkarīga no
diviem sadalījuma parametriem: vidējā
lieluma ![]() un standartnovirzes s.
Šie lielumi principā var būt jebkuri skaitļi. Tie ir jāaprēķina pēc empīriskiem
datiem pirms normālā sadalījuma funkciju pierakstīšanas.
un standartnovirzes s.
Šie lielumi principā var būt jebkuri skaitļi. Tie ir jāaprēķina pēc empīriskiem
datiem pirms normālā sadalījuma funkciju pierakstīšanas.
Galvenās normālā sadalījuma īpašības
ir šādas.
1. Mainoties vidējai vērtībai ![]() , normālā sadalījuma līkne pārvietojas x
ass virzienā, saglabājot sākotnējo formu.
Ja
, normālā sadalījuma līkne pārvietojas x
ass virzienā, saglabājot sākotnējo formu.
Ja ![]() ir lielāks, līkne
atrodas vairāk pa labi, lielāko skaitļu apgabalā, un otrādi. (4.4. attēls).
ir lielāks, līkne
atrodas vairāk pa labi, lielāko skaitļu apgabalā, un otrādi. (4.4. attēls).
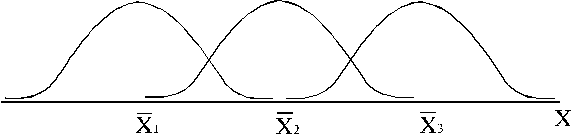
4.4. attēls. Normālā sadalījuma līknes ar dažādām vidējo
lielumu un vienādām standartnoviržu
vērtībām ![]() ; s1=s2=s3
; s1=s2=s3
2. Mainoties standartnovirzei, līknes
novietojums uz x
ass nemainās, bet mainās tās forma. Pieaugot standratnovirzei s,
samazinās līknes maksimālā ordināta, līkne itkā pieplok abscisu
asij. Samazinoties standartnovirzei,
līknes maksimālā ordināta pieaug, līkne kļūst stāvāka.
(4.5 attēls)
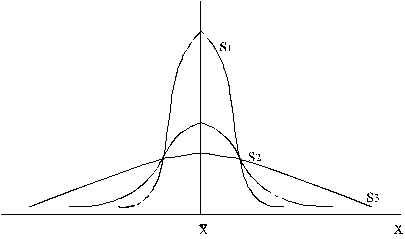
4.5. attēls. Normālā sadalījuma līknes
ar vienādām vidējo lielumu
un dažādām
standartnoviržu vērtībām : ![]() ;
; ![]() .
.
3. No iepriekšējā nevar secināt, ka,
mainot standartnovirzi, mainās līknes ekscess. Ja ekscesu mērī ar ceturtās
kārtas standartizēto momentu ![]() , tas visu laiku
paliek skaitlis 3. Šo lielumu pieņem par ekscesa
standartu. Tātad šāds ekscesa rādītājs raksturo līknes smailumu ar noteikumu, ka variācija
(standartnovirze) ir fiksēta.
, tas visu laiku
paliek skaitlis 3. Šo lielumu pieņem par ekscesa
standartu. Tātad šāds ekscesa rādītājs raksturo līknes smailumu ar noteikumu, ka variācija
(standartnovirze) ir fiksēta.
4. Normālā sadalījuma diferencialās
funkcijas līkne ir simetriska pret aritmētisko vidējo. Šī sadalījuma
asimetrijas koeficients - trešās kārtas standartizētais moments ir nulle.
5. Līknes virsotne (maksimums) atbilst
gadījumlieluma vidējai vērtībai (aritmētiskam vidējam). Ar šo lielumu sakrīt
arī sadalījuma moda un mediāna. Tā kā sadalījums ir simetrisks pret vidējo,
puse no novērojumiem ir mazāki par vidējo, puse - lielāki. Attēlā perpendikuls,
vilkts pret abscesu asi punktā ![]() , dala laukumu zem līknes divās vienādās daļās.
, dala laukumu zem līknes divās vienādās daļās.
Normālā
sadalījuma funkcijas aprēķina vai nu ar datoru, izmantojot īpašu programmu,
vai nolasa matemātiskās tabulās.
Izskaitļot
normālā sadalījuma funkcijas katram uzdevumam atšķirīgām vidējā un standartnovirzes vērtībām ir apgrūtinoši.
Sastādīt tādas normālā sadalījuma tabulas ir vienkarši neiespējami, jo ![]() un s vērtību var būt neierobežoti daudz.
un s vērtību var būt neierobežoti daudz.
Tādēļ
normālā sadalījuma funkcijas aprēķina nevis sākotnējām, bet standartizētām
gadījumlieluma vērtībām. Standartizāciju
izdara ar plaši lietoto formulu
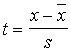 . (4.3)
. (4.3)
Kad ir noteikta vajadzīgā normalā
sadalījuma funkcija, ja uzdevuma saturs to prasa, var atgriezties pie
sākotnējām gadījuma lieluma vērtībām x,
izdarot inverso standartizāciju jeb destandartizāciju.
Varam atzīmēt vēl dažas citas normālā
sadalījuma īpašības.
6. Par standartizētu normālo
sadalījumu sauc sadalījumu, kura vidējā vērtība ir nulle, ![]() un standartnovirze -
viens, s=1. Šāda sadalījuma empirisko analogu iegūtu, zīmējot histogrammu
standartizētiem datiem. Standartizētu normālo sadalījumu apzīmē ar simbolu N
(0;1). Ja normālo sadalījumu sākotnējām x
vērtībām ir neierobežoti daudz, tad standartizēts normālais sadalījums ir viens
vienīgs. Tieši šādam sadalījumam ir sastādītas matemātiskās skaitļošanas
tabulas.
un standartnovirze -
viens, s=1. Šāda sadalījuma empirisko analogu iegūtu, zīmējot histogrammu
standartizētiem datiem. Standartizētu normālo sadalījumu apzīmē ar simbolu N
(0;1). Ja normālo sadalījumu sākotnējām x
vērtībām ir neierobežoti daudz, tad standartizēts normālais sadalījums ir viens
vienīgs. Tieši šādam sadalījumam ir sastādītas matemātiskās skaitļošanas
tabulas.
7. Normālā sadalījuma diferenciālās
funkcijas līknes pārliekuma punkti atrodas vienas standartnovirzes attālumā no
vidējā. To abscisas sākotnējā skalā ir ![]() un
un ![]() , bet standartizētā t skalā
- 1 un +1.
, bet standartizētā t skalā
- 1 un +1.
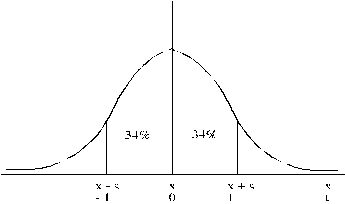
4.6.
attēls. Vienu standartnovirzi lieli apgabali zem normālā sadalījuma līknes
8. Starp perpendikuliem, kas novilkti
pret abscisu asi atbilstoši līknes pārliekuma punktiem, atrodas 68,27%
(aptuveni 68%) no laukuma zem līknes (arī no novērojumiem ģenerālkopā, ko
modelē normālais sadalījums).
Ja
novelk perpendikulus divu un triju standartnoviržu attālumā no vidējā, tad
starp tiem atrodas attiecīgi 95,45 ![]() 95% un 99,73%
95% un 99,73%
![]() 100% no laukuma zem
līknes.
100% no laukuma zem
līknes.
Šīs
īpašības ir jāizmanto, izdarot uzdevumu atrisinājumu loģisku novērtēšanu. Tāda
novērtēšana atklāj lielāko daļu iespējamo kļūdu.
4.1.4. Standartizēts normālais sadalījums
Par
standartizētu sauc normālo sadalījumu,
kura vidējais ir nulle, bet standartnovirze
- viens. Šāda sadalījuma funkcijas ir vienkāršākas nekā
iepriekš uzrādītās vispārējā gadījumlieluma funkcijas.
Diferenciālā funkcija ir šāda
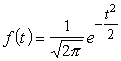 , (4.4)
, (4.4)
bet integrālā :
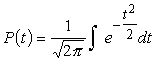 . (4.5)
. (4.5)
Diferenciālo
funkciju vajadzības gadījumā var izskaitļot. Tā ir arī tabulēta. Ja vajag
aprēķināt normālā sadalījuma līknes ordinātu, kad standartnovirze nav 1,
izmanto formulu :
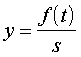 . (4.6)
. (4.6)
Nenoteiktā
integrāļa vietā lieto noteiktā integrāļa funkcijas. Tās var tabulēt, un viņas
atšķiras ar integrēšanas robežām. Grāmatās ir sastopamas trīs veidu noteiktā
integrāļa tabulas, kuras, izdarot nelielus pārrēķinus, ir savstarpēji
samaināmas.
1.
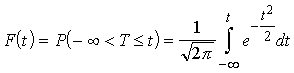 . (4.7)
. (4.7)
Tā
ir varbūtība, ka standartizēts gadījumlielums T kārtējā
izmēģinājumā iegūs vērtību no ![]() līdz t
. Ģeometriski to attēlo laukuma daļa zem normālā sadalījuma
diferenciālās funkcijas līknes no kreisa
zara līdz perpendikulam pret punktu t
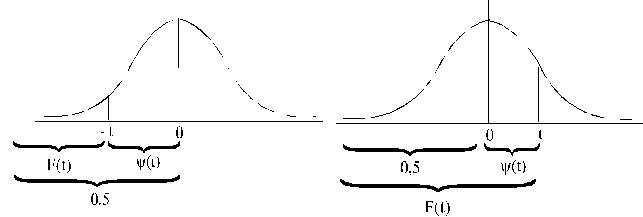
(4.7. attēla kreisā puse). Ja ir uzzīmēta integrālās
funkcijas līkne,
līdz t
. Ģeometriski to attēlo laukuma daļa zem normālā sadalījuma
diferenciālās funkcijas līknes no kreisa
zara līdz perpendikulam pret punktu t
(4.7. attēla kreisā puse). Ja ir uzzīmēta integrālās
funkcijas līkne, ![]() ir punkta ordināta, kurā
pret t vilkts perpendikuls krusto līkni
(4.7. attēla labā puse).
ir punkta ordināta, kurā
pret t vilkts perpendikuls krusto līkni
(4.7. attēla labā puse).
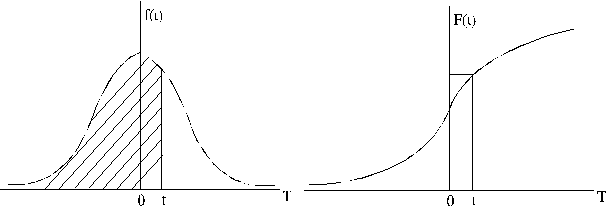
4.7.
attēls. Divas normālā sadalījuma integrālās funkcijas ģeometriskas
interpretācijas.
2.
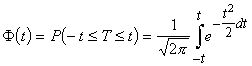 . (4.8)
. (4.8)
Tā
ir varbūtība, ka standartizēts gadījuma lielums T kārtējā
izmēģinājumā iegūs vērtību no - t
līdz +t Ģeometriski to attēlo simetriska
laukuma daļa zem līknes centra ![]() (4.8. attēls).
(4.8. attēls).
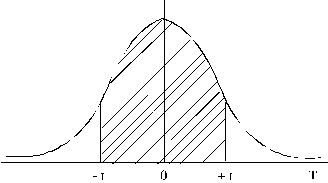
4.8.
attēls. Simetrisks pret aritmētisko vidējo laukums zem normālā sadalījuma
līknes.
3.
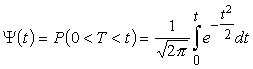 , (4.9)
, (4.9)
kura interpretācija ir analoga (4.9.
attēls).
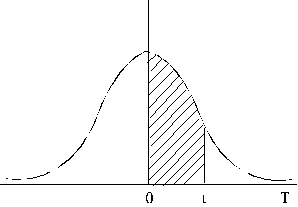
4.9.
attēls. Puse simetriska pret aritmētisko vidējo laukuma zem normālā sadalījuma
līknes.
4.2. Normālā sadalījuma lietošana
4.2.1. Tiešie uzdevumi : dotā intervāla vārbūtība
Vienkāršākie
normālā sadalījuma uzdevumi prasa atrast varbūtību, ka
gadījumlielums x atradīsies dotajā intervālā. Par tiešajiem
uzdevumiem tos sauc tādēļ, ka šādas varbūtības atrod, lietojot matemātiskās
tabulas vai programmas tiešā veidā.
1.uzdevums.
Fasēšanas
cehā iesver preci pakās pa 2 kg. Svēršanas kļūdas veido normālu sadalījumu ar
standartnovirzi 5 gr. Atrast varbūtību, ka kārtējā paka saturēs preci, kuras
neto svars nav mazāks par 1990 gr. un nav lielāks par 2010 gr.
Uzdevuma
analīze un atrisinājums.
Strādājot ar empīriskās statistikas metodēm, vajadzētu ņemt izlasi no sasvērtām
pakām, izdarīt to kontrolsvēršanu ar precīzākiem svariem, izveidot iegūto
rezultātu variācijas rindu, saskaitīt to intervālu biežumus, kas atbilst
prasītajam lielajam intervālam.
Pieņemsim, ka ir pārsvērtas 100 pakas
un iegūti šādi rezultāti (4.1 tabula un 4.10. attēls).
4.1
tabula
1. uzdevuma
empīrisks atrisinājums.
|
|
|
x |
f |
||
|
|
|
1985-1990 |
3 |
||
|
|
|
1990-1995 |
5 |
||
|
95 |
|
1995-2000 |
45 |
||
|
|
|
2000-2005 |
40 |
||
|
|
|
2005-2010 |
5 |
||
|
|
|
2010-2015 |
2 |
||
|
|
|
|
100 |
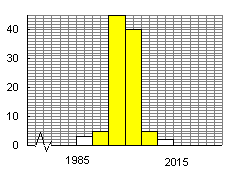
4.10.
attēls. 1. uzdevuma empīriska atrisinājuma grafisks attēls
(uzdevumam atbilstošie stabiņi svītroti)
Novērtējot
rezultātus, var secināt, ka izlasē 95% no pakām iekļaujas prasītajās svara robežās.
Ja izlase ir pietiekami reprezentatīva, var teikt, ka ar varbūtību 0,95 ir
sagaidāms, ka nejauši ņemtas pakas svars atradīsies šajās robežās. Grafiskajā
attēlā uzdevuma nosacījumiem atbilstošie stabiņi iesvītroti.
Šādai
empīriskai pieejai ir zināmi trukumi.
1. Izlase, kuru vērtējam kā
reprezentatīvu kopumā, var nebūt pietiekami reprezentatīva atsevišķās grupās.
Daži stabiņi histogrammā var būt negaidīti augsti vai zemi, salīdzinot ar
blakus esošajiem stabiņiem. Normālā sadalījuma līknes uzdevums ir izlīdzināt
šīs nejaušības.
2. Atrisinājums bija viegls tādēļ, ka
prasītais lielais intervāls veidojās no veseliem intervāliem empīriskajā
sadalījumā. Rastos nopietnas grūtības, ja uzdevumā prasītā intervāla robežas
nesakristu ar empīriskā sadalījuma intervālu robežām. Izmantojot normālo
sadalījumu, var izmantot jebkuru interesējošo intevālu (daļu zem līknes), bez
kādiem ierobežojumiem.
Tomēr
jātzīmē, ka empīrisko novērojumu dati ir
jebkuru, arī teorētisku vispārinājumu, pamats. Ja nebūtu izdarīta preču kontrolsvēršana,
no kurienes mēs uzzinātu, ka svara standartnovirze ir 5 grami?
Turpmāk
izvirzīto uzdevumu atrisināsim, izmantojot normālo sadalījumu.
Grafiski uzdevuma atrisinājums nozīmē
atrast, kāda daļa zem normālā sadalījuma līknes atrodas starp perpendikuliem,
vilktiem punktos 1990 un 2010 g.
sākotnējā svara skalā
(4.11 attēls).
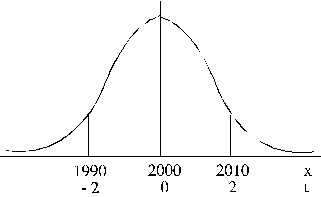
4.11.
attēls. 1. uzdevuma ar normālo sadalījumu iegūta atrisinājuma grafiska
ilustrācija.
Izpildāmās
darbības ir šādas.
1. Lai varētu izmantot normālā
sadalījuma tabulas, abi dotie kritiskie punkti ir jāstandartizē, izmantojot formulu
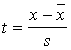 .
.
Uzdevumā bija dots, ka ![]() (normatīvais svars)
un
(normatīvais svars)
un ![]() .
.
Līdz ar to:
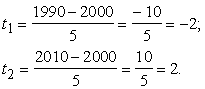
Skat. t-skalu iepriekšējā attēlā. Punktu
vietas uz abscisu ass netiek mainītas.
2. Jāatrod normālā sadalījuma
noteiktais integrāls no -2 līdz +2 (integrēšanas robežas). Tā kā abas robežas
ir simetriskas pret vidējo, atbildi var tieši nolasīt ![]() tabulās
tabulās
![]() .
.
Tā
arī ir atbilde. Ar varbūtību 0,95 var sagaidīt, ka kārtējās pakas svars būs
prasītajās robežās.
3. Citu tabulu lietošana. Ja ![]() tabulas nav
pieejamas, vai nav šīs funkcijas aprēķināšanas programma, var izmantot citas
tabulas, piem.,
tabulas nav
pieejamas, vai nav šīs funkcijas aprēķināšanas programma, var izmantot citas
tabulas, piem., ![]() tabulas, kas ļauj
atrast noteikto integrāli no -¥ līdz t.
Izskaitļojumu pamato grafiskā analīze (4.12. attēls).
tabulas, kas ļauj
atrast noteikto integrāli no -¥ līdz t.
Izskaitļojumu pamato grafiskā analīze (4.12. attēls).
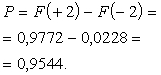
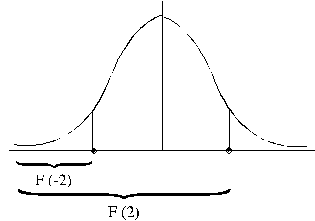
4.12.
attēls. F(t) tabulu lietošanas grafiska ilustrācija.
Rezultāti drīkst atšķirties tikai par
lietoto tabulu dažādiem noapaļojumiem.
2.
uzdevums.
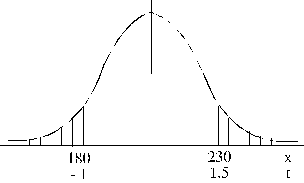
Audēju grupa, strādājot ar viena tipa
stellēm, saražo vidēji uz vienu strādnieci 200 metrus maiņā ar standartnovirzi
20 metri. Kādu var sagaidīt strādnieču sadalījumu (procentos) pēc izstrādes, ja
pieņem, ka sadalījums ir normāls.
Konkrēti:
1.
Cik procentu strādnieču noaudīs 180 - 230 m;
2.
Cik procentu strādnieču noaudīs vairāk
par 230 m;
3.
Cik procentu strādnieču noaudīs mazāk par 180 m.
Analīze un atrisinājums.
Dotie lielumi :![]() kritiskie punkti
kritiskie punkti ![]()
![]()
Droši sagaidāma notikuma varbūtība
(viens) jāsadala atbilstoši šiem punktiem trīs daļās. Ģeometriski to var
saprast kā laukuma zem normālā sadalījuma līknes sadalīšanu trīs daļās
(4.13.attēls).
|
|
(Empīriskās statistikas
analogs - biežumu summēšana
atbilstošajos histogrammas stabiņos - intervālos). Uzdevumu var interpretēt arī
tā, ka jāatrod varbūtība, ar kuru var sagaidīt, ka kārtējās strādnieces darba
ražīgums iekļausies kādā no prasītajiem intervāliem.
4.13.attēls. 2.uzdevuma grafiska
ilustrācija.
1. Lai izmantotu normālā sadalījuma
integrālās tabulas, kritisko punktu abscisas jāpārrēķina standartizētās
vienībās:
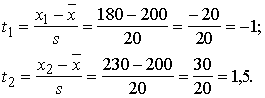
Arī tos pierakstām attēlā 4.13.
2. Tālāk var izmantot normālā
sadalījuma integralās funkcijas tabulas.
Visvieglāk atrisināt trešo jautājumu: cik strādnieču
saražos mazāk par 180 metriem? Īpasvaru viena daļās var tieši nolasīt ![]() tabulās :
tabulās :![]() .
.
Pareizinot
ar 100, iegūstam 15,87%.
Otro
jautājumu: cik strādnieču saražos vairāk par 230 metriem, var atrisināt šādi.
No pilnas iespējamo gadījumliela vērtību kopas varbūtības 1 atņem varbūtību, ka
kārtējā strādniece saražos mazāk par 230 metriem :
![]() . Pareizinot ar 100, iegūstam 6,58% .
. Pareizinot ar 100, iegūstam 6,58% .
Pirmo jautājumu var atrisināt
divējādi. Var izmantot ![]() tabulas.
tabulas.
Tad ![]() .
.
Pareizinot ar 100, iegūstam 77,45%.
Var
izmantot arī ![]() tabulas. Tad laukuma
centrālā daļa jāsadala divās daļās un tām atbilstošās varbūtības jāsummē
tabulas. Tad laukuma
centrālā daļa jāsadala divās daļās un tām atbilstošās varbūtības jāsummē
![]() .
.
Pārbaude: ![]() .
.
Pārbaude,
rēķinot ar divām dažādām tabulām, atklāj tabulu lietošanas kļūdas, bet
neatklāj kļūdas kritisko punktu un to t
vērtību noteikšanā.
4.2.2. Netiešie uzdevumi : dotās vārbūtības intervāls
Šie
uzdevumi prasa atrast kritisko robežu
(robežas), kas izdala normālā sadalījuma daļu (intervālu) atbilstoši dotai
varbūtībai. Par netiešajiem uzdevumiem tos sauc tādēļ, ka
matemātiskās tabulas, resp., programmas ir jālieto inversi (netieši).
3.
uzdevums.
Audēju
grupa, strādājot ar viena tipa stellēm, saražo vidēji uz 1 strādnieci 200
metrus maiņā ar standartnovirzi 20 metri.
Aprēķināt,
kādā līmenī jānosaka izstrādes norma, ja vēlas, lai, nekāpinot darba razīgumu,
to varētu izpildīt 90% audēju.
Analīze.
Dots,
ka ![]() un
un ![]() . Šoreiz nav
jāapreķina varbūtība, bet tā ir dota: varbūtība, ka strādniece neizpildīs
normu, ir 0,1 (10%). Ir jāaprēķina kritiskais punkts (metri), kas atbilst šādai
varbūtībai.
. Šoreiz nav
jāapreķina varbūtība, bet tā ir dota: varbūtība, ka strādniece neizpildīs
normu, ir 0,1 (10%). Ir jāaprēķina kritiskais punkts (metri), kas atbilst šādai
varbūtībai.
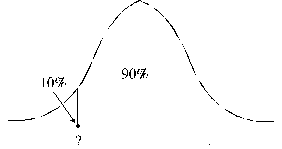
Grafiski
laukums zem normālā sadalījuma līknes jāsadala divās daļās, lai kreisajā zarā
(normas neizpildes apgabals) paliktu 10% un pārējā daļā (normas pārsniegšanas
apgabals) - 90% (4.14. attēls).
|
|
Tā kā funkcija ![]() rāda laukuma daļu pa
kreisi no t, varam rakstīt, ka ir dots
rāda laukuma daļu pa
kreisi no t, varam rakstīt, ka ir dots ![]() un meklēt, kāda
t vērtība to nodrošina.
un meklēt, kāda
t vērtība to nodrošina.
4.14.attēls. Normāla sadalījuma netiešo uzdevumu
grafiska ilustrācija (nostādne).
Atrisinājums.
1. Jāatrod t vērtība, kas nodrošina ![]() ;
; ![]() tabula jālieto
inversi. Skaitlim 0,1 tuvākais skaitlis jātrod tabulas centrālajā daļā un tam
atbilstošais t
jānolasa tabulas ieejās. Atrodam, ka t = - 1,28 (ierakstām 4.15. attēlā).
tabula jālieto
inversi. Skaitlim 0,1 tuvākais skaitlis jātrod tabulas centrālajā daļā un tam
atbilstošais t
jānolasa tabulas ieejās. Atrodam, ka t = - 1,28 (ierakstām 4.15. attēlā).
2. No standartizētām t vienībām
jāpāriet uz sākotnējām x
vienībām (metriem). To izdara, inversi lietojot standartizācijas formulu 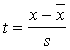 .
.
Ievietojot iegūstam ![]() ,
,
no kā var izrēķināt, ka ![]() (metri, ierakstām
4.15. attēlā).
(metri, ierakstām
4.15. attēlā).
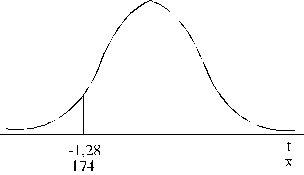
4.15.
attēls. Normālā sadalījuma netiešo uzdevumu grafiska ilustrācija
(atrisinājums).
Tātad,
nosakot izstrādes normu 174 metri, var sagaidīt, ka to izpildīs un pārsniegs
90% strādnieču. Šāda prognoze attaisnosies, ja nedarbosies faktori, kas
sistemātiski ietekmē daudzu vai pat visu strādnieču darba ražīgumu.
Tā
kā šajā uzdevumā tiklab matemātiskās tabulas kā arī standartizācijas formulu
lietojām netieši (inversi), tādus
uzdevumus sauksim par netiešiem jeb inversajiem normālā sadalījuma
uzdevumiem.
4.2.3. Normālā
sadalījuma lietošana binomiālā sadalījuma vietā
4.uzdevums
Detaļas
pēc mehāniskas apstrādes termiski norūda elektriskajā krāsnī. Vienā partijā
krāsnī ieliek 1000 detaļas. Iepriekšējā pieredze rāda, ka teicami norūdīto
detaļu (1.šķiras detaļu) iznākums ir 90%. Tātad vienas numurētas detaļas
teicamas norūdīšanas varbūtība ir 0,9.
(Uzdevuma
vienkāršošanai pieņem, ka iepriekšējās tehnoloģiskajās operācijas brāķa nav).
Aprēķināt varbūtības, ka no minētās 1000 detaļu
partijas pirmās šķiras detaļu, būs:
1)
ne mazāk kā 890 un ne vairāk kā 910;
2)
ne mazāk kā 880?
Analīze.
Uzdevuma
saturs ir formulēts tā, ka runa ir nevis par gadījumlielumu, bet par
gadījumnotikumu.
Vabūtību,
ka 1. šķiras detaļu būs ne mazāk kā 890 un ne vairāk ka 910, varētu atrast kā
šādu varbūtību summu:
![]() .
.
Summējamās
varbūtības, savukārt, varētu atrast ar Bernulli formulu. Bet tad nāktos
aprēķināt un saskaitīt 21 varbūtību. Uzdevuma otra jautājuma atrisināšanai būtu
jāaprēķina un jāsaskaita 121 varbūtība, turklāt pa kādiem apkārtceļiem
jāizvairās no ļoti lielu skaitļu faktoriālu aprēķināšanas, kas tieši nav
izdarāms.
Lai
izvairītos no ļoti lielām skaitļošanas grūtībām, uzdevumam precīzi atbilstošo binomiālo sadalījumu
aizstājam ar normālo sadalījumu. Tuvinājums ir pietiekami labs, ja
novērojumu skaits n> 50, bet
pavisam labs, ja n>100 (mums 1000).
Atrisinājuma
galvenā īpatnība būs tā, ka standartizācijas formulā ievietojamā vidējā
vērtība ![]() un standratnovirze s nav aprēķināmas parastā veidā, bet
pēc specifiskām binomiālā sadalījuma formulām
un standratnovirze s nav aprēķināmas parastā veidā, bet
pēc specifiskām binomiālā sadalījuma formulām
![]() (4.10)
(4.10)
![]() . (4.11)
. (4.11)
Atrisinājums.
Atbilstoši
binomiālā sadalījuma simboliem, ir dotas varbūtības p=0,9; q=0,1
un sērijas lielums n
=1000.
Uzdevuma
pirmajam jautājumam ir doti kritiskie punkti ![]() un
un ![]() .
.
1. Izdaram grafisko analīzi (4.16.
attēls).
|
|
Jāatrod varbūtība, kas atbilst laukuma
daļai zem normālā sadalījuma līknes starp perpendikuliem punktos m
skalā 890 un 910. Tās ir argumenta kritiskās vērtības sākotnējā m skalā.
4.16.attēls. Normāla sadalījuma lietošana
binomiālā sadalījuma
vietā.
2. Tā kā skaitļošanas tabulas ir
sastādītas argumenta standartizētām vērtībām, abas kritiskās robežas ir
jāstandartizē. Standartizācijas formulā
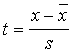
ir jāizdara šādi aizvietojumi: ![]() .
.
Iegūstam:
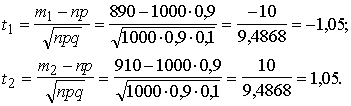
Skaidrības dēļ arī šo skalu ietveram attēlā.
3. Izmantojot matemātiskās tabulas,
jāaprēķina vajadzīgā varbūtība, resp. laukuma daļa starp perpendikuliem.
Novērtējam, kuras
tabulas ir vispiemērotākās. Tā
kā ![]() , tad var
lietot
, tad var
lietot
![]() tabulas, jo meklējamais laukums ir simetrisks pret vidējo.
tabulas, jo meklējamais laukums ir simetrisks pret vidējo.
![]() .
.
Kontrole
ar citām tabulām
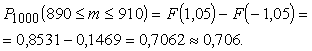
Tabulas
lietojam tieši, tādēļ uzdevumu var saukt par tiešo.
Lai
atrastu otro prasīto varbūtību, izpildām
tos pašus darbību soļus.
1. Uzzīmējam 4.17. attēlu:
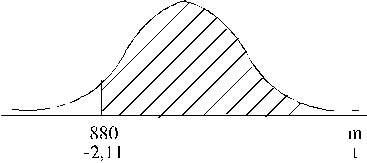
4.17.attēls.
Normālā sadalījuma lietošana binomiālā sadalījuma vietā
(otrais jautājums).
2. Izdarām kritiskā punkta
standartizāciju
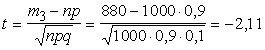 .
.
3. Jāatrod ![]() .
.
Šādu varbūtību tieši nolasīt nevar
nevienā no pieiejamām tabulām. Toties var atrast varbūtību
![]() .
.
Tā kā šī varbūtība un mūs interesejošā
varbūtība kopā dod vienu, tad meklēto varbūtību var atrast kā starpību:
![]() .
.
Ar
šādu varbūtību var sagaidīt, ka pirmās šķiras detaļu nebūs mazāk par 880.
Atrisinājuma
kontrole, izmantojot citas tabulas.
![]() .
.
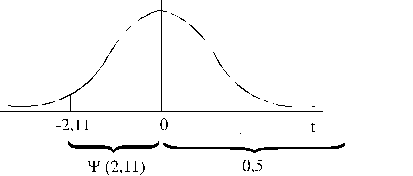
4.18.attēls.
Laukumi zem normāla sadalījuma līknes.Y(t) tabulu lietošana.
4.2.4. Normālais sadalījums produkcijas kvalitātes
kontrolei
Iepriekš
aprēķinātās varbūtības ir samērā augstas. Praktiskajā ražošanā tik stabili
rezultāti nemēdz būt. Šķietamā pretruna
izskaidrojama ar to, ka praksē nevar
nodrošināt, lai visi novērojumi (visu detaļu norūdīšanas rezultāti) būtu
savstarpēji neatkarīgi. Tādu priekšnoteikumu prasa lietotais varbūtību teorijas
modelis. Praksē nereti notiek tādas vai citādas novirzes no tehnoloģiskā
režīma, kas ietekmē visu partiju. Tad praktiskie rezultāti var būtiski
atšķirties no aprēķinātājiem. Piemēra ietvaros, izmainās kārtējās detaļas
teicamas norūdīšanas varbūtība, piem., 0,9 vietā nāk 0,8.
Tādēļ
aprēķinātās varbūtības nav fatāla garantija, ka rezultāti būs tieši tādi un ne
citādi. Tās atspoguļo vienīgi to nenoteiktību un risku, ar ko saistīta ražošana
(visu detaļu metāla masa nav ideāli
vienāda un nav vienāda viņu kustību trajektorija
krāsnī).
Tādēļ,
atrastās varbūtības un ar tām saistītās kritiskās robežas var kalpot vienīgi
tam, lai nospraustu kritērijus, kādus
darba rezultātus var uzlūkot par normāliem. Ja praktiskā
novērojumu sērija (partija) tam neatbilst, jāmeklē kādi būtiski, sistemātiski
darbojošies cēloņi, tos radījuši. Ja
novirzes ir negatīvas, trūkumi jānovērš. Ja pozitīvas, jācenšas saglabāt šīs
partijas ražošanā radušās īpatnības, jo tādējādi var uzlabot ražošanu.
No
pēdējā uzdevuma jau samērā tieši var pāriet uz t.s. kontroles
karšu ideju. Šādas produkcijas kontroles kartes sastāda un analizē
visi lielākie rūpniecības uzņēmumi. Kontroles kartes, ideja ir šāda.
Karti veido kā dinamikas rindas grafiku.
Uz horizontālās ass atliek laika skalu atbilstoši produkcijas kvalitātes
noteikšanas biežumam: dienas, stundas vai partijas. Uz vertikalās skalas atliek
novērtējamo kvalitātes rādītāju. Iepriekšējā piemērā tas bija 1. šķiras detaļu īpatsvars. Citos
gadījumos un vēl labāk izmantot kādu tieši izmērāmu rādītāju.
Kartes
maketā (sagatavē) novelk horizontālas līnijas:
1. Centrālo līniju, kas atbilst
vidējai praktiski sasniegtai produkcijas kvalitātei.
Iepriekšējā piemērā tas ir 1.šķiras detaļu
īpatsvars 0,9 jeb 90%, jeb 900 no
tūkstoša.
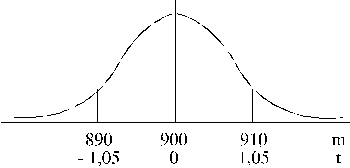
2. Divas pirmai līnijai paralēlas
līnijas pa abām pusēm no tās vienu standartnovirzi lielā
attālumā. Piemērā, ja centrālo līniju novelk atbilstoši np=900,
tad standartnovirze ir ![]() .
.
Paralēlās līnijas jāvelk 10 vienību
attālumā (890 un 910).
3. Vēl kādas citas paralēlas līnijas,
kas ietver citu, parasti lielāku daļu no laukuma zem normālā sadalījuma līknes: 90%, 95%,
99%.
Aizpildot
karti pakāpeniski, atbilstoši kvalitātes kontroles rezultātiem atliek punktus
un blakus esošos punktus savieno ar taisnes nogriežņiem.
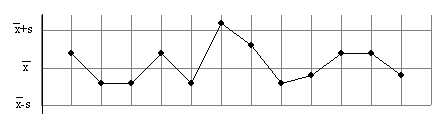
4.19.
attēls. Produkcijas kvalitātes kontrolkartes uzdevuma ilustrācija.
Lielās līnijās darba rezultātus novērtē šādi:
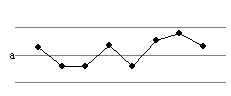
1.
Visas atzīmes kartē novietojas starp kontroles līnijam.
Rezultāti uzrāda normālu
līdz šim nenovēršamu
kvalitātes variāciju. Ražošanas process noris normāli.

2.
Atzīmes bieži nonāk
ārpus kontroles līnijām, gan
augstāk gan zemāk
par tām. Rezultātu
variācija
![]()
palielinās.
Process draud kļūt
nekontrolējams.

![]()
3. Atzīmes blīvējas zem vidus līnijas
un bieži arī nonāk
ārpus apakšējās kontroles līnijas. Ražošanas
![]() process pasliktinās. Mašīnas ir izregulējušās.
process pasliktinās. Mašīnas ir izregulējušās.
4.20. attēls. Kontrolkartes
novērtēšana.
4.2.5. Normālā sadalījuma uzdevumu klasifikācija
(kopsavilkums)
Uzdevumus,
kurus atrisina ar normālā sadalījuma palīdzību, var iedalīt divās klasēs, jeb
grupās.
1. Normālā sadalījuma patstāvīga lietošana, ja uzdevumā ir
runa par nepārtrauktu gadījumlielumu, kura sadalījums ir normāls vai tuvs tam.
2. Normālā sadalījuma lietošana binomiālā (tātad diskrēta) sadalījuma vietā,
izdarot tuvinātus aprēķinus, ja novērojumu skaits ir liels (4.uzdevums).
Starpība
ir tā, ka pirmajā gadījumā vidējo lielumu un standartnovirzi aprēķina ar
parastajām formulām
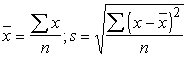 ,
,
vajadzības gadījumā izmantojot statistiskos svarus. Var
izmantot momentu formulas.
Otrajā
gadījumā šos parametrus aprēķina ar specifiskām binomialā sadalījuma formulām:
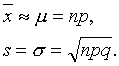
Tālākie
aprēķini abās grupās praktiski līdzīgi;
atšķiras atkal rezultātu interpretācija.
Katras
uzdevumu grupas jeb klases ietvaros izšķir divus uzdevumu tipus.
Tiešajos uzdevumos ir jāatrod
varbūtības. Tās vairāk vai mazāk tieši var nolasīt matemātiskajās tabulās. (1.,
2., 4 uzdevumi).
Inversajos
jeb netiešajos uzdevumos pēc dotām varbūtībām ir jāatrod gadījuma
lieluma robežvērtības. To var izdarīt lietojot matemātiskās tabulas inversi
(netieši; 3.uzdevums).
Noskaidrojot, kurai no grupām atbilst
risināmais uzdevums, kļūst iespējams izmantot tipveida atrisinājuma shēmu.
4.2.6. Normālā sadalījuma tabulu savstarpēja aizvietošana
Visas
normālā sadalījuma integralās funkcijas un atbilstošās matemātiskās tabulas ir
savstarpēji aizvietojamas. Piemērotāko tabulu lietošana ir saprotamāka un
ekonomē skaitļošanas darbu.
Lai
iemācītos brīvi lietot normālā sadalījuma tabulas un vajadzības gadījumā iztikt
ar tām tabulām, kuras ir pie rokas, ir svarīgi zināt dažādu noteikto integrālu
sakarības.
1. ![]() (4.12)
(4.12)
(skat. 4.21. attēlu).
Sakarība
ir spēkā tādēļ, ka normālā sadalījuma
līkne ir simetriska pret centru. Parasti tabulē
![]() tikai pozītīvām t
vērtībām.
tikai pozītīvām t
vērtībām.
2.
Jāievēro, ka ![]() (4.13)
(4.13)
jo šī funkcija ir ekvivalenta laukuma
daļai zem līknes no ![]() līdz dotajiem t .
līdz dotajiem t .
Negatīvām vērtībām tā ir mazāka par
0,5, pozitīvām - lielāka par 0,5
(loģiskā kontrole, skat. 4.22. attēlu).
3.
![]() vai
vai ![]() . (4.14)
. (4.14)
L1 = L2,
ja
ê-t ê= êt ê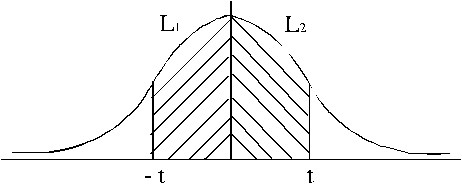
4.21. attēls. ![]() un
un ![]() tabulu lietošana.
tabulu lietošana.
Funkcija ![]() ir ekvivalenta
simetriskai laukuma daļai zem līknes tās centrā, bet
ir ekvivalenta
simetriskai laukuma daļai zem līknes tās centrā, bet ![]() šī laukuma pusei,
ņemot no perpendikula līknes centrā (pret
šī laukuma pusei,
ņemot no perpendikula līknes centrā (pret ![]() ).
).
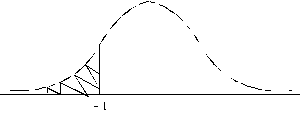
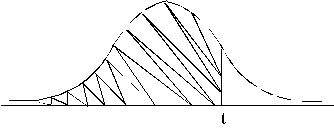
4.22.
attēls. F(t) tabulu lietošana
(4.15) (4.16)
4.
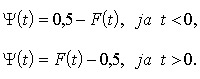
Ja viena no funkcijām ir zināma, otru
var aprēķināt ar vienkāršu darbību.
4.23.
attēls. Vajadzīgās varbūtības aprēķināšana, izmantojot divu zināmo
varbūtību (laukumu) summu vai starpību.
5. Pareizinot abas iepriekšējās
sakarības ar 2 un ņemot vērā, ka ![]() iegūstam
iegūstam
![]() (4.17)
(4.17)
![]() . (4.18)
. (4.18)
Var
pierakstīt arī vēl citas sakarības. Tās nav nepieciešams iemācīties no galvas.
Tās var viegli izdomāt, ja ir zināmas funkciju ![]() un
un ![]() integrēšanas robežas
un izprasts tām atbilstošo laukumu izvietojums zem līknes. Visbiežāk tabulē un
programmē funkciju F(t).
integrēšanas robežas
un izprasts tām atbilstošo laukumu izvietojums zem līknes. Visbiežāk tabulē un
programmē funkciju F(t).
4.2.7. Normālā sadalījuma funkciju tieša izskaitļošana
Datori
un arī programmētās vadības kalkulātori dod iespēju tieši aprēķināt normālā
sadalījuma integrālās funkcijas, neizmantojot matemātiskās tabulas. Šim nolūkam
definīcijas formulas neder. Izskaitļošanai integrāļus izvirza konverģējošās
rindās.
Piemēram
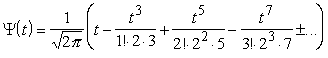 . (4.19)
. (4.19)
Šī
rinda dod labus rezultātus (ātru konverģenci),
ja t<1. Ja t<0,5, tad pietiek jau ar trim polinoma
locekļiem, lai dabūtu pareizus pirmos 4 zīmīgos ciparus.
Ir
zināmas arī vairākas citas rindas, kuras lieto, ja t>1, tāpat, ja grib
izskaitļot tieši F(t) vai ievērojot citas īpatnības.
Izmantojot
šīs pašas rindas, jau pagājušajā gadsimtā ir izskaitļotas matemātiskās tabulas,
kas toreiz dažkārt prasīja daudzu gadu ilgu un mokošu darbu.
4.3. Logaritmiski normālā sadalījuma uzdevums
5.
Uzdevums.
Mājsaimniecību
budžetu statistikas novērojumi parādīja, ka vidējais ienākums, rēķinot uz vienu
mājsaimniecības locekli, bija Ls 60
mēnesī ar standartnovirzi 40 lati.
Aprēķināt,
cik procentu mājsaimniecību teorētiski var sagaidīt ar ienākumiem zem 40 latiem
mēnesī un cik procentu - ar ienākumiem virs 130 latiem mēnesī, ja
mājsaimniecību sadalījums pēc ienākumiem atbilst logaritmiski normālā
sadalījuma likumam.
Analīze.
Jau
pēc sākotnējiem datiem ir redzams, ka nevar tieši izmantot normālā sadalījuma
likumu. Atskaitot no vidējā ![]() divkāršu
standartnovirzi 2 ·
40 , iegūstam negatīvu ienākumu, kas no profesionālā viedokļa nav iespējams
(60-80).
divkāršu
standartnovirzi 2 ·
40 , iegūstam negatīvu ienākumu, kas no profesionālā viedokļa nav iespējams
(60-80).
Iedzīvotāju
sadalījums pēc dažādiem dzīves līmeņa rādītājiem bieži veido logaritmiski
normālo sadalījumu, kuram, salīdzinot ar normālo, kreisais zars ir aprauts, bet
labais - izstiepts.
Ja
novērošanas vienības pēc pētītās pazīmes veido logaritmiski normālu sadalījumu,
tās veido normālu sadalījumu pēc šīs pazīmes datu logaritmiem.
Tādēļ
uzdevuma atrisināšanā var izmantot normālā sadalījuma likumu pēc tam, kad ir
atrasts datu logaritmu vidējais, datu logaritmu standratnovirze un logaritmētas
uzdevuma uzrādītās robežvērtības.
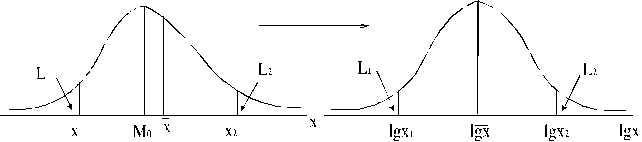
4.24. attēls. Logaritmiski normālā
sadalījuma reducēšana uz normālo sadalījumu gadījumlieluma
variantus (datus) logaritmējot.
Atrisinājums.
1. Ja uzdevumā nav dota datu logaritmu
vidējā vērtība ![]() un datu logaritmu
standartnovirze
un datu logaritmu
standartnovirze ![]() , tās var aprēķināt ar tuvinātām formulām
, tās var aprēķināt ar tuvinātām formulām
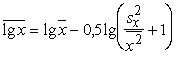 (4.20)
(4.20)
un
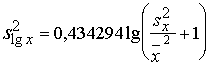 , (4.21)
, (4.21)
Izdarot
vairākus aprēķinus, nācām pie secinājuma, ka pirmā formula dod labu tuvinājumu,
bet otrā diezgan aptuvenu rezultātu. Tādēļ, ja ir iespējams, šie lielumi
jāaprēķina pēc sākotnējiem datiem, tos logaritmējot, atrodot logaritmu vidējo
un standartnovirzi.
Uzdevumā:
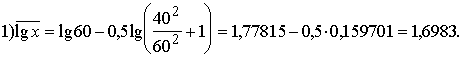
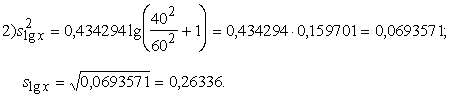
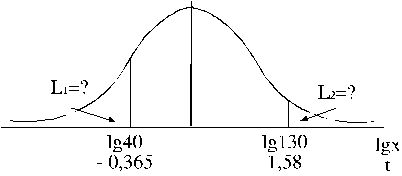
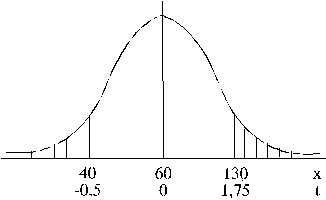
4.25.
attēls. 5. uzdevuma grafiska ilustracija.
2. Ir jāatrod kritisko punktu standartizētās vērtības :
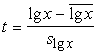 ;
;
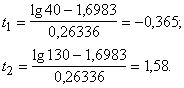
3. Jāatrod attiecīgie integrāļi normālā sadalījuma
tabulās, kas atbilst vajadzīgajām laukuma daļām zem līknes:
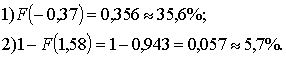
Atrisinājums.
Var vērtēt, ka 36% mājsaimniecību
ienākumi ir bijuši zem Ls 40 mēnesī, rēķinot uz vienu mājsaimniecību locekli,
bet 5-6% mājsaimniecību - virs Ls 130 mēnesī.
Salīdzināšanai -
atrisinājums, pieņemot, ka mājsaimniecību sadalījums pēc ienākuma ir
normāls.
|
|
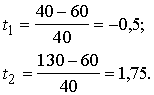
4.26. attēls. 5.
uzdevuma atrisinājums ar normālo
sadalījumu
(rezultāti neprecīzāki)
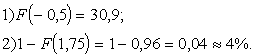
Iznāk
secināt, ka trūcīgo iedzīvotāju ar ienākumu līdz Ls 40 mēnesī īpatsvars jāvērtē
ap 31%. Precīzākais vērtējums pēc logaritmiski normālā sadalījuma ir lielāks -
36%. Savukārt, turīgāko iedzīvotāju īpatsvars ar ienākumu virs 130 Ls mēnesī
pēc normālā sadalījuma iznāk tikai 4%;
precizākais vērtējums pēc logaritmiski normālā sadalījuma - 5-6%.
Tomēr
var sameklēt arī tādus kritiskos punktus, piem., 30 un 100, kur pamatotāks
šķiet vērtējums pēc normālā sadalījuma. Tādēļ vienmēr vajag salīdzināt un
pārbaudīt, kurš no teoretiskajiem sadalījumiem labāk atbilst empīriskajam
kopumā.