Gadījumlielumi un to sadalījumi

3. Gadījumlielumi un to sadalījumi

3.1. Gadījumlielumi un to vispārēji sadalījumi

3.1.1. Pamatjēdzieni un definīcijas

Novērojot gadījumnotikumus, reģistrē alternatīvas atbildes, kuras var izteikt ar ''jā'' un ''nē''. Datoru vajadzībam kodē ar 1 un 0. Elementārs gadījumnotikums var notikt vai nenotikt. Piemēram, kārtējā detaļa var būt derīga vai brāķis. Nekādi starpstāvokļi netiek pieļauti.

Apstrādājot empīrisko novērojumu datus par gadījumnotikumiem, svarīgākais rādītājs, ko aprēķina, ir relatīvais biežums. Varbūtību teorijā kā analogs vispārinošs rādītājs ir varbūtība.

Ja izmēģinājuma vai novērojuma rezultātu fiksē kā skaitli, ko iegūst mērīšanas, svēršanas vai cita instrumenta rādījumu nolasīšanas rezultātā, tad mēs novērojam gadījumlielumu. Katrā atsevišķā novērojumā gadījumlielums iegūst konkrētu, parasti atšķirīgu skaitlisku vērtību, bet daudzos novērojumos tas variē diskrētu vai nepārtrauktu skaitļu apgabalā.

Apstrādājot novērojumu rezultātus par gadījumlielumiem (empīriskos datus), piemēram, datus par mājsaimniecību ienākumiem, tos var grupēt, sastādot empīrisko sadalījuma (variācijas) rindu. Empīrisko sadalījumu vispārinājumi ir teorētiskie sadalījumi jeb gadījumlielumu sadalījumi.

Pēc empīrisko novērojumu datiem aprēķina sadalījuma raksturotājus: aritmētisko vidējo, variācijas rādītājus, retāk - asimetrijas rādītājus. Analogi rādītāji varbūtību teorijā ir matemātiskā cerība (analoga aritmētiskam vidējam), gadījuma lieluma dispersija u.c.

Tā kā empīriskos un teoretiskos sadalījumus saista analoģija, gadījuma lielumu veidi visumā ir analogi statistisko pazīmju veidiem.

Izšķir diskrētus un nepārtrauktus gadījuma lielumus.

Diskrēts ir tāds gadījumlielums, kurš novērojuma gaitā var iegūt tikai zināmas skaitliskas vērtības. Visbiežāk - veselu skaitļu vērtības. Diskrēti lielumi parasti ir visi skaitīšanas rezultāti.

Nepārtraukts ir tāds gadījumlielums, kurš var iegūt visas skaitliskās vērtības kādā ierobežotā vai neierobežotā intervālā. Nepātrauktus gadījumlielumus iegūst mērīšanas un svēršanas rezultātā. Paaugstinot instrumenta precizitāti, var pēc patikas izdalīt jaunas un jaunas iespējamās gadījumlieluma vērtības.

Ierobežots ir tāds gadījumlielums, kurš var iegūt skaitliskas vērtības kādā ierobežotā apgabalā (a, b).

Neierobežots gadījumlielums var iegūt skaitliskas vērtības neierobežotā apgabalā. Apgabals var būt neierobežots vienpusēji ( ); () vai abpusēji ().

Ja runājam par diskrētu gadījumlielumu, tad katra šī lieluma vērtība ir saistīta ar savu varbūtību. Tāpat kā katra diskrēta pazīmes nozīme ar savu relatīvo biežumu.

Ja runājam par nepārtrauktu gadījumlielumu, tad ar noteiktu varbūtību ir saistāmi tikai fiksēti gadījumlieluma vērtību intervāli. Tāpat nepārtrauktām pazīmēm relatīvos biežumus var uzrādīt tikai intervāliem. Viena intervāla ietvaros vismaz teorētiski var izdalīt neierobežoti daudz gadījumlieluma vērtību. Tādēļ katras atsevišķi ņemtas vērtības varbūtība ir nulle.

3.1.2. Gadījumlielumu sadalījumi

Vienkāršāks ir diskrēta gadījumlieluma sadalījums. Par diskrēta gadījuma lieluma sadalījumu sauc likumu, kas saista atsevišķas gadījumlieluma vērtības ar viņu varbūtībām. Šādu likumu, resp., sadalījumu var parādīt tabulas veidā (3.1. tabula).

3.1. tabula

Gadījumlieluma sadalījuma vispārējs pieraksts ar tabulu.



			1

Šādā tabulā visu iespējamo gadījumlieluma vērtību varbūtības ir dotas tieši.

Līdz ar to 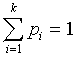, kur k - gadījumlieluma iespējamo vērtību skaits.

Dažreiz sadalījuma likumu var uzrādīt arī ar formulu. Tad jānorāda, kādas darbības jāizdara ar , lai iegūtu , resp. .

Ja gadījumlielums ir nepārtraukts, tad vietā ir jāņem gadījumlieluma intervāli. Tā kā intervālus var izvēlēties dažādus, ar tabulu sadalījuma likumu var atspoguļot tikai tuvināti. Šādā gadījumā ir vēlams, ja tas ir iespējams, sadalījuma likumu uzdot ar formulu.

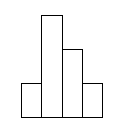
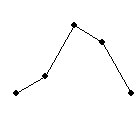
Gadījumlieluma sadalījumus var attēlot grafiski. Empirisko un teorētisko sadalījumu līdzību un atšķirības grafiski var parādīt šādi (3.1. attēls).

Empīriskie

Teorētiskie

Diskrēta gadījuma lieluma sadalījuma attēls ir histogramma vai poligons. Šādi var attēlot arī nepārtraukta gadījumlieluma sadalījumu, uz horizontālās ass atliekot intervālus, bet uz vertikālās - to biežumus

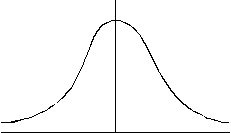
Nepārtraukta gadījumlieluma teorētiskais sadalījums veido laidenu līkni. Var iedomāties, ka intervālu lielums šeit ir neierobežoti mazs. Ja šādu līkni uzdod ar formulu, to sauc par sadalījuma blīvuma funkciju jeb sadalījuma diferenciālo funkciju.

Lai empīriskais un teorētiskais sadalījums būtu salīdzināmi, mērogi uz skalām jāizvēlās tā, lai laukumi zem līknēm būtu vienādi - parasti vienu vienību lieli.

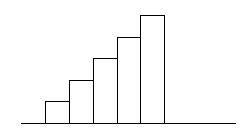
Uzkrāto biežumu sadalījumā katrs stabiņš attēlo atbilstošās vērtības, resp. intervāla un visu iepriekšējo intervālu biežumu summu. Neviens stabiņš nevar būt zemāks par iepriekšējiem. Pēdējais stabiņš reprezentē visu kopas apjomu.

Šādu sadalījumu vizuāli iegūst, izlīdzinot empirisko, uzkrāto biežumu sadalījumu (pa kreisi).

Matemātiski to iegūst, integrējot sadalījuma diferenciālo funkciju (augšā).

Kreisajā zarā līkne asimptotiski tuvojas nullei (abscisu asij), bet labajā zarā, ja biežumi ir standartizēti, - vienam (horizontālai taisnei vienu vienību lielā attālumā no koordinātu sākuma)

3.1. attēls. Sadalījumu veidi ar īsiem paskaidrojumiem.

Matemātiskajā statistikā sadalījuma likumus (teorētiskos sadalījumus) cenšas izteikt ar formulām. Sadalījuma funkcijas var būt vispārējas, kur funkciju parametri ir pierakstīti ar burtiem, un konkrētas, kur sadalījuma parametri ir pierakstīti ar skaitļiem. Vispārējām funkcijām ir teorētiska nozīme. Risinot uzdevumus, ir jāzina konkrētas funkcijas ar skaitliskiem parametriem.

Konkrētās sadalījuma funkcijas var pierakstīt nestandartizētā un standartizēta formā. Nestandartizētā formā funkcijas arguments x atspoguļo novērojuma mērvienības (lati, metri, kilogrami), bet funkcija - absolūtos vai relatīvos biežumus. Standartizētā formā funkcijas argumentu standartizē :

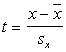, (3.1)

bet funkciju standartizē tā, lai laukums zem līknes būtu vienu vienību liels.

Dažādus aprēķinus vieglāk izdarīt ar standartizēto gadījumlielumu sadalījumiem, jo viņu funkcijas ir vienkāršākas. Tās iespējams tabulēt, kamēr nestandartizēto funkciju skaits ir neierobežots.

Konkrētā pētījumā pēc statistikas datiem bieži vieglāk aprēķināt sadalījuma diferenciālo funkciju. Sākotnēji vieglāk arī to izprast.

Vispārīgā veidā vieglāk definēt integrālo funkciju, un nereti ar to vieglāk izpildīt nepieciešamās darbības.

3.1.3. Sadalījumu funkcijas

Vispārējo gadījumlielumu kā mainīgu lielumu parasti apzīmē ar kādu lielo alfabeta beigu burtu, visbiežāk ar X. Noteiktu šī lieluma vērtību, piemēram, kādu robežvērtību, apzīmē ar attiecīgo mazo burtu x, bet, ja ir vajadzīgs, norādīt vairākas vērtības, tam pievieno skaitliskus indeksus utt. Dažos gadījumos izmanto alfabeta sākuma burtus: a,b,c.

Varbūtību, ka gadījuma lielums X ir mazāks par kādu robežvērtību x, apzīmē ar simbolu , jo šī varbūtība ir atkarīga tikai no uzdotās robežvērtības. Tātad

. (3.2)

Funkciju sauc par gadījuma lieluma sadalījuma integrālo funkciju. Tas ir pavisam abstrakts pieraksts. Konkrētā uzdevumā ir jāatklāj, kādas darbības apzīmē funkcijas simbols F, resp., kādas darbības jāizdara ar x, lai iegūtu varbūtību F(x). Citā vispārējā pierakstā

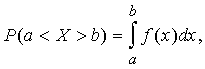(3.2a)

kur : P - varbūtība, ka gadījumlielums nonāks intervālā [a,b];

- gadījumlieluma sadalījuma funkcija.

Ja gadījumlielums X ir diskrēts un tā neuzkrāto lielumu sadalījums ir dots ar tabulu, tad F(x) atrašana nozīmē summēt visu to gadījumlieluma vērtību, kas mazākas par x, varbūtības. Pieskaitot kārtējo varbūtību, F(x) izmainās lēcienveidīgi.

Grafiski to var parādīt šādi (3.2. attēls)

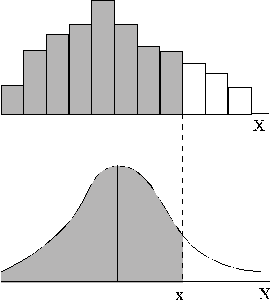
3.2. attēls. Gadījumlieluma varbūtību summēšana no sadalījuma
kreisā zara līdz kritiskai vērtībai, izmantojot vienkāršos sadalījumus.

Ja gadījumlielums ir nepārtraukts, summēšana nav iespējama un tā jāaizstāj ar integrēšanu. Saprotot noteikto integrāli kā laukuma daļu zem līknes, šī darbība grafiski parādīta 3.2. attēlā apakšējā daļā.

Tā kā praksē daudz biežāk iznāk strādāt ar nepārtrauktiem, nekā ar diskrētiem gadījumlielumiem, no šejienes nāk vispārējais nosaukums: sadalījuma integrālā funkcija.

Integrālo sadalījuma funkciju grafiski var attēlot, arī tieši atliekot F(x) uz ordinātu ass. Tad attēli ir šādi. (3.3. attēls).

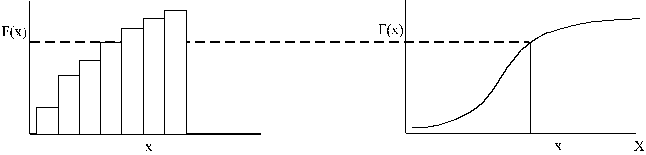
Diskrēts sadalījums Nepātraukts sadalījums

3.3. attēls. Integrālās funkcijas grafiki diskrētam sadalījumam (nosacīti) un nepārtrauktam
sadalījumam.

No integrālās funkcijas jēdziena izriet dažas šīs funkcijas pašas vispārīgākās īpašības.

1. Sadalījuma integrālā funkcija ir varbūtība, tādēļ tā vienmēr ir pozitīvs skaitlis.

2. Ņemot vērā, ka varbūtība nav mazāka par nulli un nav lielāka par vienu, arī

par F(x) var teikt, ka tā vienmēr atrodas šajās robežās:

. (3.3)

3. Funkcija F(x) aug visā definicijas apgabalā, tādēļ, ja , tad

4. Ja gadījuma lielums ir abpusēji neierobežots, tad integrālās funkcijas zemākā robežvērtība 0 tiek sasniegta, kad , bet augstākā robežvērtība

1, kad . Ja gadījuma lielums ir vienpusēji vai abpusēji ierobežots,

uzrādītās robežvērtības F(x) iegūst, x sasniedzot savas robežvērtības.

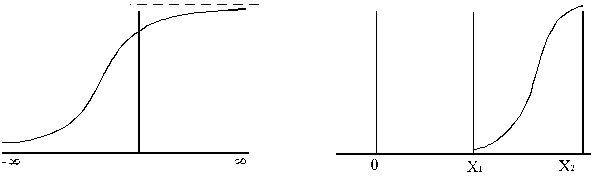
x abpusēji neierobežots x abpusēji ierobežots

3.3. attēls. Integrālās funkcijas definīcijas apgabali.

Gadījumlieluma diferenciālo funkciju definē tāpat kā jebkuras funkcijas atvasinājumu:

. (3.4)

Tātad tā ir funkcijas F(x) pieauguma attiecība pret argumenta x pieaugumu, ja pēdējais tiecas uz nulli.

Ja ir dota sadalījuma integrālā funkcija, diferenciālo funkciju atrod kā integrālās funkcijas pirmo atvasināto. Ja ir dota diferenciālā funkcija, integrālo funkciju atrod, integrējot doto funkciju.

Gadījumlieluma diferencialo funkciju sauc arī par sadalījuma blīvuma funkciju.

Par empiriskā sadalījuma blīvumu sauc kopas vienību skaitu uz vienu vienību lielu argumenta x intervālu. Tā kā, izdarot grupēšanu, intevālu lielumi gandrīz vienmēr ir lielāki par 1, intervālu blīvumus atrod, kopas vienību skaitu intervālā dalot ar intervāla lielumu (garumu).

Teorētiskais gadījuma lieluma sadalījums ir robeža, uz kuru tiektos empiriskais sadalījums, ja neierobežoti palielinātu izdalāmo grupu skaitu, vienlaikus samazinot grupēšanas intervālu lielumus

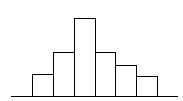
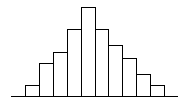
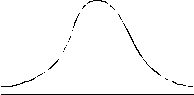
3.5. attēls. Teorētiskais sadalījums kā empīriskā sadalījuma robeža.

Skalas jāizvēlās tā, lai kopējie laukumi visos attēlos būtu vienādi.

Ir skaidrs, ka, ievērojami palielinot grupu skaitu, vienu vienību liels intervāls ir lielāks nekā sākotnējie intervāli; robežgadījumā tas ir neierobežoti lielāks.

Turklāt teorētiskos sadalījumus veido tā, lai laukums zem līknes atbilstu nevis kopas vienību skaitam, bet būtu vienu vienību liels (droši sagaidāma notikuma varbūtība). Tādēļ sadalījuma diferenciālās funkcijas statistiskā interpretācija iznāk sarežģītāka.

Vienkāršāk sadalījuma diferenciālās funkcijas lielumus iztēloties kā sadalījuma diferenciālās funckijas līknes augstumus virs abscisu ass.

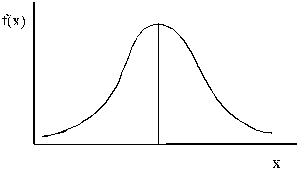
3.6. attēls. Gadījumlieluma diferenciālā funkcija.

Gadījumlieluma diferenciālai funkcijai ir šādas svarīgākās īpašības.

1. Funkcija var būt tikai pozitīvs skaitlis, bet aiz sadalījuma eksistences robežām

nulle:

Līkne grafiskajā attēlā vienmēr atrodas virs abscisu ass.

2. Tā kā runa ir par varbūtību sadalījumu, laukums, ko ierobežo līkne un abscisu ass, ir vienu vienību liels. Tas ir nepieciešami, jo gadījuma lielumam novērojuma rezultātā noteikti jāiegūst kāda vērtība teorētiski iespējamā variācijas apgabalā. Un šo iespējamo x vērtību varbūtību summa ir viens.

Tāpat arī empīriskā statistikā visu relatīvo biežumu summa ir viens, ja relatīvos biežumus izsaka viena daļās.

3.1.4. Gadījumlieluma raksturotāji

Gadījuma lieluma īpašības vispilnīgāk izsaka sadalījuma funkcijas. Koncentrētāk tās izsaka sadalījuma vispārinošie rādītāji, kuri nav funkcijas, bet ir konkrēti skaitļi.

Arī šeit gadījuma lielumam ir analoģija ar statistisko pazīmi.

Statistisko pazīmi un tās empīrisko sadalījumu vispirms raksturo centrālās tendences rādītāji, to vidū svarīgākais ir pazīmes aritmētiskais vidējais. Runājot par gadījumlieluma sadalījumu (teorētisko sadalījumu), tā centrālo tendenci raksturo matemātiskā cerība. Citi autori arī to sauc par gadījumlieluma aritmetisko vidējo.

Diskretam sadalījumam matemātisko cerību (aritmētisko vidējo) var aprēķināt, izdarot elementāras darbības

, (3.5)

kur - gadījumlieluma vērtības,

- šo vērtību varbūtības.

Matemātiskai cerībai, tāpat kā aritmetiskam vidējam, ir tas pats saturs, kas sākotnējiem datiem, un tā pati mērvienība.

Iepriekšējā formula no aritmetiskā vidējā formulas atšķiras ar to, ka par statistiskajiem svariem ir izmantotas varbūtības , nevis absolūtie var relatīvie biežumi . Bez tam nav vajadzīgs parādīt dalīšanu ar svaru summu, jo tā šajā gadījumā vienmēr ir viens: .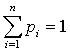

Ja gadījuma lielums ir nepārtraukts, tad viņa matemātisko cerību šādi aprēķināt nevar, jo būtu jāsaskaita neierobežots skaits reizinājumu . Tādēl, tieša summēšana ir jāaizstāj ar integrēšanu.

Nepārtraukta gadījumlieluma matemātiskās cerības vispārējā formula ir šāda:

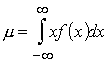, (3.6)

kur x - gadījuma lielums,

f(x) - tā diferenciālā sadalījuma funkcija.

Lai formulu varētu izmantot praktiski, simbola f(x) vietā ir jāievieto konkrēta sadalījuma diferenciālā funkcija. Tālāk var izdarīt integrēšanas darbības.

Plašāk izmantotajiem sadalījumiem nepieciešamie integrāļi ir atrasti un tos var izmantot gatavā veidā.

Gadījumlieluma variāciju raksturo tā dispersija. Gadījumlieluma dispersija arī ir analoga parastai statistiskās pazīmes dispersijai.

Diskrēta gadījumlieluma dispersiju definē šādi:

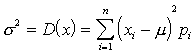, (3.7)

kur

- matemātiskā cerība; citi simboli labajā pusē ir iepriekšējie.

Formulā par statistiskajiem svariem izmanto varbūtības , aritmētiskā vidējā vietā nāk matemātiskā cerība un nav jāparāda dalīšana ar varbūtību (svaru) summu, jo tā ir viens.

Iepriekšējo formulu var pārveidot arī t.s. momentu formulas formā:

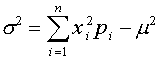, (3.8)

kura ir ērtāka izskaitļojumiem, bet neatklāj dispersijas būtību.

Nepārtraukta gadījuma lieluma dispersija, tāpat kā matemātiskā cerība, ir jāaprēķina, izmantojot integrāli. Definīcijas formula ir šāda:

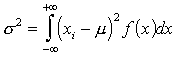, (3.9)

bet izskaitļojumiem ērtāka ir momentu formula

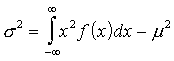(3.10)

Kvadrātsakne no gadījuma lieluma dispersijas ir gadījuma lieluma standartnovirze.

Matemātiskās cerības īpašības ir analogas aritmētiskā vidējā īpašībām, bet gadījumlieluma dispersijas īpašības - parastās empīriskās dispersijas īpašībām. Tādēļ viņas neatkārtosim.

Teorētiskajiem sadalījumiem piemīt arī asimetrija un ekscess. Virknei biežāk lietoto teorētisko sadalījumu asimetrijas un ekscesa rādītāji ir skaitliskas konstantes.

Tās ir atrastas, matemātiski izpētot attiecīgo sadalījumu funkcijas. Praktiski tās atrod rokasgrāmātās bez ikreizējas aprēķināšanas.

3.2. Vienmērīgs sadalījums

3.2.1. Vienmērīga sadalījuma funkcijas

Par vienmērīgu sadalījumu jeb sadalījumu ar konstantu blīvumu sauc tādu sadalījumu, kur gadījumlieluma vērtības ir abpusēji ierobežotas un ierobežotā apgabala ietvaros vienādi varbūtīgas.

Ja gadījumlielums x ir sadalīts vienmērīgi intervālā [a; b], tad varbūtību blīvums f(x) ārpus šī intervāla ir nulle, bet intervāla ietvaros ir konstante:

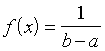. (3.11)

Vienmērīga sadalījuma diferenciālās funkcijas grafiskais attēls ir taisnstūris. (3.7. attēls)

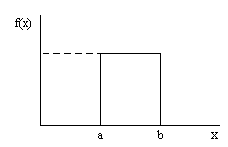
3.7. attēls. Vienmērīga teorētiskā sadalījuma diferenciālās funkcijas attēls.

Analogs empīriskais sadalījums parādītu vienāda augstuma stabiņus histogrammā.
(3.8. attēls)

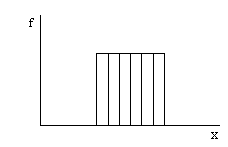
3.8. attēls. Vienmērīga empīriskā sadalījuma attēls.

Vienmērīgs sadalījums no matemātiskā viedokļa ir pats vienkāršākais teorētiskais sadalījums. Tādēļ to parasti izmanto, demonstrējot darbības ar sadalījumiem un to raksturotājiem.

Vienmērīga sadalījuma praktiskas lietošanas iespējas ir niecīgas. Vismaz ekonomikā tam grūti atrast pielietojumu.

Vienmērīga sadalījuma integrālo funkciju var pierakstīt šādi:

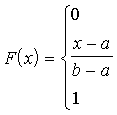
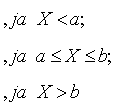(3.12)

Attēlu veido trīs taisnes nogriežņi, skat. 3.9. attēlu.

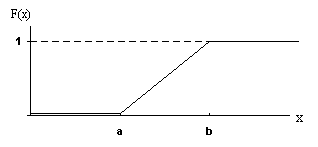
3.9. attēls. Vienmērīga sadalījuma integrālās funkcijas attēls.

Tālāk ar vienmērīgu gadījumlielumu sadalījumu iepazīsimies, izmantojot skaitlisku piemēru.

Piemērs. Dota gadījumlieluma X integrālā funkcija:

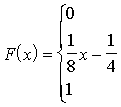
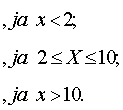
Uzzīmēt šīs funkcijas grafisko attēlu, atrast diferenciālo funkciju (sadalījuma blīvuma funkciju), uzzīmēt šīs funkcijas grafisko attēlu, pārliecināties, ka funkcija ir vienmērīga sadalījuma funkcija.

Analīze un atrisinājums.

Funkcijas F(x) grafiskais attēls inetrvālā ir horizontāla taisne, kas sakrīt ar abscisu asi, bet intervālā - horizontāla taisne, paralēla abscisu asij, vienu vienību lielā attālumā no tās. Intervālā (2; 10) funkcija F(x) ir lineāra, jo tās vienādojums ir

Tāda vienādojuma grafiks ir taisne.

Piezīme: Lineāru vienādojumu var pierakstīt arī tādā formā, ka tas nesakrīt ar parasto lineāra vienādojuma pierakstu:

Vienādojums joprojām ir lineārs.

Savienojot punktus (2;0) un (10; 1) ar taisni, pabeidzam attēla izveidošanu.

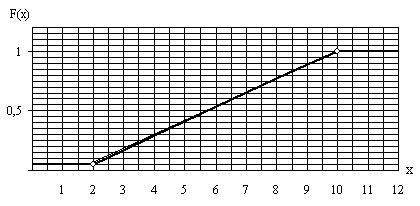
3.10. attēls. Vienmērīga sadalījuma integrālā funkcija (grafiks metriskā skalā)

Funkcijas interesantākais apgabals ir .

Pārliecināmies, vai dotā funkcija atbilst vienmērīgas funkcijas definīcijai (3.12.), ievietojot a=2 un b=10 definīcijas formulā

Definīcijas prasības ir izpildītas. Tātad dotā sadalījuma funkcija patiešām ir vienmērīga sadalījuma funkcija. Vēl var pārliecināties, ka līnijas lūzuma punktos ir vajadzīgās integrālās funkcijas vērtības

Lai atrastu diferenciālo funkciju pēc integrālās, ir jāatrod integrālās funkcijas pirmā atvasinātā.

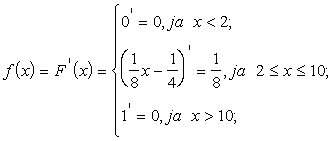
Interesantākajā definīcijas apgabala daļā diferenciālā funkcija ir konstante

Pārbaudām, vai iegūtais rezultāts atbilst vienmērīga sadalījuma diferenciālās funkcijas definīcijai (3.11) :

Tātad aprēķini ir izdarīti pareizi. Uzzīmējam diferenciālo sadalījuma funkciju. Tās attēls ir taisnstūris, kura augstums ir 1/8. Viņa laukums ir vienu vienību liels:

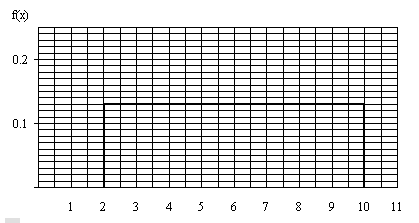
3.11. attēls. Vienmērīga sadalījuma diferenciālā funkcija (grafiks metriskā skalā)

Izveidojam un atrisinam pretēju uzdevumu. Pieņemam, ka ir dota diferenciālā funkcija

apgabalā [2;10].

Lai atrastu integrālo funkciju, diferenciālā funkcija ir jāintegrē, pēc dx:

Skaitli C var atrast, ievietojot tikko atrastajā integrālajā funkcijā kādu argumenta robežvērtību un tai atbilstošo integrālo funkciju. Piemēram, ja x=2, tad F(x) = 0.

Līdz ar to ; tātad un ,

kas atbilst sākotnējam uzdevumam.

3.2.2. Vienmērīga sadalījuma matemātiskā cerība un dispersija

Izvirzām uzdevumu aprēķināt matemātisko cerību sadalījumam

intervālā [2; 10].

Var izmantot vispārējo formulu

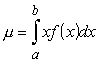, (3.13)

kura neprasa norādi, ka sadalījums ir vienmērīgs.

Ievietojot ; a = 2; b = 10, iegūstam

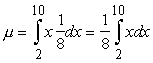To integrējam kā pakāpes funkciju, ievērojot, ka

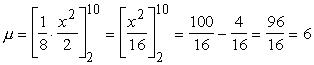
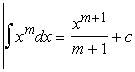
Ja papildus dotajam zinām, ka sadalījums ir vienmērīgs, matemātisko cerību var aprēķināt ar speciālo formulu, kura ir daudz vienkāršāka:

. (3.14)

Piemērā

Ja sadalījums ir vienmērīgs, matemātiskā cerība (aritmētiskais vidējais) sakrīt ar variācijas apgabala centru, kas, aplūkojot grafisko attēlu, ir visai pārliecinoši.

3.12. attēls. Vienmērīga sadalījuma matemātiskā cerība

Vienmērīga sadalījuma dispersiju arī var aprēķināt ar vispārējo un speciālo formulu. Izvēlotiers vispārējo formulu, ērtāk strādāt ar tās momentu formu

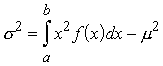. (3.15)

Ievietojot , iegūstam

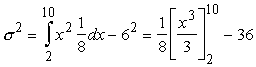(integrējam pēc pakāpes integrāla formulas)

Standartnovirze .

Ja ir zināms, ka sadalījums ir vienmērīgs, to pašu rezultātu var iegūt daudz vienkāršāk, lietojot speciālo formulu:

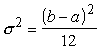. (3.16)

Ievietojot iegūstam

3.2.3. Empīriska pārbaude

Vienmērīga sadalījuma dispersijas jēgu var padziļināt, vēlreiz to izrēķinot ar empīriskās statistikas metodēm. Šajā nolūkā diferenciālā sadalījuma taisnstūra vietā ņemam histogrammu ar pietiekami šauriem stabiņiem un to viduspunktiem izrēķinām dispersiju.

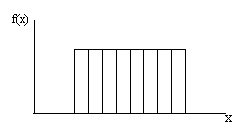
3.13. attēls. Vienmērīga sadalījuma empīrisks analogs -
histogramma ar vienāda augstuma stabiņiem.

Iegūtā atbilde būs tuva iepriekš iegūtai teorētiskā sadalījuma dispersijai, bet ar to nesakrītis, jo grupēšanas rezultātā zaudējam iekšgrupu dispersiju.

Sadalām intervālu [2; 10] astoņās vienādās daļās; intervāli ir vienu vienību lieli un to statistiskie svari vienādi. Tādēļ varam rēķināt vienkāršo dispersiju. Izmantojam momentu formulu.

3.2. tabula
Piemēra starprezultāti.


		2,5	6,25
		3,5	12,25
		4,5	20,25
		5,5	30,25
		6,5	42,25
		7,5	56,25
		8,5	72,25
		9,5	90,25
			330

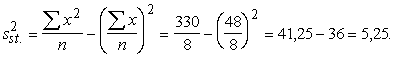Teorētiskie aprēķini deva .

5,25 ir starpgrupu dispersija. Ja sadalījums ir vienmērīgs, tad iekšgrupu dispersiju var novērtēt ka no intervāla lieluma kvadrāta

. (3.17)

Piemērā

un , (3.18)

piemērā

kas sakrīt ar iepriekšējo.

Piezīme. Vienmērīga sadalījuma iekšgrupu dispersijas formulu nedrīkst jaukt ar t.s. Šeparda labojumu, ar kura formu ir vizuāla līdzība. Šeparda labojuma formula ir

kura domāta nevis vienmērīgam, bet normālam sadalījumam.

3.3. Binomiālais sadalījums

3.3.1. Definīcija un īpašības

Ar binomiālo sadalījumu sastopamies, ja ir jānovērtē atkārtotu novērojumu varbūtības. Turklāt katrā novērojumā tiek fiksēta alternātīva atbilde: ''jā'' vai ''nē''. Tātad katra novērojuma gaitā novērojam gadījumnotikumu kurš var notikt un var nenotikt. Bet, ja novērojumu izdara n reizes, tad par kopējo rezultātu vairs nevar atbildēt ar ''jā'' vai ''nē''. Viegli saprast, ka n novērojumos varam konstatēt notikuma iestāšanos jeb atbildi ''jā'' n reizes, n-1 reizi . . . m reizes . . . 1 reizi, 0 reizes.

Varbūtību, ka notikums notiks m reizes, var aprēķināt ar Bernulli formulu.

Tā kā binomiālais sadalījums ir diskrēta gadījuma lieluma sadalījums, to var uzradīt tieši tabulas veidā. Šajā nolūkā tabulas pirmajā ailē uzrāda visus gadījumlieluma m variantus, tātad skaitļus n, n-1; n-2; ...; 1; 0. Otrajā ailē uzrāda viņu varbūtības kā Ņūtona binoma (p+q)ⁿ izvirzījuma locekļus. Lieluma m variantus var sakārtot arī pretējā secībā: 0; 1; 2; ...n. Tad attiecīgās varbūtības būs binoma (q + p)ⁿ izvirzijuma locekļi.

Šāda tabula ir binomiālais sadalījums un pēc savām īpašībām atgādina citu sadalījumu diferenciālo funkciju.

Binomiālā sadalījuma integrālo funkciju šaurā nozīmē (izmantojot integrēšanas darbību) nelieto. Tā kā gadījumlielums ir diskrēts, visu uzdevuma nosacījumiem atbistošo m vērtību varbūtības var tieši saskaitīt, izveidojot kumulatīvo varbūtību sadalījuma rindu. Tā būs sadalījuma integrālā funkcija, saprotot terminu plašā nozīmē.

Binomiālā sadalījuma (neuzkrātā) grafiskais attēls ir poligons (skat. 3.14. attēlu).

Binomiālā sadalījuma piemērs.

Loterijas rīkotāji saviem pircējiem apgalvo, ka katra desmitā loze laimē. Pieņemot, ka viņi laimes ratā izlozei patiešām ievieto 10% ''pilnas'' un 90% ''tukšas'' biļetes, aprēķināt, kāda varbūtība pircējam, kas nopērk tieši 10 lozes:

1. laimēt vispār,

2. laimēt tieši vienu laimestu,

3. laimēt trīs vai vairāk laimestus.

Analīze un atrisinājums.

Var rasties kļūdaina doma, ka, pērkot desmit lozes, vismaz vienai noteikti jālaimē. Tas nav pareizi.

Pieņemot vienas lozes laimestu par labvēlīgu notikumu, tā notikšanas varbūtība ir p = 0,1; pretēja notikuma varbūtība q = 0,9.

Uzdevuma pirmo jautājumu var atrisināt, izmantojot vismaz viena vēlama notikuma notikšanas varbūtības formulu:

Varbūtība atspoguļo iespēju laimēt ar vienu, divām, ..., visām desmit lozēm.

Uzdevuma pēdējā jautājuma atrisināšana ir nedaudz sarežģītāka, tādēļ mācību nolūkos izveidosim visu binomialo sadalījumu

kas atspoguļo šīs spēles situāciju.

3.3 tabula

Piemēra starprezultāti.

0,348678

0,1

0,387420

0,01

0,430467

0,193710

120

0,001

0,478297

0,057396

210

0,0001

0,531441

0,011160

252

1.10^-5

0,590490

0,001488

0,070191

6

210

1.10^-6

0,656100

0,000138

120

1.10^-7

0,729000

0,000009

1.10^-8

0,810000

0,000000

1.10^-9

0,900000

0,000000

1.10^-10

1,000000

0,000000

0,999999=1

Tabulas piektās ailes otrā rindā var tieši nolasīt, ka, pērkot 10 lozes, varbūtība iegūt vienu laimestu ir 0,387.

Lai iegūtu trešā jautājuma atbildi - varbūtību iegūt trīs vai vairāk laimestus - ir jāsaskaita piektās ailes pēdējās 8 rindās uzrādītās varbūtības. Iegūstam 0,070.

Lai iegūtu pirmā jautājuma atbildi, būtu jāsaskaita piektās ailes visas varbūtības, atskaitot pirmo. Vieglāk ir atskaitīt no viena pirmo varbūtību, ko aprēķinājam jau agrāk.

Pārskatot tabulas pēdējo aili kopumā, redzam, ka vislielākā varbūtība ir , gandrīz tikpat liela ir varbūtība . Sākot ar varbūtības ir ļoti mazas un asimptotiski dilstošas.

Visu varbūtību summa, ja neskaita noapaļošanas kļūdu, ir viens.

Tabulas pirmā un pēdējā aile atspoguļo binomiālo sadalījumu 3.14. attēlā šis sadalījums ir parādīts kā pirmā lauztā līnija.

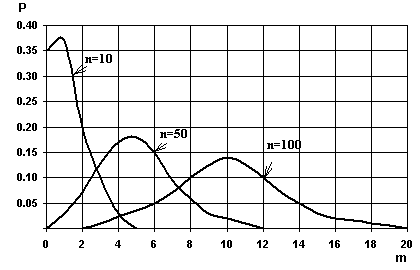
3.14. attēls. Binomālā sadalījuma poligoni.

Iepriekšējā grafiskā attēlā ir parādīti binoma poligoni, ja n=10; 50; 100.

3.3.2. Binomiālā sadalījuma raksturotāji

Binomiālajam sadalījumam, kā jebkuram sadalījumam, ir iespējams aprēķināt svarīgakos raksturotājlielumus.

Binomiālā sadalījuma matemātisko cerību jeb vienkārši vidējo lielumu aprēķina ar formulu

, (3.19)

kur

p - gadījuma notikuma notikšanas varbūtība vienā novērojumā; visos novērojumos tā ir vienāda;

n - novērojumu skaits.

Matematiskā cerība var iznākt arī daļskaitlis. Ja uzdevuma interpretācija nepieļauj daļskaitli, jāņēm tuvākā vesela skaitļa vērtība.

Piemērā .

Šis lielums ir vēlamā notikuma notikšanas reižu skaits m dotajos 10 izmēģinājumos, kura varbūtība ir vislielākā. Par to viegli pārliecināties iepriekšēja tabulā.

Grafiskajā attēlā ir abscisa, pret kuru paceļas sadalījuma poligona virsotne.

Binomiālā sadalījumā dispersija ir:

, (3.20)

bet standartnovirze:

. (3.21)

Piemērā

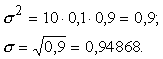
Binomiāla sadalījuma dispersija ir proporcionāla novērojumu skaitam atkārtotu novērojumu sērijā n.

Pieaugot novērojumu sēriju lielumam, binomiālā sadalījuma variācijas rādītāji strauji pieaug.

Piezīme.

Šos rādītājus nedrīkst jaukt ar alternatīvas pazīmes standartnovirzi vaitāpat ar relatīvā biežuma standartkļūdu izlases metodē.

Binomiālā sadalījuma asimetrijas koeficients ir

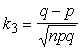. (3.22)

3.3.3. Binomiālā sadalījuma robeža.

Aplūkosim, kas notiek, ja nemainīgos apstākļos, saglabājoties varbūtību p un q vērtībām, palielina novērojumu skaitu.

Iepriekšējā piemērā varbūtība laimēt ar katru nopirkto lozi bija 0,1. Iedomāsimies, ka pērkam nevis 10, bet 50; 100 un 1000 lozes. Visvarbūtīgāko laimestu skaitu katrā gadījumā aprēķina ar matemātiskas cerības formulu. Piemēram, pērkot 50 lozes, vislielākā varbūtība būs laimēt , pērkot 100 lozes - 10 - reizes utt. Bet šo matemātisko cerību varbūtības arvien samazinās. Tās aprēķina ar Bernulli formulu, vai Laplasa formulu, kas dod tuvinātu rezultātu, Skat. 3.4 tabulu.

3.4 tabula

Piemēra tuvināti aprēķini.

n
10	1	0,3874
50	5	0,1849
100	10	0.1319
1000	100	0,0421

Secinājumi.

1. Ja novērojumu skaitu n palielina, iespējamo m vērtību (variantu) skaits pieaug. Līdz ar to samazinās katras atsevišķi ņemtas m vērtības varbūtība. Arī tās m vērtības, kuras varbūtība ir vislielākā. (Varbūtību summa 1 jāsadala arvien vairāk daļās).

2. Līdz ar n pieaugumu samazinās interese par to, ka n izmēģinājumos notikums notiks tieši m reizes. Piemēram no 1000 izmēģinājumiem tieši 937 reizes. Šādos gadījumos praktiska interese ir par varbūtību, ka m atradīsies zināmā intervālā. piemēram no 900 - 1000.

3. Ja novērojumu skaits ir liels, intervāla, kurā sagaidām m, varbūtības aprēķinašana ar Bernulli formulu kļūst ļoti darbietilpīga. Lietojot šo metodi, būtu jāsummē vairāki desmiti un pat simti vai tūkstoši varbūtību, no kurām katra prasa samērā lielu skaitļošanas darbu.

4. Tādēļ, ja n ir liels skaitlis (praktiski jau virs 30...50), uzskata, ka diskrēto gadījuma lielumu var aizstāt ar nepārtrauktu gadījumlielumu un diskrēto binomiālo sadalījumu ar nepārtraukta gadījuma lieluma sadalījumu, kuram asimptotiski tuvojas binomiālais sadalījums, ja neierobežoti palielina n. Ir pierādīts, ka parastā gadījumā tāda binomiālā sadalījuma robeža ir normālais sadalījums (speciālā gadījumā - Puasona sadalījums). Par to var pārliecināties 3.14. attēlā.

5. Binomiālā sadalījuma aizstāšana ar normālo, ja n ir liels, dod pietiekami labus tuvinātus rezultātus, ievērojami samazinot skaitļošanas darbu.

6. Normālā sadalījuma lietošana binomiālā sadalījuma vietā ir tikai viena uzdevumu klase, kur lieto normālo sadalījumu. Normālam sadalījumam ir liela patstāvīga nozīme. Viņš nav saistāms ar binomiālo sadalījumu, ja gadījuma lielums jau pēc savas dabas ir nepārtraukts. Tad gadījuma lielumi katra atsevišķa novērojuma rezultātā var iegūt jebkuras skaitliskas vērtības ierobežotā vai neierobežotā intervālā.

Kādos reālos nosacījumos gadījuma lielums veido normālo sadalījumu, precīzē Ļapunova teorēma.

Normālam sadalījumam būs veltīta turpmākā nodaļa.